人教新课标高中数学必修5 第三章不等式 3.1不等关系与不等式同步测试

试卷更新日期：2017-01-12 类型：同步测试

进入出卷网下载

一、单选题

1. 有三个房间需要粉刷，粉刷方案要求：每个房间只用一种颜色，且三个房间颜色各不相同．已知三个房间的粉刷面积（单位：m²）分别为x，y，z，且x $<$ y $<$ z，三种颜色涂料的粉刷费用（单位：元/m²）分别为a，b，c，且a $<$ b $<$ c，在不同的方案中，最低的总费用（单位：元）是（）

A、ax+by+cz B、az+by+cx C、ay+bz+cx D、ay+bx+cz

查看试题解析
2. 若a＞b＞0，c＜d＜0，则一定有（　　）

A、 $\frac{a}{c}$ ﹣ $\frac{b}{d}$ ＞0 B、 $\frac{a}{c}$ ﹣ $\frac{b}{d}$ ＜0 C、 $\frac{a}{d}$ ＞ $\frac{b}{c}$ D、 $\frac{a}{d}$ ＜ $\frac{b}{c}$

查看试题解析
3. 设 $a < b < 0$ ，则下列不等式中不能成立的是（）

A、 $\frac{1}{a} > \frac{1}{b}$ B、 $\frac{1}{a - b} > \frac{1}{a}$ C、 $|a| > |b|$ D、 $a^{2} > b^{2}$

查看试题解析
4. 若 $a < b < 0$ ，则下列不等式不成立的是（）

A、 $|a| > |b|$ B、 $\frac{1}{a} > \frac{1}{b}$ C、 $a^{3} < b^{3}$ D、 $\frac{1}{a - b} > \frac{1}{a}$

查看试题解析
5. 若a＞b，则下列不等式正确的是（）

A、 B、a³＞b³ C、a²＞b² D、a＞|b|

查看试题解析
6. 已知实数 $a ， b ， c$ 满足 $c < b < a$ ，且 $a c < 0$ ，那么下列不等式一定成立的是（）

A、 $a c (a - c) > 0$ B、 $c (b - a) < 0$ C、 $c b^{2} < a b^{2}$ D、 $a b > a c$

查看试题解析
7. a∈R，且a²＋a＜0，那么－a，－a³ ， a²的大小关系是(　　)

A、 $a^{2}$ ＞－ $a^{3}$ ＞－a B、－a＞ $a^{2}$ ＞－ $a^{3}$ C、－ $a^{3}$ ＞ $a^{2}$ ＞－a D、 $a^{2}$ ＞－a＞－ $a^{3}$

查看试题解析
8. 设 $a > 1 > b > - 1$ ，则下列不等式中恒成立的是 ( )

A、 $a > b^{2}$ B、 $\frac{1}{a} > \frac{1}{b}$ C、 $\frac{1}{a} < \frac{1}{b}$ D、 $a^{2} > 2 b$

查看试题解析
9. 若 $a ， b ， c \in R$ ，且 $a > b$ ，则下列不等式中一定成立的是（）

A、 $\frac{1}{a} < \frac{1}{b}$ B、 $a c > b c$ C、 $\frac{c^{2}}{a - b} > 0$ D、 $(a - b) c^{2} \geq 0$

查看试题解析
10. 如果a＜0，b＞0，那么，下列不等式中正确的是（）

A、 B、 C、a²＜b² D、|a|＞|b|

查看试题解析
11. 设a＜b＜0，则下列不等式中不成立的是（）

A、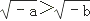 $\frac{1}{a} > \frac{1}{b}$ B、 C、|a|＞﹣b D、

查看试题解析
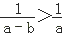12. 如果a＜b＜0，那么下列不等式成立的是（　　）

A、﹣ $\frac{1}{a}$ ＜﹣ $\frac{1}{b}$ B、ab＜b² C、﹣ab＜﹣a² D、|a|＜|b|

查看试题解析
13. 若a＞b，x＞y，下列不等式不正确的是（　　）

A、a+x＞b+y B、y﹣a＜x﹣b C、|a|x≥|a|y D、（a﹣b）x＞（a﹣b）y

查看试题解析
14. 若a、b、c∈R，a＞b，则下列不等式成立的是（　　）

A、 $\frac{1}{a} < \frac{1}{b}$ B、a²＞b² C、a（c²+1）＞b（c²+1） D、a|c|＞b|c|

查看试题解析
15. 如果a＞b＞0，那么下列不等式中不正确的是（　　）

A、 $\frac{1}{a} < \frac{1}{b}$ B、 $\frac{1}{a} > \frac{1}{b}$ C、ab＞b² D、a²＞ab

查看试题解析

二、填空题

16. b克糖水中有a克糖（b＞a＞0），若再加入m克糖（m＞0），则糖水更甜了，将这个事实用一个不等式表示为

查看试题解析
17. 已知﹣1＜a，b，c＜1，比较ab+bc+ca与﹣1的大小关系为．（填“＜”或“=”或“＞”）．

查看试题解析
18. 已知实数a＞b，当a、b满足条件时，不等式 $\frac{1}{a}$ ＜ $\frac{1}{b}$ 成立．

查看试题解析
19. 设a，b是两个实数，给出下列条件：
①a+b＞1；②a+b=2；③a+b＞2；④a²+b²＞2；⑤ab＞1．
其中能推出：“a，b中至少有一个大于1”的条件是．（填序号，只有一个正确选项）

查看试题解析
20. 已知a＞b，ab≠0，则下列不等式中：①a²＞b²；② $\frac{1}{a} < \frac{1}{b}$ ；③a³＞b³；④a²+b²＞2ab，恒成立的不等式的个数是

查看试题解析

三、解答题

21. 表示下列不等关系
（1）a是正数
（2）a+b是非负数
（3）a小于3，但不小于﹣1
（4）a与b的差的绝对值不大于5．

查看试题解析
22. 已知a，b∈R，x=a³﹣b，y=a²b﹣a，试比较x与y的大小．

查看试题解析
23. （1）当x＞1时，比较x³与x²﹣x+1的大小
（2）已知：a＜b， $\frac{1}{a} < \frac{1}{b}$ ．判定a，b的符号．

查看试题解析
24. 比较 $\frac{a^{2} + b^{2}}{2}$ 与（ $\frac{a + b}{2}$ ）²的大小．

查看试题解析
25. 已知a，b是正数，且a≠b，比较a³+b³与a²b+ab²的大小．

查看试题解析

人教新课标高中数学必修5 第三章不等式 3.1不等关系与不等式 同步测试

一、单选题

二、填空题

三、解答题

人教新课标高中数学必修5 第三章不等式 3.1不等关系与不等式同步测试