2016-2017学年甘肃省平凉十中九年级上学期期中数学试卷
试卷更新日期:2017-01-11 类型:期中考试
一、选择题
-
1. 下列关于x的方程中,是一元二次方程的是( )A、ax2+bx+c=0 B、x2+ =0 C、3x2+2xy=1 D、x2=62. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列命题中真命题是( )A、全等的两个图形是中心对称图形 B、中心对称图形都是轴对称图形 C、轴对称图形都是中心对称图形 D、关于中心对称的两个图形全等4. 将抛物线y=3x2向右平移两个单位,再向下平移4个单位,所得抛物线是( )A、y=3(x+2)2+4 B、y=3(x﹣2)2+4 C、y=3(x﹣2)2﹣4 D、y=3(x+2)2﹣45. 已知直角三角形的两边长是方程x2﹣7x+12=0的两根,则第三边长为( )A、7 B、5 C、 D、5或6. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论
3. 下列命题中真命题是( )A、全等的两个图形是中心对称图形 B、中心对称图形都是轴对称图形 C、轴对称图形都是中心对称图形 D、关于中心对称的两个图形全等4. 将抛物线y=3x2向右平移两个单位,再向下平移4个单位,所得抛物线是( )A、y=3(x+2)2+4 B、y=3(x﹣2)2+4 C、y=3(x﹣2)2﹣4 D、y=3(x+2)2﹣45. 已知直角三角形的两边长是方程x2﹣7x+12=0的两根,则第三边长为( )A、7 B、5 C、 D、5或6. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论①a>0,②b>0,③c>0,④b2﹣4ac>0
其中正确的有( )
 A、1个 B、2个 C、3个 D、4个7. 方程(2x+3)(x﹣1)=1的解的情况是( )A、有两个不相等的实数根 B、没有实数根 C、有两个相等的实数根 D、有一个实数根8. (﹣1,y1),(2,y2)与(3,y3)为二次函数y=﹣x2﹣4x+5图象上的三点,则y1 , y2 , y3的大小关系是( )A、y1<y2<y3 B、y3<y2<y1 C、y3<y1<y2 D、y2<y1<y39. 在同一直角坐标系中,一次函数y=ax+c和二次函数y=ax2+c的图象大致为( )A、
A、1个 B、2个 C、3个 D、4个7. 方程(2x+3)(x﹣1)=1的解的情况是( )A、有两个不相等的实数根 B、没有实数根 C、有两个相等的实数根 D、有一个实数根8. (﹣1,y1),(2,y2)与(3,y3)为二次函数y=﹣x2﹣4x+5图象上的三点,则y1 , y2 , y3的大小关系是( )A、y1<y2<y3 B、y3<y2<y1 C、y3<y1<y2 D、y2<y1<y39. 在同一直角坐标系中,一次函数y=ax+c和二次函数y=ax2+c的图象大致为( )A、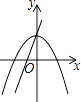 B、
B、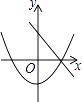 C、
C、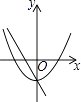 D、
D、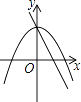 10. 如图,在四边形ABCD中,∠ADC=∠ABC=90°,AD=CD,DP⊥AB于P.若四边形ABCD的面积是18,则DP的长是( )
10. 如图,在四边形ABCD中,∠ADC=∠ABC=90°,AD=CD,DP⊥AB于P.若四边形ABCD的面积是18,则DP的长是( )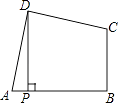 A、3 B、2 C、3 D、
A、3 B、2 C、3 D、二、填空题
-
11. 要使二次根式 有意义,字母x必须满足的条件是12. 已知点A(a,1)与点A′(5,b)是关于原点对称,则a= , b= .13. 若函数 是二次函数,则m的值为 .
14. 使分式 的值等于零的x的值是15. 已知y= (x+1)2﹣2,图象的顶点坐标为 , 当x时,函数值随x的增大而减小.16. 已知二次函数y=kx2﹣7x﹣7的图象和x轴有交点,则k的取值范围 .17. 如图,△COD是△AOB绕点O顺时针旋转40°后得到的图形,若点C恰好落在AB上,且∠AOD的度数为90°,则∠B的度数是 . 18. 二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如表
18. 二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如表x
﹣1
0
1
3
y
﹣1
3
5
3
下列结论:
①ac<0;
②当x>1时,y的值随x值的增大而减小.
③3是方程ax2+(b﹣1)x+c=0的一个根;
④当﹣1<x<3时,ax2+(b﹣1)x+c>0.
其中正确的结论是 .
三、解答题
-
19. 用恰当的方法解方程.(1)、﹣x2+4x﹣5=0;(2)、3x(2x+1)=4x+2.20. 如图,在建立了平面直角坐标系的正方形网格中,A(2,2),B(1,0),C(3,1)

①请在图中作出△ABC关于x轴对称的图形△A1B1C1
②请在图中作出△ABC关于原点对称的图形△A2B2C2 .
21. 已知二次函数的图象的顶点是(﹣1,2),且经过(1,﹣6),求这个二次函数的解析式.22. 向阳村2014年的人均收入为1200元,2016年的人均收入为1452元,求人均收入的年平均增长率.23. 如图,一个二次函数的图象经过点A、C、B三点,点A的坐标为(﹣1,0),点B的坐标为(3,0),点C在y轴的正半轴上,且AB=OC.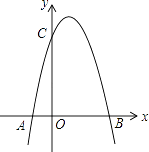 (1)、求点C的坐标;(2)、求这个二次函数的解析式,并求出该函数的最大值.24. 若α、β是方程x2﹣2x﹣3=0的两个实数根,求 的值.25. 已知关于x的一元二次方程(a+c)x2+2bx+(a﹣c)=0,其中a、b、c分别为△ABC三边的长.若方程有两个相等的实数根,试判断△ABC的形状,并说明理由.26. 如图,在Rt△OAB中,∠OAB=90°,OA=AB=6,将△OAB绕点O沿逆时针方向旋转90°得到△OA1B1 .
(1)、求点C的坐标;(2)、求这个二次函数的解析式,并求出该函数的最大值.24. 若α、β是方程x2﹣2x﹣3=0的两个实数根,求 的值.25. 已知关于x的一元二次方程(a+c)x2+2bx+(a﹣c)=0,其中a、b、c分别为△ABC三边的长.若方程有两个相等的实数根,试判断△ABC的形状,并说明理由.26. 如图,在Rt△OAB中,∠OAB=90°,OA=AB=6,将△OAB绕点O沿逆时针方向旋转90°得到△OA1B1 .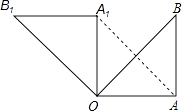 (1)、线段OA1的长是 , ∠AOB1的度数是;(2)、连接AA1 , 求证:四边形OAA1B1是平行四边形;(3)、求点B旋转到点B1的位置所经过的路线的长.27. 某商场销售一批名牌衬衫,平均每天可售出20件,每件赢利40元.为了扩大销售,商场决定采取适当的降价措施,经调查发现,如果每件衬衫降价1元,商场平均每天可多售出2件.(1)、若使商场平均每天赢利1200元,则每件衬衫应降价多少元?(2)、若想获得最大利润,每件衬衫应降价多少元?最大利润为多少元?28. 已知:二次函数y=x2+bx+c的图象与x轴交于A,B两点,其中A点坐标为(﹣3,0),与y轴交于点C,点D(﹣2,﹣3)在抛物线上.
(1)、线段OA1的长是 , ∠AOB1的度数是;(2)、连接AA1 , 求证:四边形OAA1B1是平行四边形;(3)、求点B旋转到点B1的位置所经过的路线的长.27. 某商场销售一批名牌衬衫,平均每天可售出20件,每件赢利40元.为了扩大销售,商场决定采取适当的降价措施,经调查发现,如果每件衬衫降价1元,商场平均每天可多售出2件.(1)、若使商场平均每天赢利1200元,则每件衬衫应降价多少元?(2)、若想获得最大利润,每件衬衫应降价多少元?最大利润为多少元?28. 已知:二次函数y=x2+bx+c的图象与x轴交于A,B两点,其中A点坐标为(﹣3,0),与y轴交于点C,点D(﹣2,﹣3)在抛物线上.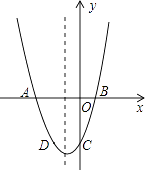 (1)、求抛物线的解析式;(2)、抛物线的对称轴上有一动点P,求出PA+PD的最小值;(3)、若抛物线上有一动点P,使三角形ABP的面积为6,求P点坐标.
(1)、求抛物线的解析式;(2)、抛物线的对称轴上有一动点P,求出PA+PD的最小值;(3)、若抛物线上有一动点P,使三角形ABP的面积为6,求P点坐标.