2016-2017学年山东省淄博市高青一中高一上学期期中数学试卷
试卷更新日期:2017-01-11 类型:期中考试
一、选择题
-
1. 已知集合U={1,3,5,7,9},A={1,5,7},则∁UA=( )A、{1,3} B、{3,7,9} C、{3,5,9} D、{3,9}2. 下列各组函数是同一函数的是( )A、y= ﹣2 B、y= C、 D、3. 函数y= ln(1﹣x)的定义域为( )A、(0,1) B、[0,1) C、(0,1] D、[0,1]4. 若函数f(x)= ,则f(2)的值为( )A、2 B、3 C、4 D、55. 函数f(x)=﹣x2+2(a﹣1)x+2在(﹣∞,4)上是增函数,则a的范围是( )A、a≥5 B、a≥3 C、a≤3 D、a≤﹣56. 若102x=25,则10﹣x等于( )A、 B、 C、 D、7. 如图所示,液体从一圆锥形漏斗漏入一圆柱形桶中,开始时,漏斗盛满液体,经过3分钟漏完.已知圆柱中液面上升的速度是一个常量,H是圆锥形漏斗中液面下落的距离,则H与下落时间t(分)的函数关系表示的图象只可能是( )
 A、
A、 B、
B、 C、
C、 D、
D、 8. 设函数f(x)和g(x)分别是R上的偶函数和奇函数,则下列结论恒成立的是( )A、f(x)+|g(x)|是偶函数 B、f(x)﹣|g(x)|是奇函数 C、|f(x)|+g(x)是偶函数 D、|f(x)|﹣g(x)是奇函数9. 若f(x)满足关系式f(x)+2( )=3x,则f(2)的值为( )A、1 B、﹣1 C、﹣ D、10. f(x)= 是定义在(﹣∞,+∞)上是减函数,则a的取值范围是( )A、[ , ) B、[0, ] C、(0, ) D、(﹣∞, ]11. f(x)满足对任意的实数a,b都有f(a+b)=f(a)•f(b),且f(1)=2,则 =( )A、1006 B、2016 C、2013 D、100812. 已知函数y=x2+2x在闭区间[a,b]上的值域为[﹣1,3],则满足题意的有序实数对(a,b)在坐标平面内所对应点组成图形为( )A、
8. 设函数f(x)和g(x)分别是R上的偶函数和奇函数,则下列结论恒成立的是( )A、f(x)+|g(x)|是偶函数 B、f(x)﹣|g(x)|是奇函数 C、|f(x)|+g(x)是偶函数 D、|f(x)|﹣g(x)是奇函数9. 若f(x)满足关系式f(x)+2( )=3x,则f(2)的值为( )A、1 B、﹣1 C、﹣ D、10. f(x)= 是定义在(﹣∞,+∞)上是减函数,则a的取值范围是( )A、[ , ) B、[0, ] C、(0, ) D、(﹣∞, ]11. f(x)满足对任意的实数a,b都有f(a+b)=f(a)•f(b),且f(1)=2,则 =( )A、1006 B、2016 C、2013 D、100812. 已知函数y=x2+2x在闭区间[a,b]上的值域为[﹣1,3],则满足题意的有序实数对(a,b)在坐标平面内所对应点组成图形为( )A、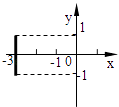 B、
B、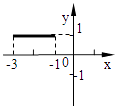 C、
C、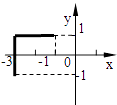 D、
D、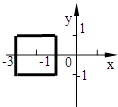
二、填空题
-
13. 已知集合M={0,x},N={1,2},若M∩N={1},则M∪N= .14. 若函数f(x)= 是奇函数,则a+b=15. 已知函数f(x)=x2+4mx+n在区间[2,6]上是减函数,求实数m的取值范围16. 如果函数f(x)= 是奇函数,则a= .
三、解答题
-
17. 已知函数 .
 (1)、在如图给定的直角坐标系内画出f(x)的图象;(直接画图,不需列表)(2)、写出f(x)的单调递增区间及值域.18. 已知f(x)是定义在R上的奇函数,且当x<0时, .(1)、求f(x)的表达式;(2)、判断并证明函数f(x)在区间(0,+∞)上的单调性.19. 已知函数f(x)的定义域为[﹣2,2],若对于任意的x,y∈[﹣2,2],都有f(x+y)=f(x)+f(y),且当x>0时,有f(x)>0(1)、证明:f(x)为奇函数;(2)、若f(1)=3求f(x)在[﹣2,2]上的值域.
(1)、在如图给定的直角坐标系内画出f(x)的图象;(直接画图,不需列表)(2)、写出f(x)的单调递增区间及值域.18. 已知f(x)是定义在R上的奇函数,且当x<0时, .(1)、求f(x)的表达式;(2)、判断并证明函数f(x)在区间(0,+∞)上的单调性.19. 已知函数f(x)的定义域为[﹣2,2],若对于任意的x,y∈[﹣2,2],都有f(x+y)=f(x)+f(y),且当x>0时,有f(x)>0(1)、证明:f(x)为奇函数;(2)、若f(1)=3求f(x)在[﹣2,2]上的值域.
20. 设定义域为R的函数 (a,b为实数).(1)、若f(x)是奇函数,求a,b的值;(2)、当f(x)是奇函数时,证明对任何实数x,c都有f(x)<c2﹣3c+3成立.21. 据气象中心观察和预测:发生于M地的沙尘暴一直向正南方向移动,其移动速度v(km/h)与时间t(h)的函数图象如图所示,过线段OC上一点T(t,0)作横轴的垂线l,梯形OABC在直线l左侧部分的面积即为t(h)内沙尘暴所经过的路程s(km). (1)、当t=4时,求s的值;(2)、将s随t变化的规律用数学关系式表示出来.22. 已知a>0且a≠1,函数f(x)=loga .(1)、求f(x)的定义域及其零点;(2)、设g(x)=mx2﹣2mx+3,当a>1时,若对任意x1∈(﹣∞,﹣1],存在x2∈[3,4],使得f(x1)≤g(x2),求实数m的取值范围.
(1)、当t=4时,求s的值;(2)、将s随t变化的规律用数学关系式表示出来.22. 已知a>0且a≠1,函数f(x)=loga .(1)、求f(x)的定义域及其零点;(2)、设g(x)=mx2﹣2mx+3,当a>1时,若对任意x1∈(﹣∞,﹣1],存在x2∈[3,4],使得f(x1)≤g(x2),求实数m的取值范围.