2016-2017学年北京七中七年级上学期期中数学试卷

试卷更新日期：2017-01-11 类型：期中考试

进入出卷网下载

一、选择题

1. 如果零上5℃记作+5℃，那么零下5℃记作（）

A、﹣5 B、﹣10 C、﹣10℃ D、﹣5℃

查看试题解析
2. 以下4个有理数中，最小的是（）

A、﹣1 B、1 C、﹣2 D、0

查看试题解析
3. 龙庆峡冰灯于2016年1月中旬接待游客．今年的龙庆峡冰灯以奥运五环、冬奥会运动项目等奥运元素为题材，分为彩灯区、娱乐区、冰展区，总面积达到200 000平方米．将200 000用科学记数法表示应为（）

A、20×10⁴ B、0.20×10⁶ C、2.0×10⁶ D、2.0×10⁵

查看试题解析
4. 如图，数轴上有A，B，C，D四个点，其中表示互为相反数的点是（）

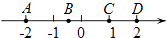A、点A与点B B、点B与点C C、点B与点D D、点A与点D

查看试题解析
5. 如果a是有理数，下列各式一定为正数的（）

A、a B、a+1 C、|a| D、a²+1

查看试题解析
6. 下列式子中，是单项式的是（）

A、﹣ $\frac{1}{2}$ x³yz² B、x+y C、﹣m²﹣n² D、 $\frac{1}{2 x}$

查看试题解析
7. 下列计算正确的是（　　）

A、3a+b=3ab B、3a﹣a=2 C、2a³+3a²=5a⁵ D、﹣a²b+2a²b=a²b

查看试题解析
8. ﹣（a﹣b+c）去括号的结果是（）

A、﹣a+b﹣c B、﹣a﹣b+c C、﹣a+b+c D、a+b﹣c

查看试题解析
9. 现有五种说法：①﹣a表示负数；②绝对值最小的有理数是0；③3×10²x²y是5次单项式；④ $\frac{x - y}{5}$ 是多项式．其中正确的是（）

A、①③ B、②④ C、②③ D、①④

查看试题解析
10. 若“！”是一种数学运算符号，并且1！=1，2！=2×1=2，3！=3×2×1=6，4！=4×3×2×1，…，则 $\frac{100!}{98!}$ 的值为（）

A、 $\frac{50}{49}$ B、99! C、9900 D、2！

查看试题解析

二、填空题

11. 根据要求，用四舍五入法取下列各数的近似数：1.4149≈（精确到千分位）

查看试题解析
12. 用代数式表示“a的3倍与b的差“是．

查看试题解析
13. 比较大小：﹣1﹣ $\frac{1}{3}$ ．

查看试题解析
14. 化简：﹣（﹣5）= ， ﹣|﹣5|= ．

查看试题解析
15. 若a^2mb³和﹣7a²b³是同类项，则m值为．

查看试题解析
16. 任意写一个含有字母a、b的三次二项式，常数项为﹣9，．

查看试题解析
17. 若|x﹣3|+（y﹣2）²=0，则y﹣x= ．

查看试题解析
18. 已知：（m﹣2）x﹣1=0是关于x的一元一次方程，则m ．

查看试题解析
19. 若a²+ab=5，ab+b²=4，则a²+2ab+b²的值为．

查看试题解析
20. 如图，数轴上，点A的初始位置表示的数为1，现点A做如下移动：第一次点A向左移动3个单位长度至点A₁ ，第2次从点A₁向右移动6个单位长度至点A₂ ，第3次从点A₂向左移动9个单位长度至点A₃ ， …，按照这种移动方式进行下去，点A₄表示的数是，如果点A_n与原点的距离不小于20，那么n的最小值是．

查看试题解析

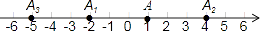
三、解答题

21. 计算

(1)、12﹣7+18﹣15

(2)、 $\frac{1}{4}$ ÷（﹣ $\frac{2}{3}$ ）×（﹣1 $\frac{3}{5}$ ）

(3)、（ $\frac{1}{4}$ ﹣ $\frac{1}{6}$ + $\frac{1}{12}$ ）×（﹣48）

(4)、﹣2⁴+（﹣5）²÷（﹣1 $\frac{1}{4}$ ）

查看试题解析
22. 化简

(1)、5x²+x+3+4x﹣8x²﹣2

(2)、（2x³﹣3x²﹣3）﹣（﹣x³+4x²）

(3)、3 （x²﹣5x+1）﹣2 （3x﹣6+x²）

查看试题解析
23. 先化简，再求值

(1)、4x﹣x²+2x³﹣（3x²+x+2x³），其中x=3．

(2)、4x²﹣xy﹣（ $\frac{4}{3}$ y²+2x²）+2（3xy﹣ $\frac{1}{3}$ y²），其中x=5，y= $\frac{1}{2}$ ．

查看试题解析
24. 解方程

(1)、﹣2x=4

(2)、x﹣10=7

(3)、x+13=5x+37

(4)、3x﹣x=﹣ $\frac{1}{2}$ +1．

查看试题解析
25. 有8筐白菜，以每筐25千克为标准，超过的千克数记作正数，不足的千克数记作负数，称后的记录如下：
回答下列问题：

(1)、这8筐白菜中，最接近25千克的那筐白菜为千克；

(2)、以每筐25千克为标准，这8筐白菜总计超过多少千克或不足多少千克？

(3)、若白菜每千克售价2.6元，则出售这8筐白菜可卖多少元？

查看试题解析
26. 某学校初一年级参加社会实践课，报名第一门课的有x人，第二门课的人数比第一门课的 $\frac{4}{5}$ 少20人，现在需要从报名第二门课的人中调出10人学习第一门课，那么：

(1)、报两门课的共有多少人？

(2)、调动后，报名第一门课的人数为人，第二门课人数为人．

(3)、调动后，报名第一门课比报名第二门课多多少人？计算出代数式后，请选择一个你觉得合适的x的值代入，并求出具体的人数．

查看试题解析

四、附加题

27. 下面的图表是我国数学家发明的“杨辉三角”，此图揭示了（a+b）ⁿ（n为非负整数）的展开式的项数及各项系数的有关规律．请你观察，并根据此规律写出：（a+b）⁷的展开式共有项，（a+b）ⁿ的展开式共有项，各项的系数和是．

查看试题解析
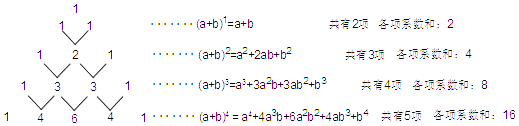28. 规定“*”表示一种运算，且a*b= $\frac{a - 2 b}{a b}$ ，则3*（4* $\frac{1}{2}$ ）的值是．

查看试题解析
29. 已知当x=2时，代数式ax³﹣bx+1的值为﹣17，求当x=﹣1时，代数式12ax﹣3bx³﹣5的值是多少？

查看试题解析
30. 已知|a+2|=﹣b² ，求： $\frac{2 a + 3 b}{2 a - 3 b} + 2002 b$ 的值？

查看试题解析
31. 阅读下面材料并解决有关问题：
我们知道：|x|= ${\begin{matrix} x (x > 0) \\ 0 (x = 0) \\ - x (x < 0) \end{matrix}$ ．现在我们可以用这一结论来化简含有绝对值的代数式，现在我们可以用这一结论来化简含有绝对值的代数式，如化简代数式|x+1|+|x﹣2|时，可令x+1=0和x﹣2=0，分别求得x=﹣1，x=2（称﹣1，2分别为|x+1|与|x﹣2|的零点值）．在实数范围内，零点值x=﹣1和，x=2可将全体实数分成不重复且不遗漏的如下3种情况：
①x＜﹣1；②﹣1≤x＜2；③x≥2．
从而化简代数式|x+1|+|x﹣2|可分以下3种情况：
①当x＜﹣1时，原式=﹣（x+1）﹣（x﹣2）=﹣2x+1；
②当﹣1≤x＜2时，原式=x+1﹣（x﹣2）=3；
③当x≥2时，原式=x+1+x﹣2=2x﹣1．综上讨论，原式= ${\begin{matrix} - 2 x + 1 (x < - 1) \\ 3 (- 1 \leq x < 2) \\ 2 x - 1 (x \geq 2) \end{matrix}$ ．
通过以上阅读，请你解决以下问题：

(1)、化简代数式|x+2|+|x﹣4|．

(2)、求|x﹣1|﹣4|x+1|的最大值．

查看试题解析