2016-2017学年广东省韶关市六校联考高三上学期期中数学试卷（文科）

试卷更新日期：2017-01-10 类型：期中考试

进入出卷网下载

一、选择题

1. 已知集合M={x| $\frac{x - 3}{x + 1}$ ≤0}，N={﹣3，﹣1，1，3，5}，则M∩N=（）

A、{1，3} B、{﹣1，1，3} C、{﹣3，1} D、{﹣3，﹣1，1}

查看试题解析
2. 已知复数z满足（5+12i）z=169，则 $\bar{z}$ =（）

A、﹣5﹣12i B、﹣5+12i C、5﹣12i D、5+12i

查看试题解析
3. “cosα=0”是“sinα=1”的（）

A、充分不必要条件 B、必要不充分条件 C、充分必要条件 D、既不充分也不必要条件

查看试题解析
4. 已知向量 $\vec{a}$ =（﹣1，0）， $\vec{b}$ =（ $\frac{\sqrt{3}}{2}$ ， $\frac{1}{2}$ ），则向量 $\vec{a}$ 与 $\vec{b}$ 的夹角为（）

A、 $\frac{π}{6}$ B、 $\frac{5 π}{6}$ C、 $\frac{π}{3}$ D、 $\frac{2 π}{3}$

查看试题解析
5. 设函数f（x）=﹣x²+4x﹣3，若从区间[2，6]上任取﹣个实数x₀ ，则所选取的实数x₀ ．满足f（x₀）≥0的概率为（）

A、 $\frac{1}{3}$ B、 $\frac{1}{4}$ C、 $\frac{3}{4}$ D、 $\frac{1}{2}$

查看试题解析
6. 椭圆C的焦点在x轴上，一个顶点是抛物线E：y²=16x的焦点，过焦点且垂直于长轴的弦长为2，则椭圆的离心率为（）

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{14}}{4}$ C、 $\frac{\sqrt{2}}{2}$ D、 $\frac{\sqrt{3}}{2}$

查看试题解析
7. 一个几何体的三视图如图所示，其中正视图和侧视图是腰长为2的两个全等的等腰直角三角形，俯视图是圆心角为 $\frac{π}{2}$ 的扇形，则该几何体的侧面积为（）

A、2 B、4+π C、4+ $\sqrt{2}$ π D、4+π+ $\sqrt{2}$ π

查看试题解析
8. 已知α∈（ $\frac{π}{2}$ ，π），且cosα=﹣ $\frac{5}{13}$ ，则 $\frac{\tan (α + \frac{π}{2})}{\cos (α + π)}$ =（）

A、 $\frac{12}{13}$ B、﹣ $\frac{12}{13}$ C、 $\frac{13}{12}$ D、﹣ $\frac{13}{12}$

查看试题解析
9. 已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜ $\frac{π}{2}$ ）的部分图象如图所示，若将f（x）图象上的所有点向右平移 $\frac{π}{6}$ 个单位得到函数g（x）的图象，则函数g（x）的单调递增区间为（）

A、[kπ﹣ $\frac{π}{4}$ ，kπ+ $\frac{π}{4}$ ]，k∈Z B、[2kπ﹣ $\frac{π}{4}$ ，2kπ+ $\frac{π}{4}$ ]，k∈Z C、[kπ﹣ $\frac{π}{3}$ ，kπ+ $\frac{π}{6}$ ]，k∈Z D、[2kπ﹣ $\frac{π}{3}$ ，2kπ+ $\frac{π}{6}$ ]，k∈Z

查看试题解析
10. 阅读如图所示的程序框图，若输入a的值为 $\frac{8}{17}$ ，则输出的k值是（）

A、9 B、10 C、11 D、12

查看试题解析
11. 已知函数f（x）= ${\begin{matrix} 2^{x - 2} - 1 ， x \geq 0 \\ x + 2 ， x < 0 \end{matrix}$ ，g（x）=x²﹣2x，则函数f[g（x）]的所有零点之和是（）

A、2 B、2 $\sqrt{3}$ C、1+ $\sqrt{3}$ D、0

查看试题解析
12. 对于三次函数f（x）=ax³+bx²+cx+d（a≠0），给出定义：设f′（x）是函数y=f（x）的导数，f″（x）是f′（x）的导数，若方程f″（x）=0有实数解x₀ ，则称点（x₀ ， f（x₀））为函数y=f（x）的“拐点”．经过探究发现：任何一个三次函数都有“拐点”；任何一个三次函数都有对称中心，且“拐点”就是对称中心．设函数g（x）=2x³﹣3x²+ $\frac{1}{2}$ ，则g（ $\frac{1}{100}$ ）+g（ $\frac{2}{100}$ ）+…+g（ $\frac{99}{100}$ ）=（）

A、100 B、50 C、 $\frac{99}{2}$ D、0

查看试题解析

二、填空题

13. 已知实数x，y满足 ${\begin{matrix} y \leq 2 x \\ 2 x - 5 y - 8 \leq 0 \\ y \leq 4 - x \end{matrix}$ ，则z=x+2y的最小值为．

查看试题解析
14. 已知函数f（x）=lnx﹣ax² ，且函数f（x）在点（2，f（2））处的切线的斜率是﹣ $\frac{1}{2}$ ，则a= ．

查看试题解析
15. 已知H是球O的直径AB上一点，AH：HB=1：3，AB⊥平面α，H为垂足，α截球O所得截面的面积为π，则球O的半径为．

查看试题解析
16. 已知△ABC满足BC•AC=2 $\sqrt{2}$ ，若C= $\frac{3 π}{4}$ ， $\frac{\sin A}{s i n B}$ = $\frac{1}{2 \cos (A + B)}$ ，则AB= ．

查看试题解析

三、解答题

17. 已知等差数列{a_n}的前n项和为S_n ，且S₃=9，a₁ ， a₃ ， a₇成等比数列．

(1)、求数列{a_n}的通项公式；

(2)、若a_n≠a₁时，数列{b_n}满足b_n=2 $^{a_{n}}$ ，求数列{b_n}的前n项和T_n ．

查看试题解析
18. 某商店计划每天购进某商品若干件，商店每销售1件该商品可获利50元．若供大于求，剩余商品全部退回，则每件商品亏损10元；若供不应求，则从外部调剂，此时每件调剂商品可获利30元．

(1)、若商店一天购进该商品10件，求当天的利润y（单位：元）关于当天需求量n（单位：件，n∈N）的函数解析式；

(2)、商店记录了50天该商品的日需求量（单位：件），整理得表：
日需求量n
8
9
10
11
12
频数
10
10
15
10
5
①假设该店在这50天内每天购进10件该商品，求这50天的日利润（单位：元）的平均数；
②若该店一天购进10件该商品，记“当天的利润在区间[400，550]”为事件A，求P（A）的估计值．

查看试题解析
19. 如图，ABC﹣A₁B₁C₁是底面边长为2，高为 $\frac{\sqrt{3}}{2}$ 的正三棱柱，经过AB的截面与上底面相交于PQ，设C₁P=λC₁A₁（0＜λ＜1）．、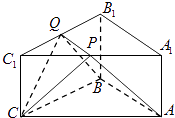

(1)、证明：PQ∥A₁B₁；

(2)、当 $λ = \frac{1}{2}$ 时，求点C到平面APQB的距离．

查看试题解析
20. 已知椭圆C的两个焦点分别为F₁（﹣ $\sqrt{10}$ ，0），F₂（ $\sqrt{10}$ ，0），且椭圆C过点P（3，2）．

(1)、求椭圆C的标准方程；

(2)、与直线OP平行的直线交椭圆C于A，B两点，求△PAB面积的最大值．

查看试题解析
21. 已知函数f（x）=2lnx﹣ax+a（a∈R）．

(1)、讨论f（x）的单调性；

(2)、若f（x）≤0恒成立，证明：当0＜x₁＜x₂时， $\frac{f (x_{2}) - f (x_{1})}{x_{2} - x_{1}} < 2 (\frac{1}{x_{1}} - 1)$ ．

查看试题解析
22. 如图，已知圆O是△ABC的外接圆，AB=BC，AD是 BC边上的高，AE 是圆O的直径，过点C作圆O的切线交BA的延长线于点F．

(1)、求证：AC•BC=AD•AE；

(2)、若AF=2，CF=2 $\sqrt{2}$ ，求AE的长．

查看试题解析
23. 在平面直角坐标系xOy中，直线l的参数方程为 ${\begin{matrix} x = 1 - \frac{1}{2} t \\ y = \frac{\sqrt{3}}{2} t \end{matrix}$ （ t为参数）．以原点为极点，x轴正半轴为极轴建立极坐标系，圆C的方程为 ρ=2 $\sqrt{3}$ sinθ．

(1)、写出直线l的普通方程和圆C的直角坐标方程；

(2)、若点P的直角坐标为（1，0），圆C与直线l交于A，B两点，求|PA|+|PB|的值．

查看试题解析
24. 已知函数f（x）=|x+a|+|x+ $\frac{1}{a}$ |（a＞0）

(1)、当a=2时，求不等式f（x）＞3的解集；

(2)、证明： $f (m) + f (- \frac{1}{m}) \geq 4$ ．

查看试题解析

日需求量n	8	9	10	11	12
频数	10	10	15	10	5