安徽省六安市霍邱县2018届数学中考一模试卷

试卷更新日期：2018-06-15 类型：中考模拟

进入出卷网下载

一、单选题

1. ﹣8的立方根是（）

A、﹣2 B、±2 C、2 D、﹣ $\frac{1}{2}$

查看试题解析
2. 某几何体的三视图如图，则该几何体是（）

A、三棱柱 B、长方体 C、圆柱 D、圆锥

查看试题解析
3. 已知点A（﹣2，y₁），B（﹣1，y₂）在反比例函数y=﹣ $\frac{6}{x}$ 上，则y₁与y₂的大小关系是（）

A、y₁＞y₂ B、y₁＜y₂ C、y₁≥y₂ D、无法比较

查看试题解析
4. 下列计算正确的是（）

A、a+2a²=3a³ B、（a³）²=a⁵ C、a³•a²=a⁶ D、a⁶÷a²=a⁴

查看试题解析
5. 小王参加某企业招聘测试，他的笔试、面试、技能操作得分分别为85分、80分、90分，若依次按照2：3：5的比例确定成绩，则小王的成绩是（）

A、255分 B、84分 C、84.5分 D、86分

查看试题解析
6. 甲、乙两人在操场上赛跑，他们赛跑的路程S（米）与时间t（分钟）之间的函数关系如图所示，则下列说法错误的是（）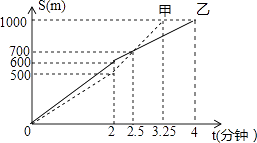

A、甲、乙两人进行1000米赛跑 B、甲先慢后快，乙先快后慢 C、比赛到2分钟时，甲、乙两人跑过的路程相等 D、甲先到达终点

查看试题解析
7. 九年级学生去距学校10 km的博物馆参观，一部分学生骑自行车先走，过了20 min后，其余学生乘汽车出发，结果他们同时到达.已知汽车的速度是骑车学生速度的2倍，求骑车学生的速度.设骑车学生的速度为x km/h，则所列方程正确的是（）

A、 $\frac{10}{x} = \frac{10}{2 x} - \frac{1}{3}$ B、 $\frac{10}{x} = \frac{10}{2 x} - 20$ C、 $\frac{10}{x} = \frac{10}{2 x} + \frac{1}{3}$ D、 $\frac{10}{x} = \frac{10}{2 x} + 20$

查看试题解析
8. 如图，在△ABC中，∠ABC=90°，AB=8，BC=6．若DE是△ABC的中位线，延长DE交△ABC的外角∠ACM的平分线于点F，则线段DF的长为（）

A、7 B、8 C、9 D、10

查看试题解析
9. 如图，已知正△ABC的边长为2，E，F，G分别是AB，BC，CA上的点，且AE=BF=CG，设△EFG的面积为y，AE的长为x，则y关于x的函数图象大致是（）

A、 B、 C、 D、

查看试题解析
10. 如图，半径为3的⊙O内有一点A，OA= $\sqrt{3}$ ，点P在⊙O上，当∠OPA最大时，PA的长等于（）

A、 $\sqrt{3}$ B、 $\sqrt{6}$ C、3 D、2 $\sqrt{3}$

查看试题解析

二、填空题

11. 2017年末，全国农村贫困人口3046万人，比上年末减少1289万人，其中3046万人用科学记数法表示为人．

查看试题解析
12. 因式分解：x﹣xy²= ．

查看试题解析
13. 某商厦10月份的营业额为50万元，第四季度的营业额为182万元，若设后两个月平均营业额的增长率为x，则由题意可得方程：．

查看试题解析
14. 如图，正方形ABCD的边长是16，点E在边AB上，AE=3，点F是边BC上不与点B，C重合的一个动点，把△EBF沿EF折叠，点B落在B′处．若△CDB′恰为等腰三角形，则DB′的长为．

查看试题解析

三、解答题

15. 计算： $\sqrt{9}$ +|﹣4|+（﹣1）⁰﹣（ $\frac{1}{2}$ ）^﹣¹ ．

查看试题解析
16. 如下数表是由1开始的连续自然数组成的，观察规律并完成各题的解答．

(1)、表示第9行的最后一个数是．

(2)、用含n的代数式表示：第n行的第一个数是，第n行共有个数；第n行各数之和是．

查看试题解析
17. 在正方形网格中建立如图所示的平面直角坐标系xOy，△ABC的三个顶点都在格点上，点A的坐标是（4，4），请解答下列问题：

(1)、①将△ABC向下平移5个单位长度，画出平移后的△A₁B₁C₁并写出点A的对应点A₁的坐标；②画出△A₁B₁C₁关于y轴对称的△A₂B₂C₂；

(2)、将△ABC绕点C逆时针旋转90°，画出旋转后的△A₃B₃C．

查看试题解析
18. 如图，某次中俄“海上联合”反潜演习中，我军舰A测得潜艇C的俯角为30°．位于军舰A正上方1000米的反潜直升机B侧得潜艇C的俯角为68°．试根据以上数据求出潜艇C离开海平面的下潜深度．（结果保留整数．参考数据：sin68°≈0.9，cos68°≈0.4，tan68°≈2.5， $\sqrt{3}$ ≈1.7）

查看试题解析
19. 如图，四边形OABC是平行四边形，以O为圆心，OA为半径的圆交AB于D，延长AO交O于E，连接CD，CE，若CE是⊙O的切线，解答下列问题：

(1)、求证：CD是⊙O的切线；

(2)、若BC=4，CD=6，求平行四边形OABC的面积．

查看试题解析
20. 春节期间，某商场计划购进甲、乙两种商品，已知购进甲商品2件和乙商品3件共需270元；购进甲商品3件和乙商品2件共需230元．

(1)、求甲、乙两种商品每件的进价分别是多少元？

(2)、商场决定甲商品以每件40元出售，乙商品以每件90元出售，为满足市场需求，需购进甲、乙两种商品共100件，且甲种商品的数量不少于乙种商品数量的4倍，请你求出获利最大的进货方案，并求出最大利润．

查看试题解析
21. 今年5月份，某校九年级学生参加了南宁市中考体育考试，为了了解该校九年级（1）班同学的中考体育情况，对全班学生的中考体育成绩进行了统计，并绘制以下不完整的频数分布表（如表）和扇形统计图（如图），根据图表中的信息解答下列问题：

(1)、求全班学生人数和m的值．

(2)、直接写出该班学生的中考体育成绩的中位数落在哪个分数段．

(3)、该班中考体育成绩满分共有3人，其中男生2人，女生1人，现需从这3人中随机选取2人到八年级进行经验交流，请用“列表法”或“画树状图法”求出恰好选到一男一女的概率．
分组
分数段（分）
频数
A
36≤x＜41
2
B
41≤x＜46
5
C
46≤x＜51
15
D
51≤x＜56
m
E
56≤x＜61
10

查看试题解析
22. 如图，有长为30m的篱笆，一面利用墙（墙的最大可用长度为10m），围成中间隔有一道篱笆（平行于AB）的矩形花圃．设花圃的一边AB为xm，面积为ym² ．

(1)、求y与x的函数关系式；

(2)、如果要围成面积为63m²的花圃，AB的长是多少？

(3)、能围成比63m²更大的花圃吗？如果能，请求出最大面积；如果不能，请说明理由．

查看试题解析
23. 如图

(1)、如图1，△ABC中，∠C=90°，AB的垂直平分线交AC于点D，连接BD．若AC=2，BC=1，则△BCD的周长为；

(2)、O为正方形ABCD的中心，E为CD边上一点，F为AD边上一点，且△EDF的周长等于AD的长．
①在图2中求作△EDF（要求：尺规作图，不写作法，保留作图痕迹）；
②在图3中补全图形，求∠EOF的度数；

查看试题解析

分组	分数段（分）	频数
A	36≤x＜41	2
B	41≤x＜46	5
C	46≤x＜51	15
D	51≤x＜56	m
E	56≤x＜61	10