安徽省蚌埠市禹会区2018届数学中考一模试卷
试卷更新日期：2018-06-15 类型：中考模拟
一、单选题
-
1. －4的相反数是 （ ）A、 B、－4 C、－ D、42. “宁安”高铁接通后，某市交通通行和转换能力成倍增长，极大地方便了广大市民出行，该工程投资预算930000万元，这一数据用科学记数法表示为 （ ）A、9.3×105 B、9.3×106 C、0.93×106 D、9.3×1043. 如图所示的几何体的俯视图是 （ ）
A、
B、
C、
D、
4. 下列运算中，正确的是（ ）A、4a﹣3a=1 B、a•a2=a3 C、3a6÷a3=3a2 D、（ab2）2=a2b25.如图，已知直线AB∥CD，∠BEG的平分线EF交CD于点F，若∠1=42°，则∠2等于（ ）
A、159° B、148° C、142° D、138°6. 我市某中学举办了一次以“我的中国梦”为主题的演讲比赛，最后确定7名同学参加决赛，他们的决赛成绩各不相同，其中李华已经知道自己的成绩，但能否进前四名，他还必须清楚这名同学成绩的（ ）A、众数 B、中位数 C、平均数 D、方差7. 下列二次函数中，图象以直线x=2为对称轴、且经过点（0，1）的是（ ）A、y=（x﹣2）2+1 B、y=（x+2）2+1 C、y=（x﹣2）2﹣3 D、y=（x+2）2﹣38. 某市2017年国内生产总值(GDP)比2016年增长了12％，预计今年(2018年)比2017年增长7％，若这两年年平均增长率为x％，则x％满足的关系是 （ ）A、12％＋7％＝x％ B、(1＋12％)(1＋7％)＝2(1＋x％) C、12％＋7％＝2x％ D、(1＋12％)(l＋7％)＝(1＋x％)29. 如图1，分别以直角三角形三边为边向外作等边三角形，面积分别为S1、S2、S3；如图2，分别以直角三角形三个顶点为圆心，三边长为半径向外作圆心角相等的扇形，面积分别为S4、S5、S6。其中，S1＝16，S2＝45，S5＝11，S6＝14，则S3＋S4＝（ ）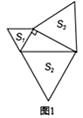
A、86 B、64 C、54 D、4810. 如图，在矩形ABCD中，AB＝3，AD＝4，以BC为斜边在矩形的外部作直角三角形BEC，点F是CD的中点，则EF的最大值为（ ）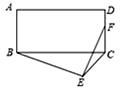
A、 B、4 C、5 D、二、填空题
-
11. 如图，若点A的坐标为（1， ），则sin∠1= ．
12. 分解因式：4ax2﹣ay2= ．13. 如图，一块等边三角形的木板，边长为1，现将木板沿水平线翻滚，那么B点从开始至结束所走过的路径长度为 ．
14. 如图1，将正方形纸片ABCD对折，使AB与CD重合，折痕为EF．如图2，展开后再折叠一次，使点C与点E重合，折痕为GH，点B的对应点为点M，EM交AB于N．若AD=2，则MN= ．
三、解答题
-
15. 计算：( －1)0＋(－1)2015＋( )－1－2sin60°16. 解方程：x2﹣5x+3=017. △ABC在平面直角坐标系xOy中的位置如图所示．
①作△ABC关于点C成中心对称的△A1B1C1 ．
②将△A1B1C1向右平移4个单位，作出平移后的△A2B2C2 ．
③在x轴上求作一点P，使PA1+PC2的值最小，并求出点P的坐标
18. 如图所示，把一张长方形卡片ABCD放在每格宽度为12mm的横格纸中，恰好四个顶点都在横格线上，已知∠α=36°，求长方形卡片的周长．（精确到1mm）（参考数据：sin36°≈0.60，cos36°≈0.80，tan36°≈0.75）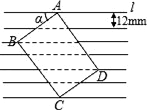
19. 如图，一次函数y=kx+b的图象与x轴交于点A，与反比例函数 （x＞0）的图象交于点B（2，n），过点B作BC⊥x轴于点C，点P（3n﹣4，1）是该反比例函数图象上的一点，且∠PBC=∠ABC，求反比例函数和一次函数的表达式．
20. 如图，已知△ABC为直角三角形，∠C=90°，边BC是⊙O的切线，切点为D，AB经过圆心O并与圆相交于点E，连接AD．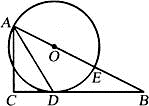
(1)、求证：AD平分∠BAC；(2)、若AC=8，tan∠DAC= ，求⊙O的半径．21. 2015年1月，市教育局在全市中小学中选取了63所学校从学生的思想品德、学业水平、学业负担、身心发展和兴趣特长五个维度进行了综合评价．评价小组在选取的某中学七年级全体学生中随机抽取了若干名学生进行问卷调查，了解他们每天在课外用于学习的时间，并绘制成如下不完整的统计图． 根据上述信息，解答下列问题：
(1)、本次抽取的学生人数是 ；扇形统计图中的圆心角α等于 ；补全统计直方图；(2)、被抽取的学生还要进行一次50米跑测试，每5人一组进行．在随机分组时，小红、小花两名女生被分到同一个小组，请用列表法或画树状图求出她俩在抽道次时抽在相邻两道的概率．22. 经统计分析，某市跨河大桥上的车流速度v（千米/小时）是车流密度x（辆/千米）的函数，当桥上的车流密度达到220辆/千米时，造成堵塞，此时车流速度为0千米/小时；当车流密度不超过20辆/千米时，车流速度为80千米/小时，研究表明：当20≤x≤220时，车流速度v是车流密度x的一次函数．(1)、求大桥上车流密度为100辆/千米时的车流速度；(2)、在交通高峰时段，为使大桥上的车流速度大于40千米/小时且小于60千米/小时，应控制大桥上的车流密度在什么范围内？(3)、车流量（辆/小时）是单位时间内通过桥上某观测点的车辆数，即：车流量=车流速度×车流密度．求大桥上车流量y的最大值．23. 如图（1），P为△ABC所在平面上一点，且∠APB=∠BPC=∠CPA=120°，则点P叫做△ABC的费马点．
(1)、如果点P为锐角△ABC的费马点，且∠ABC=60°．①求证：△ABP∽△BCP；
(2)、已知锐角△ABC，分别以AB、AC为边向外作正△ABE和正△ACD，CE和BD 相交于P点．如图（2）①求∠CPD的度数；
②求证：P点为△ABC的费马点．