安徽省蚌埠市固镇县2018届数学中考一模试卷

试卷更新日期：2018-06-15 类型：中考模拟

进入出卷网下载

一、单选题

1. ﹣2的绝对值是（）

A、2 B、﹣2 C、±2 D、 $\frac{1}{2}$

查看试题解析
2. 下列计算正确的是（）

A、 $（ a^{3} ）^{2} {=a}^{5}$ B、 $a^{6} \div a^{3} {=a}^{2}$ C、 $（ ab ）^{2} {=a}^{2} b^{2}$ D、 $（ a+b ）^{2} {=a}^{2} {+b}^{2}$

查看试题解析
3. 支付宝与“滴滴打车联合推出优惠，“滴滴打车”一夜之间红遍大江南北，据统计，2017年“滴滴打车账户流水总金额达到4930000000元，用科学记数法表示为（）

A、4.93×10⁸ B、4.93×10⁹ C、4.93×10¹⁰ D、4.93×10¹¹

查看试题解析
4. 如图，在一个长方体上放着一个小正方体，若这个组合体的俯视图如图所示，则这个组合体的左视图是（）

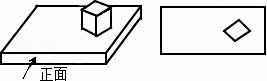A、 B、 C、 D、

查看试题解析
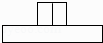
5. 不等式组 ${\begin{matrix} x - 1 \geq 0 \\ 1 - 0.5 x < 0 \end{matrix}$ 的最小整数解是（）

A、1 B、2 C、3 D、4

查看试题解析
6. 如图，已知直线AB∥CD，∠GEB的平分线EF交CD于点F，∠1=60°，则∠2等于（）

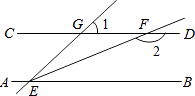A、130° B、140° C、150° D、160°

查看试题解析
7. 在某次体育测试中，九年级一班女同学的一分钟仰卧起坐成绩（单位:个）如下表：
成绩
45
46
47
48
49
50
人数
1
2
4
2
5
1
这此测试成绩的中位数和众数分别为（）

A、47, 49 B、48, 49 C、47.5, 49 D、48, 50

查看试题解析
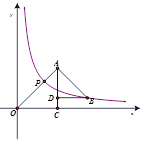
8.
如图所示，△OAC和△BAD都是等腰直角三角形，∠ACO=∠ADB=90°，反比例函数 $y= \frac{k}{x}$ 在第一象限的图像经过点B，与OA交于点P，若OA²-AB²=18，则点P的横坐标为（）

A、9 B、6 C、3 D、3 $\sqrt{2}$

查看试题解析
9. 如图，四边形ABCD是边长为1的正方形，E，F为BD所在直线上的两点．若AE= $\sqrt{5}$ ，∠EAF=135°，则以下结论正确的是（）

A、DE=1 B、tan∠AFO= $\frac{1}{3}$ C、AF= $\frac{\sqrt{10}}{2}$ D、四边形AFCE的面积为 $\frac{9}{4}$

查看试题解析
10. 二次函数y=ax²+bx+c（a≠0）的图象如图，下列四个结论：
①4a+c＜0；②m（am+b）+b＞a（m≠﹣1）；③关于x的一元二次方程ax²+（b﹣1）x+c=0没有实数根；④ak⁴+bk²＜a（k²+1）²+b（k²+1）（k为常数）．其中正确结论的个数是（）

A、4个 B、3个 C、2个 D、1个

查看试题解析

二、填空题

11. 分解因式：2xy²+4xy+2x= ．

查看试题解析
12. 已知实数x，y满足|x-4|+ $\sqrt{y - 8}$ =0，则以x，y的值为两边长的等腰三角形的周长是．

查看试题解析
13. 如图，在⊙O中，CD是直径，弦AB⊥CD，垂足为E，若∠C=22.5°，AB=6cm，则阴影部分面积为．

查看试题解析
14. 在▱ABCD中，AE平分∠BAD交边BC于E，DF平分∠ADC交边BC于F，若AD=11，EF=5，则AB= ．

查看试题解析

三、解答题

15. 计算：|﹣2|﹣（1+ $\sqrt{2}$ ）⁰+ $\sqrt{4}$ ﹣ $\frac{\sqrt{3}}{3}$ cos30°．

查看试题解析
16. 先化简下式，再求值：
2x²﹣[3（﹣ $\frac{1}{3}$ x²+ $\frac{2}{3}$ xy）﹣2y²]﹣2（x²﹣xy+2y²），其中x= $\frac{1}{2}$ ，y=﹣1．

查看试题解析
17. 已知：如图△ABC三个顶点的坐标分别为A（0，﹣3）、B（3，﹣2）、C（2，﹣4），正方形网格中，每个小正方形的边长是1个单位长度．
①画出△ABC向上平移6个单位得到的△A₁B₁C₁；
②以点C为位似中心，在网格中画出△A₂B₂C₂ ，使△A₂B₂C₂与△ABC位似，且△A₂B₂C₂与△ABC的位似比为2：1，并直接写出点A₂的坐标．

查看试题解析
18. 随着人们经济收入的不断提高，汽车已越来越多地进入到各个家庭．某大型超市为缓解停车难问题，建筑设计师提供了楼顶停车场的设计示意图．按规定，停车场坡道口上坡要张贴限高标志，以便告知车辆能否安全驶入．如图，地面所在的直线ME与楼顶所在的直线AC是平行的，CD的厚度为0.5m，求出汽车通过坡道口的限高DF的长（结果精确到0.1m，sin28°≈0.47，cos28°≈0.88，tan28°≈0.53）．

查看试题解析
19. 为了巩固全国文明城市建设成果，突出城市品质的提升，近年来，我市积极落实节能减排政策，推行绿色建筑，据统计，我市2014年的绿色建筑面积约为950万平方米，2016年达到了1862万平方米．若2015年、2016年的绿色建筑面积按相同的增长率逐年递增，请解答下列问题：

(1)、求这两年我市推行绿色建筑面积的年平均增长率；

(2)、2017年我市计划推行绿色建筑面积达到2400万平方米．如果2017年仍保持相同的年平均增长率，请你预测2017年我市能否完成计划目标？

查看试题解析
20. 中央电视台的“中国诗词大赛”节目文化品位高，内容丰富，某校初二年级模拟开展“中国诗词大赛”比赛，对全年级同学成绩进行统计后分为“优秀”、“良好”、“一般”、“较差”四个等级，并根据成绩绘制成如下两幅不完整的统计图，请结合统计图中的信息，回答下列问题：

(1)、扇形统计图中“优秀”所对应的扇形的圆心角为度，并将条形统计图补充完整．

(2)、此次比赛有四名同学活动满分，分别是甲、乙、丙、丁，现从这四名同学中挑选两名同学参加学校举行的“中国诗词大赛”比赛，请用列表法或画树状图法，求出选中的两名同学恰好是甲、丁的概率．

查看试题解析
21. 如图，AB是⊙O的直径，点C在⊙O上，∠ABC的平分线与AC相交于点D，与⊙O过点A的切线相交于点E．

(1)、∠ACB=°，理由是：；

(2)、猜想△EAD的形状，并证明你的猜想；

(3)、若AB=8，AD=6，求BD．

查看试题解析
22. 九年级某班数学兴趣小组经过市场调查整理出某种商品在第x天（1≤x≤90，且x为整数）的售价与销售量的相关信息如下．已知商品的进价为30元/件，设该商品的售价为y（单位：元/件），每天的销售量为p（单位：件），每天的销售利润为w（单位：元）．
时间x（天）
1
30
60
90
每天销售量p（件）
198
140
80
20

(1)、求出w与x的函数关系式；

(2)、问销售该商品第几天时，当天的销售利润最大？并求出最大利润；

(3)、该商品在销售过程中，共有多少天每天的销售利润不低于5600元？请直接写出结果．

查看试题解析
23. 如图1，在Rt△ABC中，∠C=90°，AC=6，BC=8，动点P从点A开始沿边AC向点C以1个单位长度的速度运动，动点Q从点C开始沿边CB向点B以每秒2个单位长度的速度运动，过点P作PD∥BC，交AB于点D，连接PQ分别从点A、C同时出发，当其中一点到达端点时，另一点也随之停止运动，设运动时间为t秒（t≥0）．

(1)、直接用含t的代数式分别表示：QB= ， PD= ．

(2)、是否存在t的值，使四边形PDBQ为菱形？若存在，求出t的值；若不存在，说明理由．并探究如何改变Q的速度（匀速运动），使四边形PDBQ在某一时刻为菱形，求点Q的速度；

(3)、如图2，在整个运动过程中，求出线段PQ中点M所经过的路径长．

查看试题解析

成绩	45	46	47	48	49	50
人数	1	2	4	2	5	1

时间x（天）	1	30	60	90
每天销售量p（件）	198	140	80	20