安徽省2018届初中毕业考试模拟冲刺数学卷(一)
试卷更新日期:2018-06-15 类型:中考模拟
一、单选题
-
1. 在实数2,0,-1,-2中,最小的实数是( )A、2 B、0 C、-1 D、-22. 下列二次根式中,与 的积为有理数的是( )A、 B、 C、 D、3. 近年来,随着交通网络的不断完善,我市近郊游持续升温.据统计,在今年“五一”期间,某风景区接待游览的人数约为20.3万人,这一数据用科学记数法表示为( )A、20.3×104人 B、2.03×105人 C、2.03×104人 D、2.03×103人4. 一个长方体和一个圆柱体按如图所示方式摆放,其主视图是( )
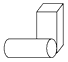 A、
A、 B、
B、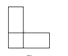 C、
C、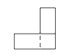 D、
D、 5. 设n= ,那么n值介于下列哪两数之间( )A、1与2 B、2与3 C、3与4 D、4与56. 某工厂今年1月份的产量是50万元,3月份的产值达到了72万元.若求2,3月份的产值平均增长率,设这两个月的产值平均月增长率为x,依题意可列方程( )A、72(x+1)2=50 B、50(x+1)2=72 C、50(x-1)2=72 D、72(x-1)2=507. 因干旱影响,市政府号召全市居民节约用水.为了了解居民节约用水的情况,小张在某小区随机调查了五户居民家庭2011年5月份的用水量:6吨,7吨,9吨,8吨,10吨.则关于这五户居民家庭月用水量的下列说法中,错误的是( )
5. 设n= ,那么n值介于下列哪两数之间( )A、1与2 B、2与3 C、3与4 D、4与56. 某工厂今年1月份的产量是50万元,3月份的产值达到了72万元.若求2,3月份的产值平均增长率,设这两个月的产值平均月增长率为x,依题意可列方程( )A、72(x+1)2=50 B、50(x+1)2=72 C、50(x-1)2=72 D、72(x-1)2=507. 因干旱影响,市政府号召全市居民节约用水.为了了解居民节约用水的情况,小张在某小区随机调查了五户居民家庭2011年5月份的用水量:6吨,7吨,9吨,8吨,10吨.则关于这五户居民家庭月用水量的下列说法中,错误的是( )
A、平均数是8吨 B、中位数是9吨 C、极差是4吨 D、方差是28. 如图所示,在折纸活动中,小明制作了一张△ABC纸片,点D,E分别在边AB,AC上,将△ABC沿着DE折叠压平,A与A′重合,若∠A=70°,则∠1+∠2=( )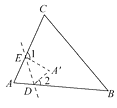 A、70° B、110° C、130° D、140°9. 如图所示,在矩形ABCD中,AB= ,BC=2,对角线AC,BD相交于点O,过点O作OE垂直AC交AD于点E,则AE的长是( )
A、70° B、110° C、130° D、140°9. 如图所示,在矩形ABCD中,AB= ,BC=2,对角线AC,BD相交于点O,过点O作OE垂直AC交AD于点E,则AE的长是( )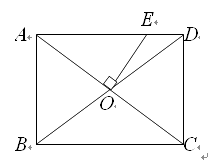 A、 B、 C、1 D、1.510. 正方形ABCD边长为1,E,F,G,H分别为边AB,BC,CD,DA上的点,且AE=BF=CG=DH.设小正方形EFGH的面积为y,AE=x. 则y关于x的函数图象大致是( )A、
A、 B、 C、1 D、1.510. 正方形ABCD边长为1,E,F,G,H分别为边AB,BC,CD,DA上的点,且AE=BF=CG=DH.设小正方形EFGH的面积为y,AE=x. 则y关于x的函数图象大致是( )A、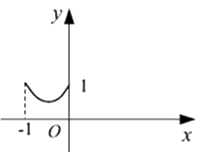 B、
B、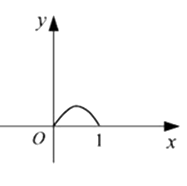 C、
C、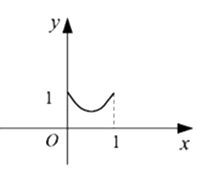 D、
D、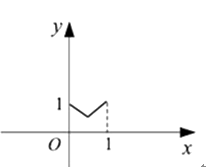
二、填空题
-
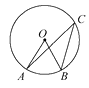
11. 计算: = .12. 如图,☉O的半径是2,∠ACB=30°,则弧AB的长是.(结果保留π)
 13. 按一定规律排列的一列数依次为 , , , , ,…,按此规律排列下去,这列数的第n个数是.(n是正整数)14. 如图,E,F,G,H分别是BD,BC,AC,AD的中点,且AB=CD.下列结论:①EG⊥FH,②四边形EFGH是矩形,③HF平分∠EHG,④EG= (BC-AD),⑤四边形EFGH是菱形.其中正确的是(把所有正确结论的序号都选上).
13. 按一定规律排列的一列数依次为 , , , , ,…,按此规律排列下去,这列数的第n个数是.(n是正整数)14. 如图,E,F,G,H分别是BD,BC,AC,AD的中点,且AB=CD.下列结论:①EG⊥FH,②四边形EFGH是矩形,③HF平分∠EHG,④EG= (BC-AD),⑤四边形EFGH是菱形.其中正确的是(把所有正确结论的序号都选上).
三、解答题
-
15. 先化简,再求值: ,其中16. 解不等式组: ,并把解集在数轴上表示出来.
 17. 如图,方格中,每个小正方形的边长都是单位1,△ABC在平面直角坐标系中的位置如图.
17. 如图,方格中,每个小正方形的边长都是单位1,△ABC在平面直角坐标系中的位置如图.
①画出△ABC关于y轴对称的△A1B1C1.
②画出△ABC绕点O按逆时针方向旋转90°后的△A2B2C2.
③判断△A1B1C1和△A2B2C2是不是成轴对称?如果是,请在图中作出它们的对称轴.
18. 如图,李军在A处测得风筝(C处)的仰角为30°,同时在A处正对着风筝方向距A处30m的B处,李明测得风筝的仰角为60°.求风筝此时的高度.(结果保留根号) 19. 某校组织学生参观航天展览,甲、乙、丙、丁四位同学随机分成两组乘车.(1)、哪两位同学会被分到第一组,写出所有可能.(2)、用列表法(或树状图法)求甲、乙分在同一组的概率.
19. 某校组织学生参观航天展览,甲、乙、丙、丁四位同学随机分成两组乘车.(1)、哪两位同学会被分到第一组,写出所有可能.(2)、用列表法(或树状图法)求甲、乙分在同一组的概率.
20. 如图1,AB是☉O的直径,C为☉O上一点,直线CD与☉O相切于点C,AD⊥CD,垂足为D.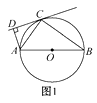
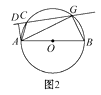 (1)、求证:△ACD∽△ABC.
(1)、求证:△ACD∽△ABC.
(2)、如图2,将直线CD向下平移与☉O相交于点C,G,但其他条件不变.若AG=4,BG=3,求tan∠CAD的值.
21. 如图,一次函数 与反比例函数 的图象交于A(2,3),B(-3,n)两点.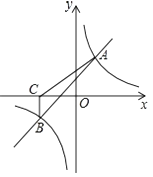 (1)、求一次函数与反比例函数的表达式;
(1)、求一次函数与反比例函数的表达式;
(2)、根据所给条件,请直接写出不等式 < 的解集;(3)、过点B作BC⊥x轴,垂足为C,求S△ABC .22. 星光中学课外活动小组准备围建一个矩形生物苗圃园,其中一边靠墙,另外三边用长为30米的篱笆围成.已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边的长为x米. (1)、若平行于墙的一边长为y米,直接写出y与x的函数关系式及其自变量x的取值范围;(2)、垂直于墙的一边的长为多少米时,这个苗圃园的面积最大,并求出这个最大值;(3)、当这个苗圃园的面积不小于88平方米时,试结合函数图象,直接写出x的取值范围.23. 如图1所示,在正方形ABCD和正方形CGEF中,点B、C、G在同一条直线上,M是线段AE的中点,DM的延长线交EF于点N,连接FM,易证:DM=FM,DM⊥FM(无需写证明过程)
(1)、若平行于墙的一边长为y米,直接写出y与x的函数关系式及其自变量x的取值范围;(2)、垂直于墙的一边的长为多少米时,这个苗圃园的面积最大,并求出这个最大值;(3)、当这个苗圃园的面积不小于88平方米时,试结合函数图象,直接写出x的取值范围.23. 如图1所示,在正方形ABCD和正方形CGEF中,点B、C、G在同一条直线上,M是线段AE的中点,DM的延长线交EF于点N,连接FM,易证:DM=FM,DM⊥FM(无需写证明过程)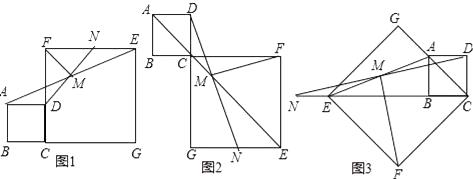 (1)、如图2,当点B、C、F在同一条直线上,DM的延长线交EG于点N,其余条件不变,试探究线段DM与FM有怎样的关系?请写出猜想,并给予证明;
(1)、如图2,当点B、C、F在同一条直线上,DM的延长线交EG于点N,其余条件不变,试探究线段DM与FM有怎样的关系?请写出猜想,并给予证明;
(2)、如图3,当点E、B、C在同一条直线上,DM的延长线交CE的延长线于点N,其余条件不变,探究线段DM与FM有怎样的关系?请直接写出猜想.