安徽省2018届初中毕业考试模拟冲刺数学卷(四)
试卷更新日期:2018-06-15 类型:中考模拟
一、单选题
-
1. 如果a与2互为相反数,则下列结论正确的为( )A、a= B、a=-2 C、a= D、a=22. 小杰从正面(图示“主视方向”)观察左边的热水瓶时,得到的俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 计算(-2a2)·3a的结果是( )A、-6a2 B、-6a3 C、12a3 D、6a34. 下列各式能用完全平方公式进行分解因式的是( )
3. 计算(-2a2)·3a的结果是( )A、-6a2 B、-6a3 C、12a3 D、6a34. 下列各式能用完全平方公式进行分解因式的是( )
A、x2+1 B、x2+2x-1 C、x2+x+1 D、x2+4x+45. 某商品原价为180元,连续两次提价x%后售价为300元,下列所列方程正确的是( )A、180(1+x%)=300 B、180(1+x%)2=300 C、180(1-x%)=300 D、180(1-x%)2=3006. 计算 的结果是( )A、﹣ B、 C、 D、7. 如图,点O是正六边形的对称中心,如果用一副三角板的角,借助点O(使该角的顶点落在点O处),把这个正六边形的面积n等分,那么n的所有可能取值的个数是( )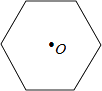 A、4 B、5 C、6 D、78. 经过某十字路口的汽车,它可能继续直行,也可能向左或向右转.若这三种可能性大小相同,则两辆汽车经过该十字路口全部继续直行的概率为( )A、 B、 C、 D、9.
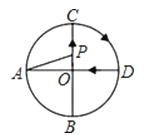
A、4 B、5 C、6 D、78. 经过某十字路口的汽车,它可能继续直行,也可能向左或向右转.若这三种可能性大小相同,则两辆汽车经过该十字路口全部继续直行的概率为( )A、 B、 C、 D、9.如图,AD、BC是⊙O的两条互相垂直的直径,点P从点O出发,沿O→C→D→O的路线匀速运动.设∠APB=y(单位:度),那么y与点P运动的时间x(单位:秒)的关系图是( )
 A、
A、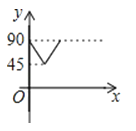 B、
B、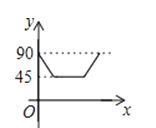 C、
C、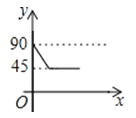 D、
D、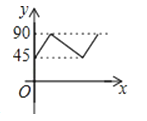 10. 如图,正方形A1A2A3A4 , A5A6A7A8 , A9A10A11A12 , …(每个正方形从第三象限的顶点开始,按顺时针方向顺序,依次记为A1 , A2 , A3 , A4;A5 , A6 , A7 , A8;A9 , A10 , A11 , A12;…)的中心均在坐标原点O,各边均与x轴或y轴平行,若它们的边长依次是2,4,6,…,则顶点A20的坐标为 ( )
10. 如图,正方形A1A2A3A4 , A5A6A7A8 , A9A10A11A12 , …(每个正方形从第三象限的顶点开始,按顺时针方向顺序,依次记为A1 , A2 , A3 , A4;A5 , A6 , A7 , A8;A9 , A10 , A11 , A12;…)的中心均在坐标原点O,各边均与x轴或y轴平行,若它们的边长依次是2,4,6,…,则顶点A20的坐标为 ( )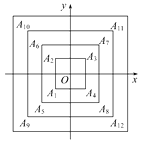 A、(5,5) B、(5,-5) C、(-5,5) D、(-5,-5)
A、(5,5) B、(5,-5) C、(-5,5) D、(-5,-5)二、填空题
-
11. 若﹣2xm﹣ny2与3x4y2m+n是同类项,则m﹣3n的立方根是 .12. 甲、乙、丙三位选手各10次射击成绩的平均数和方差,统计如下表:
选手
甲
乙
丙
平均数
9.3
9.3
9.3
方差
0.026
0.015
0.032
则射击成绩最稳定的选手是 . (填“甲”、“乙”、“丙”中的一个)
13. 如图,已知☉O是△ABC的外接圆,且∠C =70°,则∠OAB =.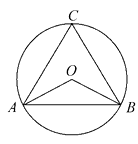 14. 如图,已知正方形ABCD的对角线交于O点,点E,F分别是AO,CO的中点,连接BE,BF,DE,DF,则下列结论中一定成立的是.(把所有正确结论的序号都填在横线上)①BF=DE;②∠ABO=2∠ABE;③S△AED= S△ACD;④四边形BFDE是菱形.
14. 如图,已知正方形ABCD的对角线交于O点,点E,F分别是AO,CO的中点,连接BE,BF,DE,DF,则下列结论中一定成立的是.(把所有正确结论的序号都填在横线上)①BF=DE;②∠ABO=2∠ABE;③S△AED= S△ACD;④四边形BFDE是菱形.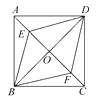
三、解答题
-
15. 计算:(m-n)(m+n)+(m+n)2-2m2.16. 解方程:x2-4x-1=0.17. 探索n×n的正方形钉子板上(n是钉子板每边上的钉子数,每边上相邻钉子间的距离为1),连接任意两个钉子所得到的不同长度值的线段种数:
当n=2时,钉子板上所连不同线段的长度值只有1与 ,所以不同长度值的线段只有2种,若用S表示不同长度值的线段种数,则S=2;
当n=3时,钉子板上所连不同线段的长度值只有1, ,2, ,2 五种,比n=2时增加了3种,即S=2+3=5.
(1)、观察图形,填写下表:钉子数(n×n)
S值
2×2
2
3×3
2+3
4×4
2+3+()
5×5
()
(2)、写出(n-1)×(n-1)和n×n的两个钉子板上,不同长度值的线段种数之间的关系;(用式子或语言表述均可).(3)、对n×n的钉子板,写出用n表示S的代数式.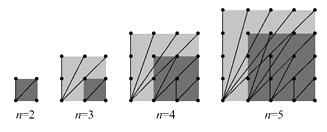 18. △ABC在平面直角坐标系中的位置如图所示,其中每个小正方形的边长为1个单位长度.
18. △ABC在平面直角坐标系中的位置如图所示,其中每个小正方形的边长为1个单位长度.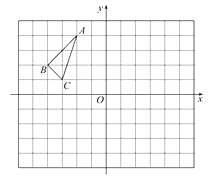
①将△ABC向右平移2个单位长度,作出平移后的△A1B1C1 , 并写出△A1B1C1各顶点的坐标.
②若将△ABC绕点(-1,0)顺时针旋转180°后得到△A2B2C2 , 并写出△A2B2C2各顶点的坐标.
③观察△A1B1C1和△A2B2C2 , 它们是否关于某点成中心对称?若是,请写出对称中心的坐标;若不是,说明理由.
19. 如图,在△ABC中,AD是BC上的高,tanB=cos∠DAC. (1)、求证:AC=BD(2)、若sin∠C= ,BC=12,求AD的长.20. 光明中学组织全校1000名学生进行了校园安全知识竞赛.为了解本次知识竞赛的成绩分布情况,从中随机抽取了部分学生的成绩(得分取正整数,满分为100分),并绘制了如图的频数分布表和频数分布直方图(不完整).
(1)、求证:AC=BD(2)、若sin∠C= ,BC=12,求AD的长.20. 光明中学组织全校1000名学生进行了校园安全知识竞赛.为了解本次知识竞赛的成绩分布情况,从中随机抽取了部分学生的成绩(得分取正整数,满分为100分),并绘制了如图的频数分布表和频数分布直方图(不完整).分组
频数
频率
50.5~60.5
10
a
60.5~70.5
b
70.5~80.5
0.2
80.5~90.5
52
0.26
90.5~100.5
0.37
合计
c
1
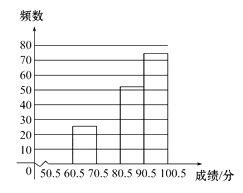
请根据以上提供的信息,解答下列问题:
(1)、直接写出频数分布表中a,b,c的值,补全频数分布直方图.(2)、上述学生成绩的中位数落在哪一组范围内?(3)、学校将对成绩在90.5~100.5分之间的学生进行奖励,请估计全校1000名学生中约有多少名获奖?21. 某商店5月1日举行促销优惠活动,当天到该商店购买商品有两种方案,方案一:用168元购买会员卡成为会员后,凭会员卡购买商店内任何商品,一律按商品价格的8折优惠;方案二:若不购买会员卡,则购买商店内任何商品,一律按商品价格的9.5折优惠.已知王老师5月1日前不是该商店的会员.(1)、若王老师不购买会员卡,所购买商品的价格为120元时,实际应支付多少元?(2)、请帮王老师算一算,所购买商品的价格在什么范围内时,采用方案一更合算?22. 如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于点A( , ),B(4,m),点P是线段AB上异于A,B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.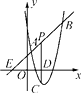 (1)、求抛物线的解析式;(2)、是否存在这样的P点,使线段PC的长有最大值?若存在,求出这个最大值;若不存在,请说明理由.23. 如图①,在四边形ABCD的边AB上任取一点E(点E不与A,B重合),分别连接ED,EC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把E叫做四边形ABCD的边AB上的“相似点”;如果这三个三角形都相似,我们就把E叫做四边形ABCD的边AB上的“强相似点”.
(1)、求抛物线的解析式;(2)、是否存在这样的P点,使线段PC的长有最大值?若存在,求出这个最大值;若不存在,请说明理由.23. 如图①,在四边形ABCD的边AB上任取一点E(点E不与A,B重合),分别连接ED,EC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把E叫做四边形ABCD的边AB上的“相似点”;如果这三个三角形都相似,我们就把E叫做四边形ABCD的边AB上的“强相似点”.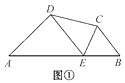 (1)、【试题再现】如图②,在△ABC中,∠ACB=90°,直角顶点C在直线DE上,分别过点A,B作AD⊥DE于点D,BE⊥DE于点E.求证:△ADC∽△CEB.
(1)、【试题再现】如图②,在△ABC中,∠ACB=90°,直角顶点C在直线DE上,分别过点A,B作AD⊥DE于点D,BE⊥DE于点E.求证:△ADC∽△CEB.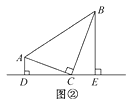 (2)、【问题探究】在图①中,若∠A=∠B=∠DEC=40°,试判断点E是否是四边形ABCD的边AB上的相似点,并说明理由.(3)、【深入探究】如图③,AD∥BC,DP平分∠ADC,CP平分∠BCD交DP于点P,过点P作AB⊥AD于点A,交BC于点B.
(2)、【问题探究】在图①中,若∠A=∠B=∠DEC=40°,试判断点E是否是四边形ABCD的边AB上的相似点,并说明理由.(3)、【深入探究】如图③,AD∥BC,DP平分∠ADC,CP平分∠BCD交DP于点P,过点P作AB⊥AD于点A,交BC于点B.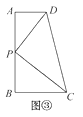
①请证明点P是四边形ABCD的边AB上的一个强相似点.
②若AD=3,BC=5,试求AB的长.