2016-2017学年湖北省黄冈市罗田县八年级上学期期中数学试卷
试卷更新日期：2017-01-10 类型：期中考试
一、精心选择
-
1. 在下列各电视台的台标图案中，是轴对称图形的是（ ）A、
B、
C、
D、
2. 下列说法正确的是（ ）A、三角形三条高的交点都在三角形内 B、三角形的角平分线是射线 C、三角形三边的垂直平分线不一定交于一点 D、三角形三条中线的交点在三角形内3. 已知点A（x，4）与点B（3，y）关于y轴对称，那么x+y的值是（ ）A、﹣1 B、﹣7 C、7 D、14. 正多边形的每个内角都等于135°，则该多边形是（ ）A、正八边形 B、正九边形 C、正十边形 D、正十一边形5.在正方形网格中，∠AOB的位置如图所示，到∠AOB两边距离相等的点应是（ ）
A、M点 B、N点 C、P点 D、Q点6. 如图，已知AB=AD，那么添加下列一个条件后，仍无法判定△ABC≌△ADC的是（ ）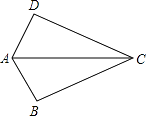
A、CB=CD B、∠BAC=∠DAC C、∠BCA=∠DCA D、∠B=∠D=90°7. 如图，在△ABC中，AD为∠BAC的平分线，DE⊥AB于E，DF⊥AC于F，△ABC的面积是28cm2 ， AB=20cm，AC=8cm，则DE的长是（ ）
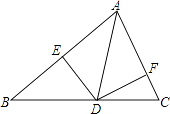A、4cm B、3cm C、2cm D、1cm8. 如图，在四边形ABCD中，AD∥BC，∠C=90°，BC=CD=8，过点B作EB⊥AB，交CD于点E．若DE=6，则AD的长为（ ）
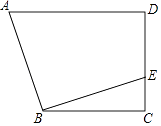A、6 B、8 C、9 D、10二、细心填空
-
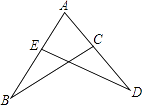
9. 如图，已知△ABC≌△ADE，若AB=7，AC=3，则BE的值为 ．
10. 一个等腰三角形的边长分别是4cm和7cm，则它的周长是11. 如图，在△ABC中，AB=AC，AB的垂直平分线交AC于D，交AB于E，若△ABC的周长为22，BC=6，则△BCD的周长为 ．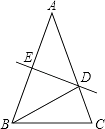
12. 如图，把一张长方形纸片ABCD沿EF折叠后，点A、B分别落在A1、B2的位置上，A1E与BC交于点O，若∠EFO=60°，则∠AEA1= ．
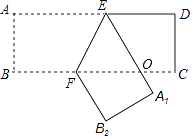13. 在△ABC中，∠B、∠C的平分线相交于点O，∠BOC=115°，则∠A的度数是 ．14. 已知直线l经过点（0，2），且与x轴平行，那么点（6，5）关于直线l的对称点为15. 如图，在△ABC中，AD是它的角平分线，AB：AC=8：5，则CD：BD= ．
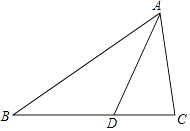16. 如图，在直角平面坐标系中，AB=BC，∠ABC=90°，A（3，0），B（0，﹣1），以AB为直角边在AB边的上方作等腰直角△ABE，则点E的坐标是 ．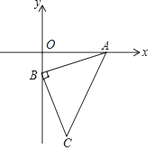
三、用心解答
-
17.
电信部门要修建一个电视信号发射塔．如图所示，按照要求，发射塔到两个城镇A，B的距离必须相等，到两条高速公路m和n的距离也必须相等．发射塔应修建在什么位置？在图上标出它的位置．
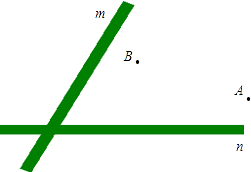18. 已知AB=AD，BC=DC．求证：AC平分∠BAD．
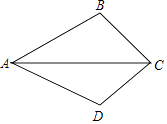19. 已知：在△ABC中，AD⊥BC，BE平分∠ABC交AD于F，∠ABE=23°．求∠AFE的度数．
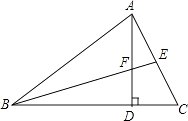20. 如图，三角形纸片中，AB=8cm，BC=6cm，AC=5cm．沿过点B的直线折叠这个三角形，使点C落在AB边上的点E处，折痕为BD，求△ADE的周长．
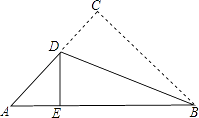21. 如图，已知∠A=90゜，AB=BD，ED⊥BC于D，求证：DE+CE=AC．
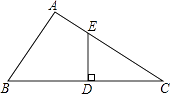22. 如图，在△ABC和△ADE中，AC=AB，AE=AD，∠CAB=∠EAD=90°
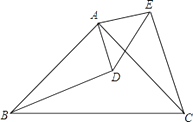(1)、求证：CE=BD；(2)、求证：CE⊥BD．四、灵活应用
-
23. 已知点P为∠EAF平分线上一点，PB⊥AE于B，PC⊥AF于C，点M，N分别是射线AE，AF上的点，且PM=PN．
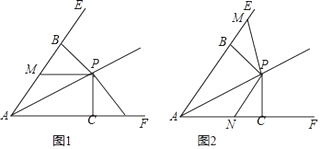(1)、如图1，当点M在线段AB上，点N在线段AC的延长线上时，求证：BM=CN；(2)、在（1）的条件下，直接写出线段AM，AN与AC之间的数量关系；(3)、如图2，当点M在线段AB的延长线上，点N在线段AC上时，若AC：PC=2：1，且PC=4，求四边形ANPM的面积．24. 如图，点B（0，b），点A（a，0）分别在y轴、x轴正半轴上，且满足 +（b2﹣16）2=0．
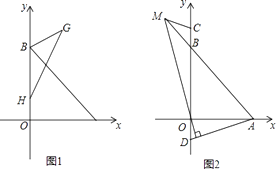(1)、求A、B两点的坐标，∠OAB的度数；(2)、如图1，已知H（0，1），在第一象限内存在点G，HG交AB于E，使BE为△BHG的中线，且S△BHE=3，①求点E到BH的距离；
②求点G的坐标；
(3)、如图2，C，D是y轴上两点，且BC=OD，连接AD，过点O作MN⊥AD于点N，交直线AB于点M，连接CM，求∠ADO+∠BCM的值．