2018年高考数学真题分类汇编专题05：平面向量（基础题）

试卷更新日期：2018-06-15 类型：二轮复习

进入出卷网下载

一、平面向量

1. 在 $Δ A B C$ 中，AD为BC边上的中线，E为AD的中点，则 $\vec{E B} =$ （）

A、 $\frac{3}{4} \vec{A B} - \frac{1}{4} \vec{A C}$ B、 $\frac{1}{4} \vec{A B} - \frac{3}{4} \vec{A C}$ C、 $\frac{3}{4} \vec{A B} + \frac{1}{4} \vec{A C}$ D、 $\frac{1}{4} \vec{A B} + \frac{3}{4} \vec{A C}$

查看试题解析
2. 已知向量 $\vec{a}$ ， $\vec{b}$ 满足 $|\vec{a}|$ =1， $\vec{a}$ ⋅ $\vec{b}$ =−1 ，则 $\vec{a}$ ·(2 $\vec{a}$ - $\vec{b}$ )=（）

A、4 B、3 C、2 D、0

查看试题解析
3. 设a ， b均为单位向量，则“ $| a - 3 b | = | 3 a + b |$ ”是“a $⊥ b$ ”的（）

A、充分而不必要条件 B、必要而不充分条件 C、充分必要条件 D、既不充分也不必要条件

查看试题解析
4. 如图，在平面四边形ABCD中， $A B ⊥ B C$ ， $A D ⊥ C D$ ， $∠ B A D = 120 °$ ， $A B = A D = 1$ . 若点E为边CD上的动点，则 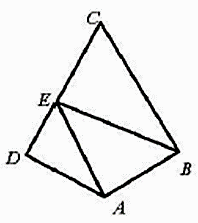$\vec{A E} \cdot \vec{B E}$ 的最小值为（）

A、 $\frac{21}{16}$ B、 $\frac{3}{2}$ C、 $\frac{25}{16}$ D、 $3$

查看试题解析
5. 在如图的平面图形中，已知 $O M = 1. O N = 2 ， ∠ M O N = 120^{\circ}$ ， $\vec{B M} = 2 \vec{M A} ， \vec{C N} = 2 \vec{N A} ，$ 则 $\vec{B C} · \vec{O M}$ 的值为（）

A、 $- 15$ B、 $- 9$ C、 $- 6$ D、0

查看试题解析
6. 已知a ， b ， e是平面向量，e是单位向量．若非零向量a与e的夹角为 $\frac{π}{3}$ ，向量b满足b²−4e·b+3=0，则|a−b|的最小值是（）

A、 $\sqrt{3}$ −1 B、 $\sqrt{3}$ +1 C、2 D、2− $\sqrt{3}$

查看试题解析
7. 在平面直角坐标系中，已知点A（-1，0），B（2，0），E，F是y轴上的两个动点，且| $\vec{EF}$ |=2，则 $\vec{AE}$ · $\vec{BF}$ 的最小值为

查看试题解析
8. 设向量a=（1，0），b=（-1，m），若a⊥（ma-b），则m=.

查看试题解析
9. 已知点 $M (- 1 ， 1)$ 和抛物线 $C ： y^{2} = 4 x$ ，过 $C$ 的焦点且斜率为 $k$ 的直线与 $C$ 交于 $A$ ， $B$ 两点．若 $∠ A M B = 90 °$ ，则 $k =$ ．

查看试题解析
10. 已知 $\vec{a} = (1 ， 2)$ ， $\vec{b} = (2 ， - 2)$ ， $\vec{c} = (1 ， λ)$ ，若 $\vec{c} ∥ (2 \vec{a} + \vec{b})$ ，则 $λ =$ 。

查看试题解析
11. 在平面直角坐标系 $X O Y$ 中， $A$ 为直线 $l ： y = 2 x$ 上在第一象限内的点， $B (5 ， 0)$ 以 $A B$ 为直径的圆 $C$ 与直线 $l$ 交于另一点 $D$ ，若 $\vec{A B} \cdot \vec{C D} = 0$ ，则点 $A$ 的横坐标为

查看试题解析