内蒙古鄂伦春自治旗2018届高三下学期理数二模试卷
试卷更新日期:2018-06-14 类型:高考模拟
一、单选题
-
1. 下列复数中虚部最大的是( )A、 B、 C、 D、2. 已知集合 , ,则 ( )A、 B、 C、 D、3. 若角 的终边经过点 ,则 ( )A、 B、 C、 D、4. 若双曲线 的一个焦点为 ,则 ( )A、 B、 C、 D、5. 在 中, , ,且 ,则 ( )A、 B、 C、 D、6. 甲、乙两个几何体的三视图如图所示(单位相同),记甲、乙两个几何体的体积分别为 , ,则( )
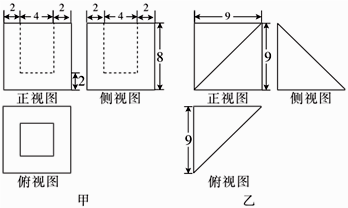 A、 B、 C、 D、7. 的展开式中 的系数为( )A、 B、84 C、 D、2808. 我国古代数学名著《九章算术》里有一道关于玉石的问题:“今有玉方一寸,重七两;石方一寸,重六两.今有石方三寸,中有玉,并重十一斤( 两).问玉、石重各几何?”如图所示的程序框图反映了对此题的一个求解算法,运行该程序框图,则输出的 , 分别为( )
A、 B、 C、 D、7. 的展开式中 的系数为( )A、 B、84 C、 D、2808. 我国古代数学名著《九章算术》里有一道关于玉石的问题:“今有玉方一寸,重七两;石方一寸,重六两.今有石方三寸,中有玉,并重十一斤( 两).问玉、石重各几何?”如图所示的程序框图反映了对此题的一个求解算法,运行该程序框图,则输出的 , 分别为( )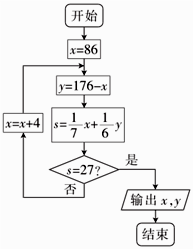 A、90,86 B、94,82 C、98,78 D、102,749. 记不等式组 表示的区域为 ,点 的坐标为 .有下面四个命题:
A、90,86 B、94,82 C、98,78 D、102,749. 记不等式组 表示的区域为 ,点 的坐标为 .有下面四个命题:, ; , ;
, ; , .
其中的真命题是( )
A、 , B、 , C、 , D、 ,10. 已知底面是正方形的直四棱柱 的外接球的表面积为 ,且 ,则 与底面 所成角的正切值为( )A、 B、 C、 D、11. 已知函数 ,设 , , ,则( )A、 B、 C、 D、12. 已知椭圆 的右焦点 关于直线 的对称点为 ,点 为 的对称中心,直线 的斜率为 ,且 的长轴不小于 ,则 的离心率( )A、存在最大值,且最大值为 B、存在最大值,且最大值为 C、存在最小值,且最小值为 D、存在最小值,且最小值为二、填空题
-
13. 若向量 与向量 共线,则 .14. 若函数 的最大值为 ,则 的最小正周期为 .
15. 现有如下假设:所有纺织工都是工会成员,部分梳毛工是女工,部分纺织工是女工,所有工会成员都投了健康保险,没有一个梳毛工投了健康保险.
下列结论可以从上述假设中推出来的是 . (填写所有正确结论的编号)
①所有纺织工都投了健康保险 ②有些女工投了健康保险 ③有些女工没有投健康保险 ④工会的部分成员没有投健康保险
16. 若函数 的最小值为 ,则 的取值范围为 .三、解答题
-
17. 设 为数列 的前 项和,已知 , .(1)、证明: 为等比数列;(2)、求 的通项公式,并判断 , , 是否成等差数列?18. 根据以往的经验,某建筑工程施工期间的降水量 (单位: )对工期的影响如下表:
降水量
工期延误天数
0
1
3
6
根据某气象站的资料,某调查小组抄录了该工程施工地某月前 天的降水量的数据,绘制得到降水量的折线图,如下图所示.
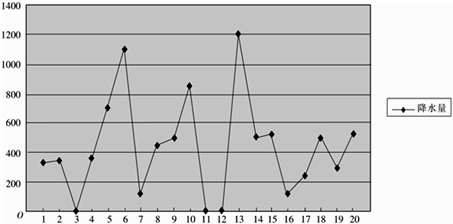 (1)、根据降水量的折线图,分别求该工程施工延误天数 的频率;(2)、以(1)中的频率作为概率,求工期延误天数 的分布列及数学期望与方差.19. 如图,在直三棱柱 中, , 为棱 的中点, .
(1)、根据降水量的折线图,分别求该工程施工延误天数 的频率;(2)、以(1)中的频率作为概率,求工期延误天数 的分布列及数学期望与方差.19. 如图,在直三棱柱 中, , 为棱 的中点, .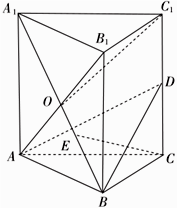 (1)、证明: 平面 ;(2)、设二面角 的正切值为 , , ,求异面直线 与 所成角的余弦值.20. 已知点 是抛物线 上一点,且 到 的焦点的距离为 .(1)、求抛物线 在点 处的切线方程;(2)、若 是 上一动点,且 不在直线 上,过 作直线 垂直于 轴且交 于点 ,过 作 的垂线,垂足为 .证明: 为定值,并求该定值.
(1)、证明: 平面 ;(2)、设二面角 的正切值为 , , ,求异面直线 与 所成角的余弦值.20. 已知点 是抛物线 上一点,且 到 的焦点的距离为 .(1)、求抛物线 在点 处的切线方程;(2)、若 是 上一动点,且 不在直线 上,过 作直线 垂直于 轴且交 于点 ,过 作 的垂线,垂足为 .证明: 为定值,并求该定值.