2017-2018学年浙教版八年级下学期数学期末模拟试卷（3）

试卷更新日期：2018-06-14 类型：期末考试

进入出卷网下载

一、选择题

1. 在函数 $y = \frac{\sqrt{x + 1}}{2 x - 1}$ 中，自变量x的取值范围是（）

A、x≥﹣1 B、x＞﹣1且x≠ $\frac{1}{2}$ C、x≥﹣1且x≠ $\frac{1}{2}$ D、x＞﹣1

查看试题解析
2. 等边三角形、平行四边形、矩形、菱形、正方形、正五边形中，既是轴对称图形，又是中心对称图形的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
3. 某超市一月份的营业额为200万元，三月份的营业额为288万元，如果每月比上一个月增长的百分数相同，则每月的平均增长率为（）

A、10% B、15% C、20% D、25%

查看试题解析
4. 如果一个三角形的三边长分别为1，k，3，则化简7− $\sqrt{4 k^{2} - 36 k + 81}$ −|2k−3|的结果是（　　）

A、-5 B、1 C、13 D、19-4k

查看试题解析
5. 如图．已知在正方形网格中，每个小方格都是边长为1的正方形，A、B两点在小方格的顶点上，位置如图所示，点C也在小方格的顶点上，且以A、B、C为顶点的三角形面积为1，则点C的个数为（）

A、3个 B、4个 C、5个 D、6个

查看试题解析
6. 用配方法解方程 $2 x^{2} - x - 1 = 0$ ，变形结果正确的是（）

A、 ${(x - \frac{1}{2})}^{2} = \frac{3}{4}$ B、 ${(x - \frac{1}{4})}^{2} = \frac{3}{4}$ C、 ${(x - \frac{1}{4})}^{2} = \frac{9}{16}$ D、 ${(x - \frac{1}{4})}^{2} = \frac{17}{16}$

查看试题解析
7. 已知下列命题：
①若a≠b，则a²≠b²；
②对于不为零的实数c，关于x的方程 $x + \frac{c}{a} = c + 1$ 的根是c．
③对角线互相垂直平分的四边形是菱形．
④过一点有且只有一条直线与已知直线平行．
⑤在反比例函数 $y = \frac{2}{x}$ 中，如果函数值y＜1时，那么自变量x＞2，是真命题的个数是（　　）

A、4个 B、3个 C、2个 D、1个

查看试题解析
8.
如图，M为双曲线y= $\frac{1}{x}$ 上的一点，过点M作x轴、y轴的垂线，分别交直线y=﹣x+m于D、C两点，若直线y=﹣x+m与y轴交于点A，与x轴相交于点B．则AD•BC的值为（　　）

A、1 B、2 C、3 D、4

查看试题解析
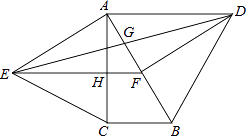
9. 如图1，在矩形MNPO中，动点R从点N出发，沿N→P→O→M方向运动至点M处停止．设点R运动的路程为x，△MNR的面积为y，如果y关于x的函数图象如图2所示，则矩形MNPO的周长是（）

A、11 B、15 C、16 D、24

查看试题解析
10. 如图，分别以直角△ABC的斜边AB，直角边AC为边向△ABC外作等边△ABD和等边△ACE，F为AB的中点，DE与AB交于点G，EF与AC交于点H，∠ACB=90°，∠BAC=30°．给出如下结论：
①EF⊥AC；②四边形ADFE为菱形；③AD=4AG；④FH= $\frac{1}{4}$ BD；
其中正确结论的是（）

A、①②③ B、①②④ C、①③④ D、②③④

查看试题解析

二、填空题

11. 已知 $x^{2} + x - 1 = 0$ ，那么代数式 $x^{3} + 2 x^{2} - 7$ 的值为.

查看试题解析
12. 计算：（ $\sqrt{5}$ ﹣2）²⁰¹⁶×（ $\sqrt{5}$ +2）²⁰¹⁷= ．

查看试题解析
13. 对于整数a、b、c、d，符号 $| \begin{matrix} a & b \\ d & c \end{matrix} |$ 表示运算ac﹣bd，已知1＜ $| \begin{matrix} 1 & b \\ d & 4 \end{matrix} |$ ＜4，则乘积bd的整数解个数是．

查看试题解析
14. 如图，将两张长为4，宽为1的矩形纸条交叉并旋转，使重叠部分成为一个菱形．旋转过程中，当两张纸条垂直时，菱形周长的最小值是4，那么菱形周长的最大值是．

查看试题解析
15. 如图，已知在Rt△ABC中，D是斜边AB的中点，AC=4，BC=2，将△ACD沿直线CD折叠，点A落在点E处，联结AE，那么线段AE的长度等于．

查看试题解析
16. 如图，已知△ABC的周长为a，A₁B₁ ， B₁C₁ ， A₁C₁是△ABC的三条中位线，它们构成了△A₁B₁C₁ ， △A₂B₂C₂是由△A₁B₁C₁的三条中位线A₂B₂ ， B₂C₂ ， A₂C₂构成的……如此进行下去，得到△A_nB_nC_n ，则△A₁B₁C₁的周长为， △A₂B₂C₂的周长为， △A₃B₃C₃的周长为， △A_nB_nC_n的周长为．

查看试题解析

三、解答题

17. 解方程：解一元二次方程

(1)、(x＋1)²＝9

(2)、x²－4x＋2＝0

查看试题解析
18. 已知：如图，在△ABC中，D是BC边上的一点，E是AD的中点，过点A作BC的平行线交于BE的延长线于点F，且AF=DC，连接CF．

(1)、求证：D是BC的中点；

(2)、如果AB=AC，试判断四边形ADCF的形状，并证明你的结论．

查看试题解析
19. 某厂按用户的月需求量x（件）完成一种产品的生产，其中x＞0，每件的售价为18万元，每件的成本y（万元）是基础价与浮动价的和，其中基础价保持不变，浮动价与月需求量x（件）成反比，经市场调研发现，月需求量x与月份n（n为整数，1≤n≤12），符合关系式x=2n²﹣2kn+9（k+3）（k为常数），且得到了表中的数据．
月份n（月）
1
2
成本y（万元/件）
11
12
需求量x（件/月）
120
100

(1)、求y与x满足的关系式，请说明一件产品的利润能否是12万元；

(2)、求k，并推断是否存在某个月既无盈利也不亏损；

(3)、在这一年12个月中，若第m个月和第（m+1）个月的利润相差最大，求m．

查看试题解析
20.
如图1，在矩形纸片ABCD中，AB=3cm，AD=5cm，折叠纸片使B点落在边AD上的E处，折痕为PQ，过点E作EF∥AB交PQ于F，连接BF．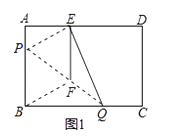

(1)、求证：四边形BFEP为菱形；

(2)、
当点E在AD边上移动时，折痕的端点P、Q也随之移动；
①当点Q与点C重合时（如图2），求菱形BFEP的边长；
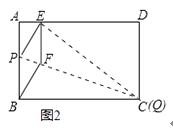
②若限定P、Q分别在边BA、BC上移动，求出点E在边AD上移动的最大距离．

查看试题解析
21. 在平面直角坐标系中，正方形OABC的顶点O在原点。

(1)、如图①，点C的坐标为（ $a$ ， $b$ ），且实数 $a$ ， $b$ 满足 $a = \sqrt{(b - 3)} + \sqrt{(3 - b)} - 1$ ，求C点的坐标及线段OC的长度；

(2)、如图②，点F在BC上，AB交x轴于点E，EF，OC的延长线交于点G，EG=OG，求∠EOF的度数；

(3)、如图③，将（1）中正方形OABC绕点O顺时针旋转，使OA落在y轴上，E为AB上任意一点，OE的垂直平分线交x轴于点G，交OE于点P，连接EG交BC于点F，求△BEF的周长。

查看试题解析
22.
如图，在平面直角坐标系 $xOy$ 中，已知四边形DOBC是矩形，且D（0，4），B（6，0）．若反比例函数 $y = \frac{k_{1}}{x}$ （ $x$ ＞0）的图象经过线段OC的中点A（3，2），交DC于点E，交BC于点F．设直线EF的解析式为 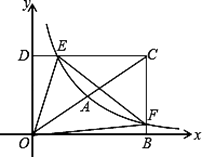$y = k_{2} x + b$ ．

(1)、求反比例函数和直线EF的解析式；

(2)、求△OEF的面积；

(3)、请结合图象直接写出不等式 $k_{2} x + b - \frac{k_{1}}{x}$ ＞0的解集．

查看试题解析

月份n（月）	1	2
成本y（万元/件）	11	12
需求量x（件/月）	120	100