2017-2018学年浙教版八年级下学期数学期末模拟试卷(2)
试卷更新日期:2018-06-14 类型:期末考试
一、选择题
-
1. 关于x的一元二次方程x2+ax﹣1=0的根的情况是( )A、没有实数根 B、只有一个实数根 C、有两个相等的实数根 D、有两个不相等的实数根2. 已知 ,则化简 的结果是( )
A、4 B、 C、 D、3. 下列说法正确的是( )A、打开电视,它正在播广告是必然事件 B、要考察一个班级中的学生对建立生物角的看法适合用抽样调查 C、在抽样调查过程中,样本容量越大,对总体的估计就越准确 D、甲、乙两人射中环数的方差分别为S甲2=2,S乙2=4,说明乙的射击成绩比甲稳定4. 如图,E,F分别是▱ABCD的边AD、BC上的点,EF=6,∠DEF=60°,将四边形EFCD沿EF翻折,得到EFC′D′,ED′交BC于点G,则△GEF的周长为( ) A、6 B、12 C、18 D、245. 如图,在正方形ABCD中,AB=9,点E在CD边上,且DE=2CE,点P是对角线AC上的一个动点,则PE+PD的最小值是( )
A、6 B、12 C、18 D、245. 如图,在正方形ABCD中,AB=9,点E在CD边上,且DE=2CE,点P是对角线AC上的一个动点,则PE+PD的最小值是( ) A、3 B、10 C、9 D、96. 平面直角坐标系xOy中,如果有点P(﹣2,1)与点Q(2,﹣1),那么:①点P与点Q关于x轴对称;②点P与点Q关于y轴对称;③点P与点Q关于原点对称;④点P与点Q都在y=-的图象上,前面的四种描述正确的是( )
A、3 B、10 C、9 D、96. 平面直角坐标系xOy中,如果有点P(﹣2,1)与点Q(2,﹣1),那么:①点P与点Q关于x轴对称;②点P与点Q关于y轴对称;③点P与点Q关于原点对称;④点P与点Q都在y=-的图象上,前面的四种描述正确的是( )
A、①② B、②③ C、①④ D、③④7. 已知 是正整数,则实数n的最大值为( )A、12 B、11 C、8 D、38. 如图,点A在双曲线y=的第一象限的那一支上,AB垂直于y轴于点B,点C在x轴正半轴上,且OC=2AB,点E在线段AC上,且AE=3EC,点D为OB的中点,若△ADE的面积为3,则k的值为( )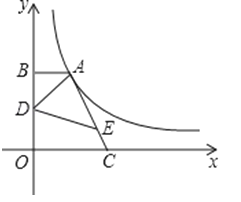 A、16 B、 C、 D、99. 若关于x的一元二次方程(k+1)x2+2(k+1)x+k﹣2=0有实数根,则k的取值范围在数轴上表示正确的是( )A、
A、16 B、 C、 D、99. 若关于x的一元二次方程(k+1)x2+2(k+1)x+k﹣2=0有实数根,则k的取值范围在数轴上表示正确的是( )A、 B、
B、 C、
C、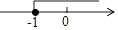 D、
D、 10. 如图是某城市部分街道的示意图,AF∥BC,EC⊥BC,AB∥DE,BD∥AE,甲、乙两人同时从B站乘车到F站,甲乘1路车,路线是B→A→E→F;乙乘2路车,路线是B→D→C→F.假定两车的速度相同,那么( )先到达F站.
10. 如图是某城市部分街道的示意图,AF∥BC,EC⊥BC,AB∥DE,BD∥AE,甲、乙两人同时从B站乘车到F站,甲乘1路车,路线是B→A→E→F;乙乘2路车,路线是B→D→C→F.假定两车的速度相同,那么( )先到达F站.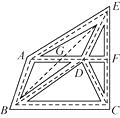 A、两人同时到达F站 B、甲 C、乙 D、无法判断
A、两人同时到达F站 B、甲 C、乙 D、无法判断二、填空题
-
11. 有一人患了流感,经过两轮传染后共有 人患了流感,每轮传染中平均一个人传染了人.
12. 若 =-a,则a应满足的条件是 .13. 高一新生入学军训射击训练中,小张同学的射击成绩(单位:环)为:5、7、9、10、7,则这组数据的众数是 .14. 已知关于x的一次函数y=mx+n的图象如图所示,则 可化简为 . 15. 如图,将正方形OABC放在平面直角坐标系中,O是原点,A的坐标为(1, ),则点C的坐标为 .
15. 如图,将正方形OABC放在平面直角坐标系中,O是原点,A的坐标为(1, ),则点C的坐标为 . 16. 如图,点A、B在反比例函数y= (k>0,x>0)的图象上,过点A、B作x轴的垂线,垂足分别为M、N,延长线段AB交x轴于点C,若OM=MN=NC,△AOC的面积为6,则k的值为 .
16. 如图,点A、B在反比例函数y= (k>0,x>0)的图象上,过点A、B作x轴的垂线,垂足分别为M、N,延长线段AB交x轴于点C,若OM=MN=NC,△AOC的面积为6,则k的值为 .
三、解答题
-
17. 已知, , ,求 的值。
18. 如图,为美化环境,某小区计划在一块长方形空地上修建一个面积为1500平方米的长方形草坪,并将草坪四周余下的空地修建成同样宽的通道,已知长方形空地的长为60米,宽为40米.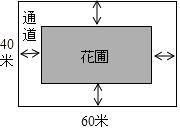 (1)、求通道的宽度;(2)、晨光园艺公司承揽了该小区草坪的种植工程,计划种植“四季青”和“黑麦草”两种绿草,该公司种植“四季青”的单价是30元/平方米,超过50平方米后,每多出5平方米,所有“四季青”的种植单价可降低1元,但单价不低于20元/平方米,已知小区种植“四季青”的面积超过了50平方米,支付晨光园艺公司种植“四季青”的费用为2000元,求种植“四季青”的面积.19. 为了倡导“节约用水,从我做起”,黄冈市政府决定对市直机关500户家庭的用水情况作一次调查,市政府调查小组随机抽查了其中100户家庭一年的月平均用水量(单位:吨).并将调查结果制成了如图所示的条形统计图.
(1)、求通道的宽度;(2)、晨光园艺公司承揽了该小区草坪的种植工程,计划种植“四季青”和“黑麦草”两种绿草,该公司种植“四季青”的单价是30元/平方米,超过50平方米后,每多出5平方米,所有“四季青”的种植单价可降低1元,但单价不低于20元/平方米,已知小区种植“四季青”的面积超过了50平方米,支付晨光园艺公司种植“四季青”的费用为2000元,求种植“四季青”的面积.19. 为了倡导“节约用水,从我做起”,黄冈市政府决定对市直机关500户家庭的用水情况作一次调查,市政府调查小组随机抽查了其中100户家庭一年的月平均用水量(单位:吨).并将调查结果制成了如图所示的条形统计图. (1)、请将条形统计图补充完整;(2)、求这100个样本数据的平均数,众数和中位数;(3)、根据样本数据,估计黄冈市直机关500户家庭中月平均用水量不超过12吨的约有多少户?20. 如图,在平面直角坐标系中,直线l:y=﹣ x+4与x轴、y轴分别交于点M,N,高为3的等边三角形ABC,边BC在x轴上,将此三角形沿着x轴的正方向平移,在平移过程中,得到△A1B1C1 , 当点B1与原点重合时,解答下列问题:
(1)、请将条形统计图补充完整;(2)、求这100个样本数据的平均数,众数和中位数;(3)、根据样本数据,估计黄冈市直机关500户家庭中月平均用水量不超过12吨的约有多少户?20. 如图,在平面直角坐标系中,直线l:y=﹣ x+4与x轴、y轴分别交于点M,N,高为3的等边三角形ABC,边BC在x轴上,将此三角形沿着x轴的正方向平移,在平移过程中,得到△A1B1C1 , 当点B1与原点重合时,解答下列问题: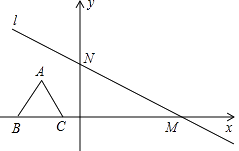 (1)、求出点A1的坐标,并判断点A1是否在直线l上;(2)、求出边A1C1所在直线的解析式;(3)、在坐标平面内找一点P,使得以P、A1、C1、M为顶点的四边形是平行四边形,请直接写出P点坐标.21. 如图,在矩形纸片ABCD中,AB=4,AD=12,将矩形纸片折叠,使点C落在AD边上的点M处,折痕为PE,此时PD=3.
(1)、求出点A1的坐标,并判断点A1是否在直线l上;(2)、求出边A1C1所在直线的解析式;(3)、在坐标平面内找一点P,使得以P、A1、C1、M为顶点的四边形是平行四边形,请直接写出P点坐标.21. 如图,在矩形纸片ABCD中,AB=4,AD=12,将矩形纸片折叠,使点C落在AD边上的点M处,折痕为PE,此时PD=3. (1)、求MP的值;
(1)、求MP的值;
(2)、在AB边上有一个动点F,且不与点A,B重合.当AF等于多少时,△MEF的周长最小?(3)、若点G,Q是AB边上的两个动点,且不与点A,B重合,GQ=2.当四边形MEQG的周长最小时,求最小周长值.(计算结果保留根号)22. 如图,一次函数y=﹣x+b与反比例函数y= (k≠0)的图象相交于A(﹣1,4)、B(4,﹣1)两点,直线l⊥x轴于点E(﹣4,0),与反比例函数和一次函数的图象分别相交于点C、D,连接AC、BC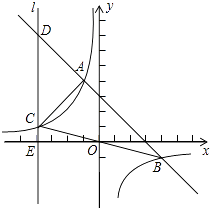 (1)、求出b和k;(2)、求证:△ACD是等腰直角三角形;(3)、在y轴上是否存在点P,使S△PBC=S△ABC?若存在,请求出P的坐标;若不存在,请说明理由.
(1)、求出b和k;(2)、求证:△ACD是等腰直角三角形;(3)、在y轴上是否存在点P,使S△PBC=S△ABC?若存在,请求出P的坐标;若不存在,请说明理由.