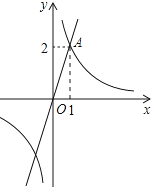2017-2018学年浙教版八年级下学期数学期末模拟试卷(1)
试卷更新日期:2018-06-14 类型:期末考试
一、选择题
-
1. 在一次中学生田径运动会上,参加男子跳高的15名运动员的成绩如表:这些运动员跳高成绩的中位数和众数分别是( )
跳高成绩(m)
1.50
1.55
1.60
1.65
1.70
1.75
跳高人数
1
3
2
3
5
1
A、1.65,1.70 B、1.70,1.65 C、1.70,1.70 D、3,52. 下列图形中既是轴对称图形又是中心对称图形的是( )
A、 B、
B、 C、
C、 D、
D、 3. 如果一个多边形的内角和等于它的外角和的2倍,则这个多边形是( )A、三角形 B、四边形 C、五边形 D、六边形4. 若关于x的方程x2+2x﹣a=0有两个相等的实数根,则a的值为( )A、﹣1 B、1 C、﹣4 D、45. 下列性质中,正方形具有而矩形不一定具有的性质是( )A、对角线互相垂直 B、对角线互相平分 C、对角线相等 D、四个角都是直角6. 反比例函数y= 的图象经过点A(﹣1,2),则当x>1时,函数值y的取值范围是( )
3. 如果一个多边形的内角和等于它的外角和的2倍,则这个多边形是( )A、三角形 B、四边形 C、五边形 D、六边形4. 若关于x的方程x2+2x﹣a=0有两个相等的实数根,则a的值为( )A、﹣1 B、1 C、﹣4 D、45. 下列性质中,正方形具有而矩形不一定具有的性质是( )A、对角线互相垂直 B、对角线互相平分 C、对角线相等 D、四个角都是直角6. 反比例函数y= 的图象经过点A(﹣1,2),则当x>1时,函数值y的取值范围是( )
A、y>﹣1 B、﹣1<y<0 C、y<﹣2 D、﹣2<y<07. 将矩形纸片ABCD按如图所示的方式折叠,恰好得到菱形AECF.若AB=3,则菱形AECF的面积为( )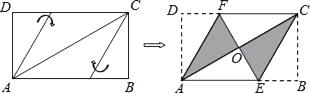 A、1 B、 C、 D、48. 如图所示,将长方形纸片先沿虚线AB向右对折,接着将对折后的纸片沿虚线CD向下对折,然后剪下一个小三角形,再将纸片打开,则打开后的展形图是( )
A、1 B、 C、 D、48. 如图所示,将长方形纸片先沿虚线AB向右对折,接着将对折后的纸片沿虚线CD向下对折,然后剪下一个小三角形,再将纸片打开,则打开后的展形图是( )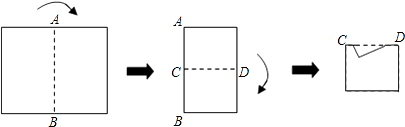 A、
A、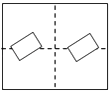 B、
B、 C、
C、 D、
D、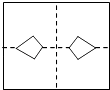 9. 由于国家出台对房屋的限购令,我省某地的房屋价格原价为8400元/米2 , 通过连续两次降价a%后,售价变为6000元/米2 , 下列方程中正确的是( )A、8400(1-a%2)=6000 B、6000(1-a%2)=8400 C、8400(1+a%)2=6000 D、8400(1-a%)2=600010. 如图,P为正方形ABCD的对角线BD上任一点,过点P作PE⊥BC于点E,PF⊥CD于点F,连接EF.给出以下4个结论:①△FPD是等腰直角三角形;②AP=EF;③AD=PD;④∠PFE=∠BAP.其中,所有正确的结论是( )
9. 由于国家出台对房屋的限购令,我省某地的房屋价格原价为8400元/米2 , 通过连续两次降价a%后,售价变为6000元/米2 , 下列方程中正确的是( )A、8400(1-a%2)=6000 B、6000(1-a%2)=8400 C、8400(1+a%)2=6000 D、8400(1-a%)2=600010. 如图,P为正方形ABCD的对角线BD上任一点,过点P作PE⊥BC于点E,PF⊥CD于点F,连接EF.给出以下4个结论:①△FPD是等腰直角三角形;②AP=EF;③AD=PD;④∠PFE=∠BAP.其中,所有正确的结论是( ) A、①② B、①④ C、①②④ D、①③④
A、①② B、①④ C、①②④ D、①③④二、填空题
-
11. 七边形的内角和是度.12. 计算:( + )× = .13. 如果关于x的一元二次方程kx2﹣x+1=0有两个不相等的实数根,那么k的取值范围是14. 在﹣1、3、﹣2这三个数中,任选两个数的积作为k的值,使反比例函数 的图象在第一、三象限的概率是 .15. 如图,菱形OABC的一边OA在x轴的负半轴上,O是坐标原点,tan∠AOC= ,反比例函数y= 的图象经过点C,与AB交于点D,若△COD的面积为20,则k的值等于 .
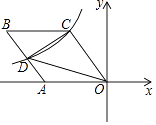 16. 如图,在▱ABCD中,AM= AD,BD与MC相交于点O,则S△MOD:S△COD= .
16. 如图,在▱ABCD中,AM= AD,BD与MC相交于点O,则S△MOD:S△COD= .
三、解答题
-
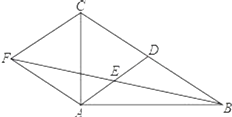
17. 已知a=2+ ,b=2- ,求a2-2ab+b2的值.18. 某商场将每件进价为80元的某种商品原来按每件100元出售,一天可售出100件.后来经过市场调查,发现这种商品单价每降低1元,其销量可增加10件.(1)、求商场经营该商品原来一天可获利润多少元?(2)、若商场经营该商品一天要获利润2160元,并让顾客得到实惠,则每件商品应降价多少元?19. 若x1、x2是方程x2+2(m﹣2)x+m2+4=0的两个实数根,且x12+x22﹣x1x2=21,求m的值.20. 已知:如图,四边形ABCD中,AD∥BC,AD=CD,E是对角线BD上一点,且EA=EC.
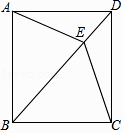 (1)、求证:四边形ABCD是菱形;(2)、如果BE=BC,且∠CBE:∠BCE=2:3,求证:四边形ABCD是正方形.
(1)、求证:四边形ABCD是菱形;(2)、如果BE=BC,且∠CBE:∠BCE=2:3,求证:四边形ABCD是正方形.