2017-2018学年北师大版八年级下学期数学期末模拟试卷（1）

试卷更新日期：2018-06-14 类型：期末考试

进入出卷网下载

一、选择题

1. 下列图案中，是轴对称图形但不是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列等式从左到右的变形，属于因式分解的是（　　）

A、a（x﹣y）=ax﹣ay B、x²+2x+1=x（x+2）+1 C、（x+1）（x+3）=x²+4x+3 D、x³﹣x=x（x+1）（x﹣1）

查看试题解析
3.
如图，△ABC中，AB=5，AC=6，BC=4，边AB的垂直平分线交AC于点D，则△BDC的周长是（　　）

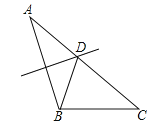A、8 B、9 C、10 D、11

查看试题解析
4. 如图，在Rt△ABC中，∠C=90°，∠A=30°，AB+BC=12cm，则AB等于（）

A、6 cm B、7 cm C、8 cm D、9 cm

查看试题解析
5. 不等式组 ${\begin{matrix} 2 - x \geq 3 \\ \frac{3}{2} x + 1 > x - \frac{3}{2} \end{matrix}$ 的解集在数轴上表示正确的是（）

A、 B、 C、 D、

查看试题解析
6. 如图，△ABC的面积为12，将△ABC沿BC方向移到△A′B′C′的位置，使B′与C重合，连接AC′交A′C于D，则△C′DC的面积为（）

A、10 B、8 C、6 D、4

查看试题解析
7. 小敏不慎将一块平行四边形玻璃打碎成如图的四块，为了能在商店配到一块与原来相同的平行四边形玻璃，他带了两块碎玻璃，其编号应该是（）

A、①，② B、①，④ C、③，④ D、②，③

查看试题解析
8. 若关于x的方程 $\frac{a x}{x - 2}$ = $\frac{4}{x - 2}$ +1无解，则a的值为（）

A、1 B、2 C、1或2 D、0或2

查看试题解析
9. 对于实数a，b，现用“☆”定义新运算：a☆b＝a³－ab，那么将多项式a☆4因式分解，其结果为( )

A、a(a＋2)(a－2) B、a(a＋4)(a－4) C、(a＋4)(a－4) D、a(a²＋4)

查看试题解析
10. 某种商品的进价为160元，出售时的标价为240元，后来由于该商品积压，商店准备打折出售，但要保持利润不低于5%，则至多可打（）

A、6折 B、7折 C、8折 D、9折

查看试题解析
11. 已知关于x的分式方程 $\frac{3 x - a}{x - 3}$ = $\frac{1}{3}$ 的解是非负数，那么a的取值范围是（）

A、a＞1 B、a≥1 C、a≥1且a≠9 D、a≤1

查看试题解析
12. 如图，在▱ABCD中，对角线AC的垂直平分线分别交AD，BC于点E，F，连接CE，若△CED的周长为6，则▱ABCD的周长为（）

A、6 B、12 C、18 D、24

查看试题解析

二、填空题

13. 因式分解：a²b﹣4ab+4b= ．

查看试题解析
14. 不等式2x+1＞0的解集是．

查看试题解析
15. 方程 $\frac{2}{x - 4} - \frac{1 - x}{4 - x} = 0$ 的解是．

查看试题解析
16. 如图，将平行四边形ABCD沿对角线BD折叠，使点A落在点A'处．若∠1=∠2=50°，则∠A'为．

查看试题解析
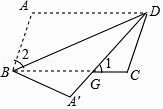17. 两个全等的三角尺重叠放在△ACB的位置，将其中一个三角尺绕着点C按逆时针方向旋转至△DCE的位置，使点A恰好落在边DE上，AB与CE相交于点F．已知∠ACB=∠DCE=90°，∠B=30°，AB=8cm，则CF=cm．

查看试题解析
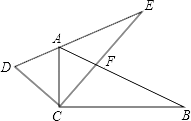18.
如图，在△ABC中，∠ACB=90°，M、N分别是AB、AC的中点，延长BC至点D，使CD= $\frac{1}{3}$ BD，连接DM、DN、MN．若AB=6，则DN= ．

查看试题解析

三、解答题

19. 解答题

(1)、解方程： $x^{2} - 3 x - 1 = 0$ ；

(2)、解不等式组： ${\begin{cases} 3 (x + 1) < 5 x① \\ \frac{1}{3} x - 1 \leq 7 - \frac{5}{3} x② \end{cases}$

查看试题解析
20. 解分式方程： $\frac{10 x}{2 x- 1} + \frac{5}{1 - 2 x} = 2$

查看试题解析
21. 杨梅是漳州的特色时令水果，杨梅一上市，水果店的老板用1200元购进一批杨梅，很快售完；老板又用2500元购进第二批杨梅，所购件数是第一批的2倍，但进价比第一批每件多了5元．

(1)、第一批杨梅每件进价多少元？

(2)、老板以每件150元的价格销售第二批杨梅，售出80%后，为了尽快售完，决定打折促销，要使第二批杨梅的销售利润不少于320元，剩余的杨梅每件售价至少打几折？（利润=售价﹣进价）

查看试题解析
22. 由于雾霾天气频发，市场上防护口罩出现热销．某药店准备购进一批口罩，已知1个A型口罩和3个B型口罩共需26元；3个A型口罩和2个B型口罩共需29元．

(1)、求一个A型口罩和一个B型口罩的售价各是多少元？

(2)、药店准备购进这两种型号的口罩共50个，其中A型口罩数量不少于35个，且不多于B型口罩的3倍，有哪几种购买方案，哪种方案最省钱？

查看试题解析
23. 图①、图②、图③都是由边长为1的小等边三角形构成的网格，每个小等边三角形的顶点称为格点．线段AB的端点在格点上．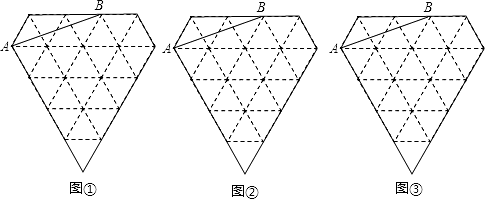

(1)、在图①、图2中，以AB为边各画一个等腰三角形，且第三个顶点在格点上；（所画图形不全等）

(2)、在图③中，以AB为边画一个平行四边形，且另外两个顶点在格点上．

查看试题解析
24.
如图，BD是△ABC的角平分线，点E，F分别在BC，AB上，且DE∥AB，EF∥AC．
（1）求证：BE=AF；
（2）若∠ABC=60°，BD=12，求DE的长及四边形ADEF的面积．

查看试题解析
25.
如图，四边形ABCD为平行四边形，∠BAD的角平分线AE交CD于点F，交BC的延长线于点E．

(1)、求证：BE=CD；

(2)、连接BF，若BF⊥AE，∠BEA=60°，AB=4，求平行四边形ABCD的面积．

查看试题解析
26.
在平面直角坐标系中，O为原点，点A（4，0），点B（0，3），把△ABO绕点B逆时针旋转，得△A′BO′，点A，O旋转后的对应点为A′，O′，记旋转角为α．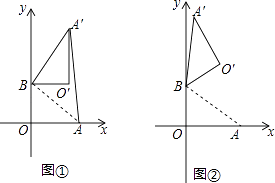

(1)、如图①，若α=90°，求AA′的长；

(2)、如图②，若α=120°，求点O′的坐标；

(3)、在（2）的条件下，边OA上的一点P旋转后的对应点为P′，当O′P+BP′取得最小值时，求点P′的坐标（直接写出结果即可）

查看试题解析