2017-2018学年人教版八年级下学期数学期末模拟试卷（3）

试卷更新日期：2018-06-14 类型：期末考试

进入出卷网下载

一、选择题

1. 若 $\sqrt{a - 3}$ 在实数范围内有意义，则n的取值范围是（）

A、a>3 B、a<3 C、a≥3 D、a≤3

查看试题解析
2. 在△ABC中，AB=8，AC=15，BC=17，则该三角形为（　　）

A、锐角三角形 B、直角三角形 C、钝角三角形 D、等腰直角三角形

查看试题解析
3. 计算 $\sqrt{12} (\sqrt{75} + 3 \sqrt{\frac{1}{3}} - \sqrt{48})$ 的结果是（）

A、6 B、 $4 \sqrt{3}$ C、 $2 \sqrt{3} + 6$ D、12

查看试题解析
4. 下列性质中菱形不一定具有的性质是（）

A、对角线互相平分 B、对角线互相垂直 C、对角线相等 D、既是轴对称图形又是中心对称图形

查看试题解析
5. 某校数学兴趣小组在一次数学课外活动中，随机抽查该校10名同学参加今年初中学业水平考试的体育成绩，得到结果如下表所示：
成绩/分
36
37
38
39
40
人数/人
1
2
1
4
2
下列说法正确的是（）

A、这10名同学体育成绩的中位数为38分 B、这10名同学体育成绩的平均数为38分 C、这10名同学体育成绩的众数为39分 D、这10名同学体育成绩的方差为2

查看试题解析
6. 如图，正方形ABCD中，E为DC边上一点，且DE=1，AE=EF，∠AEF=90°，则FC= （）

A、 $\sqrt{3}$ B、 $\sqrt{2}$ C、 $\frac{\sqrt{3}}{2}$ D、1

查看试题解析
7. 在一次数学测试中，某学习小组6名同学的成绩（单位：分）分别为65，82，86，82，76，95．关于这组数据，下列说法错误的是（）

A、众数是82 B、中位数是82 C、极差是30 D、平均数是82

查看试题解析
8. 已知正比例函数y=kx（k≠0），点（2，-3）在函数上，则y随x的增大而（　　）

A、增大 B、减小 C、不变 D、不能确定

查看试题解析
9. 如图，是一张平行四边形纸片ABCD，要求利用所学知识将它变成一个菱形，甲、乙两位同学的作法分别如下：对于甲、乙两人的作法，可判断（）

A、甲、乙均正确 B、甲、乙均错误 C、甲正确，乙错误 D、甲错误，乙正确

查看试题解析
10. 已知三角形的三边长分别为a、b、c，求其面积问题，中外数学家曾经进行过深入研究，古希腊的几何学家海伦（Heron，约公元50年）给出求其面积的海伦公式S= $\sqrt{p (p - a) (p - b) (p - c)}$ ，其中p= $\frac{a + b + c}{2}$ ；我国南宋时期数学家秦九韶（约1202﹣1261）曾提出利用三角形的三边求其面积的秦九韶公式S= $\frac{1}{2} \sqrt{a^{2} b^{2} - {(\frac{a^{2} + b^{2} - c^{2}}{2})}^{2}}$ ，若一个三角形的三边长分别为2，3，4，则其面积是（）

A、 $\frac{3 \sqrt{15}}{8}$ B、 $\frac{3 \sqrt{15}}{4}$ C、 $\frac{3 \sqrt{15}}{2}$ D、 $\frac{\sqrt{15}}{2}$

查看试题解析
11.
如图，在矩形ABCD中，AB=5，BC=7，点E是AD上一个动点，把△BAE沿BE向矩形内部折叠，当点A的对应点A₁恰好落在∠BCD 的平分线上时，CA₁的长为（　　）

A、3或4 $\sqrt{2}$ B、4或3 $\sqrt{2}$ C、3或4 D、3 $\sqrt{2}$ 或4 $\sqrt{2}$

查看试题解析
12. 如图，在平面直角坐标系中，正方形ABCD的边长为1，AD边的中点处有一动点P，动点P沿P→A→B→C→D→P运动一周，则点P的纵坐标y与点P走过的路程x之间的函数关系用图象表示大致是（）

A、 B、 C、 D、

查看试题解析

二、填空题

13. 计算： $\sqrt{{(- 3)}^{2}}$ = ．

查看试题解析
14. 一组数据1，4，6，x的中位数和平均数相等，则x的值是 .

查看试题解析
15.
如图，小聪与小慧玩跷跷板，跷跷板支架高EF为0.6米，E是AB的中点，那么小聪能将小慧翘起的最大高度BC等于米．

查看试题解析
16. 如图，矩形ABCD中，AB=3，AD=1，AB在数轴上，若以点A为圆心，对角线AC的长为半径作弧交数轴的正半轴于M，则点M的表示的数为

查看试题解析
17.
如图，点A、B的坐标分别为（0，3）、（4，6），点P为x轴上的一个动点，若点B关于直线AP的对称点B′恰好落在坐标轴上，则点B′的坐标为

查看试题解析

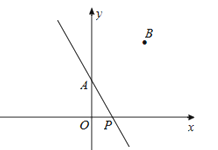
三、解答题

18. 计算

(1)、 $\sqrt[3]{- 8}$ + $\sqrt{6}$ ×（ $\sqrt{2} + \sqrt{\frac{2}{3}}$ ）

(2)、 $\frac{\sqrt{12} + \sqrt{27}}{\sqrt{3}}$ -（ $\sqrt{3} - \sqrt{2}$ ）²+ $| - \sqrt{6} |$

查看试题解析
19.
如图，平行四边形ABCD的对角线AC和BD相交于点O ， E ， F分别为OB ， OD的中点，过点O任作一直线分别交AB ， CD于点G ， H.
试说明：GF∥EH.

查看试题解析
20. 如图，已知四边形ABCD是菱形，点M、N分别在AB、AD上，且BM=DN，MG∥AD，NF∥AB，点F、G分别在BC、CD上，MG与NF相交于点E，求证：四边形AMEN是菱形．

查看试题解析
21.
某校八年级共有四个班，各班的人数如图1所示，人数比例如图2所示．

(1)、试求出该校八年级的学生总人数；

(2)、请补充条形统计表；

(3)、在一次数学考试中，1班、2班、3班、4班的平均成绩分别为92分、91分、90分、95分．试求出该校八年级学生在本次数学考试的平均分．

查看试题解析
22. 如图，已知直线y=kx+b经过点A(1，4)，B(0，2)，与x轴交于点C ，经过点D(1，0)的直线DE平行于OA ，并与直线AB交于点E ．

(1)、求直线AB的解析式；

(2)、求直线DE的解析式；

(3)、求△EDC的面积．

查看试题解析
23.
如图，在△ABC中，AB=AC，∠DAC是△ABC的一个外角．
实验与操作：
根据要求进行尺规作图，并在图中标明相应字母（保留作图痕迹，不写作法）
（1）作∠DAC的平分线AM；
（2）作线段AC的垂直平分线，与AM交于点F，与BC边交于点E，连接AE，CF．
猜想并证明：
判断四边形AECF的形状并加以证明．

查看试题解析
24.
如图，在平面直角坐标系中，直线AB与x轴、y轴的正半轴分别交于点A，B，直线CD与x轴正半轴、y轴负半轴分别交于点D，C，AB与CD相交于点E，点A，B，C，D的坐标分别为（8，0）、（0，6）、（0，﹣3）、（4，0），点M是OB的中点，点P在直线AB上，过点P作PQ∥y轴，交直线CD于点Q，设点P的横坐标为m．

(1)、求直线AB，CD对应的函数关系式；

(2)、用含m的代数式表示PQ的长；

(3)、若以点M，O，P，Q为顶点的四边形是矩形，请直接写出相应的m的值．

查看试题解析
25. 在平面直角坐标系中，正方形OABC的顶点O在原点。

(1)、如图①，点C的坐标为（ $a$ ， $b$ ），且实数 $a$ ， $b$ 满足 $a = \sqrt{(b - 3)} + \sqrt{(3 - b)} - 1$ ，求C点的坐标及线段OC的长度；

(2)、如图②，点F在BC上，AB交x轴于点E，EF，OC的延长线交于点G，EG=OG，求∠EOF的度数；

(3)、如图③，将（1）中正方形OABC绕点O顺时针旋转，使OA落在y轴上，E为AB上任意一点，OE的垂直平分线交x轴于点G，交OE于点P，连接EG交BC于点F，求△BEF的周长。

查看试题解析

成绩/分	36	37	38	39	40
人数/人	1	2	1	4	2