2017-2018学年人教版八年级下学期数学期末模拟试卷(2)
试卷更新日期:2018-06-14 类型:期末考试
一、选择题
-
1. 下列计算正确的是( )A、 - = B、( )-1=- C、 ÷ =2 D、3 - =32. 下列说法中不成立的是( )A、在y=3x﹣1中y+1与x成正比例 B、在y=﹣ 中y与x成正比例 C、在y=2(x+1)中y与x+1成正比例 D、在y=x+3中y与x成正比例3. 为了解某班学生双休户外活动情况,对部分学生参加户外活动的时间进行抽样调查,结果如下表:
户外活动的时间(小时)
1
2
3
6
学生人数(人)
2
2
4
2
则关于“户外活动时间”这组数据的众数、中位数、平均数分别是( )
A、3、3、3 B、6、2、3 C、3、3、2 D、3、2、34. 直角三角形两条直角边的长分别为3和4,则此直角三角形斜边上的中线长为( )
A、1.5 B、2 C、5 D、2.55. 如图,在△ABC中,∠C=90°,AC=2,点D在BC上,∠ADC=2∠B,AD= , 则BC的长为( ) A、-1 B、+1 C、-1 D、+16. 顺次连接矩形的四边形中点所得的四边形一定是( )A、平行四边形 B、矩形 C、菱形 D、正方形7. 如图,直线y=ax+b过点A(0,2)和点B(﹣3,0),则方程ax+b=0的解是( )
A、-1 B、+1 C、-1 D、+16. 顺次连接矩形的四边形中点所得的四边形一定是( )A、平行四边形 B、矩形 C、菱形 D、正方形7. 如图,直线y=ax+b过点A(0,2)和点B(﹣3,0),则方程ax+b=0的解是( )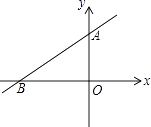 A、x=2 B、x=0 C、x=﹣1 D、x=﹣38. 如图,▱ABCD的对角线AC、BD相交于点O,则下列说法一定正确的是( )
A、x=2 B、x=0 C、x=﹣1 D、x=﹣38. 如图,▱ABCD的对角线AC、BD相交于点O,则下列说法一定正确的是( )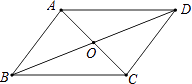 A、AO=OD B、AO⊥OD C、AO=OC D、AO⊥AB9. 如图,点A的坐标为(﹣2,0),点B在直线y=x上运动,当线段AB最短时,点B的坐标为( )
A、AO=OD B、AO⊥OD C、AO=OC D、AO⊥AB9. 如图,点A的坐标为(﹣2,0),点B在直线y=x上运动,当线段AB最短时,点B的坐标为( ) A、( , -) B、(- , -) C、(0,0) D、(﹣1,﹣1)10. 一列数a1 , a2 , a3 , …,其中a1= , an=(a为不小于2的整数),则a2014=( )A、 B、2 C、-1 D、-211.
A、( , -) B、(- , -) C、(0,0) D、(﹣1,﹣1)10. 一列数a1 , a2 , a3 , …,其中a1= , an=(a为不小于2的整数),则a2014=( )A、 B、2 C、-1 D、-211.如图,在△ABC中,点O是△ABC的内心,连接OB,OC,过点O作EF∥BC分别交AB,AC于点E,F.已知△ABC的周长为8,BC=x,△AEF的周长为y,则表示y与x的函数图象大致是( )
 A、
A、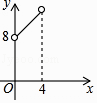 B、
B、 C、
C、 D、
D、
二、填空题
-
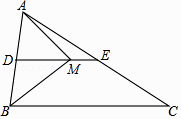
12. 计算: -6 =13. 已知 ,则 的取值范围是。14. 已知一组数据:3,5,4,5,2,5,4,则这组数据的中位数为.15. 在△ABC中,AB=6,点D是AB的中点,过点D作DE∥BC,交AC于点E,点M在DE上,且ME= DM.当AM⊥BM时,则BC的长为 .
 16.
16.如图所示,小明为了测量学校里一池塘的宽度AB,选取可以直达A、B两点的点O处,再分别取OA、OB的中点M、N,量得MN=20m,则池塘的宽度AB为 m.
 17. 如图,Rt△ABC中,BC=AC=2,D是斜边AB上一个动点,把△ACD沿直线CD折叠,点A落在同一平面内的A′处,当A′D平行于Rt△ABC的直角边时,AD的长为 .
17. 如图,Rt△ABC中,BC=AC=2,D是斜边AB上一个动点,把△ACD沿直线CD折叠,点A落在同一平面内的A′处,当A′D平行于Rt△ABC的直角边时,AD的长为 .
三、解答题
-
18. 先化简再求值:( +1)÷ ,其中a=2+ .19. 某校为了解学生每天参加户外活动的情况,随机抽查了100名学生每天参加户外活动的时间情况,并将抽查结果绘制成如图所示的扇形统计图.
请你根据图中提供的信息解答下列问题:
 (1)、请直接写出图a的值,并求出本次抽查中学生每天参加户外活动时间的中位数;(2)、求本次抽查中学生每天参加户外活动的平均时间.20. 如图,以BC为底边的等腰△ABC,点D,E,G分别在BC,AB,AC上,且EG∥BC,DE∥AC,延长GE至点F,使得BE=BF.
(1)、请直接写出图a的值,并求出本次抽查中学生每天参加户外活动时间的中位数;(2)、求本次抽查中学生每天参加户外活动的平均时间.20. 如图,以BC为底边的等腰△ABC,点D,E,G分别在BC,AB,AC上,且EG∥BC,DE∥AC,延长GE至点F,使得BE=BF.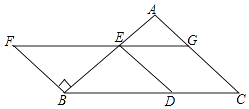 (1)、求证:四边形BDEF为平行四边形;
(1)、求证:四边形BDEF为平行四边形;
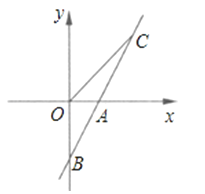
(2)、当∠C=45°,BD=2时,求D,F两点间的距离.21. 如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,﹣2).(1)求直线AB的解析式;
(2)若直线AB上的点C在第一象限,且S△BOC=2,求点C的坐标.
 22. 在一条笔直的公路上有A、B两地,甲骑自行车从A地到B地;乙骑自行车从B地到A地,到达A地后立即按原路返回,如图是甲、乙两人离B地的距离y(km)与行驶时x(h)之间的函数图象,根据图象解答以下问题:
22. 在一条笔直的公路上有A、B两地,甲骑自行车从A地到B地;乙骑自行车从B地到A地,到达A地后立即按原路返回,如图是甲、乙两人离B地的距离y(km)与行驶时x(h)之间的函数图象,根据图象解答以下问题: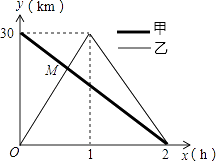 (1)、写出A、B两地之间的距离;(2)、求出点M的坐标,并解释该点坐标所表示的实际意义;(3)、若两人之间保持的距离不超过3km时,能够用无线对讲机保持联系,请直接写出甲、乙两人能够用无线对讲机保持联系时x的取值范围.23.
(1)、写出A、B两地之间的距离;(2)、求出点M的坐标,并解释该点坐标所表示的实际意义;(3)、若两人之间保持的距离不超过3km时,能够用无线对讲机保持联系,请直接写出甲、乙两人能够用无线对讲机保持联系时x的取值范围.23.一张矩形纸片,剪下一个正方形,剩下一个矩形,称为第一次操作;在剩下的矩形纸片中再剪下一个正方形,剩下一个矩形,称为第二次操作…若在第 n 次操作后,剩下的矩形为正方形,则称原矩形为n阶奇异矩形.如图1,矩形ABCD中,若AB=2,BC=6,则称矩形ABCD为2阶奇异矩形.
 (1)、
(1)、判断与操作:
如图2,矩形ABCD的长为5,宽为2,它是奇异矩形吗?
如果是,请写出它是几阶奇异矩形,并在图中画出裁剪线;如果不是,请说明理由.
 (2)、探究与计算:
(2)、探究与计算:已知矩形ABCD的一边长为20,另一边长为a(a<20),且它是3阶奇异矩形,请画出矩形ABCD及裁剪线的示意图,并在图的下方写出a的值.
24. 已知两个共一个顶点的等腰Rt△ABC,Rt△CEF,∠ABC=∠CEF=90°,连接AF,M是AF的中点,连接MB、ME. (1)、如图,当CB与CE在同一直线上时,求证:MB∥CF;(2)、如图,若CB=a,CE=2a,求BM,ME的长;25. 某工厂在生产过程中每消耗1万度电可以产生产值5.5万元,电力公司规定,该工厂每月用电量不得超过16万度,月用电量不超过4万度时,单价是1万元/万度;超过4万度时,超过部分电量单价将按用电量进行调查,电价y与月用电量x的函数关系可用如图来表示.(效益=产值﹣用电量×电价)
(1)、如图,当CB与CE在同一直线上时,求证:MB∥CF;(2)、如图,若CB=a,CE=2a,求BM,ME的长;25. 某工厂在生产过程中每消耗1万度电可以产生产值5.5万元,电力公司规定,该工厂每月用电量不得超过16万度,月用电量不超过4万度时,单价是1万元/万度;超过4万度时,超过部分电量单价将按用电量进行调查,电价y与月用电量x的函数关系可用如图来表示.(效益=产值﹣用电量×电价) (1)、设工厂的月效益为z(万元),写出z与月用电量x(万度)之间的函数关系式,并写出自变量的取值范围;(2)、求工厂最大月效益.
(1)、设工厂的月效益为z(万元),写出z与月用电量x(万度)之间的函数关系式,并写出自变量的取值范围;(2)、求工厂最大月效益.