2017-2018学年人教版八年级下学期数学期末模拟试卷(1)
试卷更新日期:2018-06-14 类型:期末考试
一、选择题
-
1. 在函数 中,自变量x的取值范围是( )A、x≥﹣1 B、x>﹣1且x≠ C、x≥﹣1且x≠ D、x>﹣12. 某校调查了20名男生某一周参加篮球运动的次数,调查结果如表所示,那么这20名男生该周参加篮球运动次数的平均数是( )
次数
2
3
4
5
人数
2
2
10
6
A、3次 B、3.5次 C、4次 D、4.5次3. 函数y= 中自变量x的取值范围在数轴上表示正确的是( )A、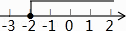 B、
B、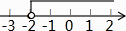 C、
C、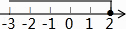 D、
D、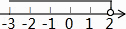 4. 如图,把正方形纸片ABCD沿对边中点所在的直线对折后展开,折痕为MN,再过点B折叠纸片,使点A落在MN上的点F处,折痕为BE.若AB的长为2,则FM的长为( )
4. 如图,把正方形纸片ABCD沿对边中点所在的直线对折后展开,折痕为MN,再过点B折叠纸片,使点A落在MN上的点F处,折痕为BE.若AB的长为2,则FM的长为( )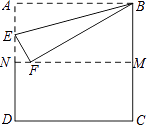 A、2 B、 C、 D、15. 根据PM2.5空气质量标准:24小时PM2.5均值在1~35(微克/立方米)的空气质量等级为优.将环保部门对我市PM2.5一周的检测数据制作成如下统计表.这组PM2.5数据的中位数是( )
A、2 B、 C、 D、15. 根据PM2.5空气质量标准:24小时PM2.5均值在1~35(微克/立方米)的空气质量等级为优.将环保部门对我市PM2.5一周的检测数据制作成如下统计表.这组PM2.5数据的中位数是( )天数
3
1
1
1
1
PM2.5
18
20
21
29
30
A、21微克/立方米 B、20微克/立方米 C、19微克/立方米 D、18微克/立方米6. 下列各式变形中,正确的是( )A、x2•x3=x6 B、 =|x| C、(x2﹣ )÷x=x﹣1 D、x2﹣x+1=(x﹣ )2+7. 如图,函数y1=﹣2x与y2=ax+3的图象相交于点A(m,2),则关于x的不等式﹣2x>ax+3的解集是( )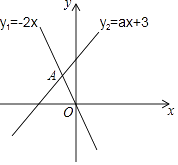 A、x>2 B、x<2 C、x>﹣1 D、x<﹣18. 如图,矩形ABCD的对角线AC与BD交于点O,过点O作BD的垂线分别交AD,BC于E,F两点.若AC=2 ,∠AEO=120°,则FC的长度为( )
A、x>2 B、x<2 C、x>﹣1 D、x<﹣18. 如图,矩形ABCD的对角线AC与BD交于点O,过点O作BD的垂线分别交AD,BC于E,F两点.若AC=2 ,∠AEO=120°,则FC的长度为( ) A、1 B、2 C、 D、9.
A、1 B、2 C、 D、9.梅凯种子公司以一定价格销售“黄金1号”玉米种子,如果一次购买10千克以上(不含10千克)的种子,超过10千克的那部分种子的价格将打折,并依此得到付款金额y(单位:元)与一次购买种子数量x(单位:千克)之间的函数关系如图所示.下列四种说法:
①一次购买种子数量不超过10千克时,销售价格为5元/千克;
②一次购买30千克种子时,付款金额为100元;
③一次购买10千克以上种子时,超过10千克的那部分种子的价格打五折:
④一次购买40千克种子比分两次购买且每次购买20千克种子少花25元钱.
其中正确的个数是( ).
 A、1个 B、2个 C、3个 D、4个10. 如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,点E是AB的中点,CD=DE=a,则AB的长为( )
A、1个 B、2个 C、3个 D、4个10. 如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,点E是AB的中点,CD=DE=a,则AB的长为( )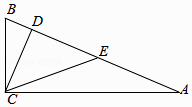 A、2a B、2 a C、3a D、11.
A、2a B、2 a C、3a D、11.在每个小正方形的边长为 的网格图形中,每个小正方形的顶点称为格点.从一个格点移动到与之相距 的另一个格点的运动称为一次跳马变换.例如,在 的正方形网格图形中(如图1),从点 经过一次跳马变换可以到达点 , , , 等处.现有 的正方形网格图形(如图2),则从该正方形的顶点 经过跳马变换到达与其相对的顶点 ,最少需要跳马变换的次数是( )
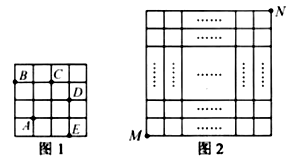 A、 B、 C、 D、12.
A、 B、 C、 D、12.如图,在▱ABCD中,∠DAB的平分线交CD于点E,交BC的延长线于点G,∠ABC的平分线交CD于点F,交AD的延长线于点H,AG与BH交于点O,连接BE,下列结论错误的是( )
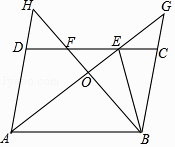 A、BO=OH B、DF=CE C、DH=CG D、AB=AE
A、BO=OH B、DF=CE C、DH=CG D、AB=AE二、填空题
-
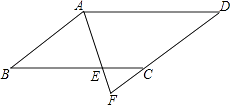
13. 计算: = .14. 如图,E是▱ABCD边BC上一点,且AB=BE,连结AE,并延长AE与DC的延长线交于点F,∠F=70°,则∠D=度.
 15.
15.七(1)班举行投篮比赛,每人投5球.如图是全班学生投进球数的扇形统计图,则投进球数的众数是 .
 16. 已知方程组的解为 , 则一次函数y=﹣x+1和y=2x﹣2的图象的交点坐标为 .17. 有一面积为5 的等腰三角形,它的一个内角是30°,则以它的腰长为边的正方形的面积为 .18. 如图,在平面直角坐标系中,等腰直角三角形OA1A2的直角边OA1在y轴的正半轴上,且OA1=A1A2=1,以OA2为直角边作第二个等腰直角三角形OA2A3 , 以OA3为直角边作第三个等腰直角三角形OA3A4 , …,依此规律,得到等腰直角三角形OA2017A2018 , 则点A2017的坐标为 .
16. 已知方程组的解为 , 则一次函数y=﹣x+1和y=2x﹣2的图象的交点坐标为 .17. 有一面积为5 的等腰三角形,它的一个内角是30°,则以它的腰长为边的正方形的面积为 .18. 如图,在平面直角坐标系中,等腰直角三角形OA1A2的直角边OA1在y轴的正半轴上,且OA1=A1A2=1,以OA2为直角边作第二个等腰直角三角形OA2A3 , 以OA3为直角边作第三个等腰直角三角形OA3A4 , …,依此规律,得到等腰直角三角形OA2017A2018 , 则点A2017的坐标为 .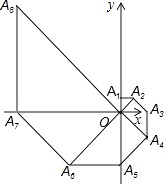
三、综合题
-
19. 计算: + -( )-1-(2017+ )0.20. 已知y是x的一次函数,当x=3时,y=1;当x=﹣2时,y=﹣4,求这个一次函数的解析式.21. 某工厂甲、乙两个部门各有员工400人,为了解这两个部门员工的生产技能情况,进行了抽样调查,过程如下,请补充完整.
收集数据
从甲、乙两个部门各随机抽取20名员工,进行了生产技能测试,测试成绩(百分制)如下:
甲 78 86 74 81 75 76 87 70 75 90 75 79 81 70 74 80 86 69 83 77
乙 93 73 88 81 72 81 94 83 77 83 80 81 70 81 73 78 82 80 70 40
整理、描述数据
按如下分数段整理、描述这两组样本数据:
成绩x
人数
部门
40≤x≤49
50≤x≤59
60≤x≤69
70≤x≤79
80≤x≤89
90≤x≤100
甲
0
0
1
11
7
1
乙
(说明:成绩80分及以上为生产技能优秀,70﹣﹣79分为生产技能良好,60﹣﹣69分为生产技能合格,60分以下为生产技能不合格)
分析数据
两组样本数据的平均数、中位数、众数如下表所示:
部门
平均数
中位数
众数
甲
78.3
77.5
75
乙
78
80.5
81
得出结论:a.估计乙部门生产技能优秀的员工人数为;b.可以推断出部门员工的生产技能水平较高,理由为 . (至少从两个不同的角度说明推断的合理性)
22. 如图,四边形ABCD是正方形,E、F分别是了AB、AD上的一点,且BF⊥CE,垂足为G,求证:AF=BE.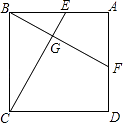 23. 下表是世界人口增长趋势数据表:
23. 下表是世界人口增长趋势数据表:年份x
1960
1974
1987
1999
2010
人口数量y(亿)
30
40
50
60
69
(1)、请你认真研究上面数据表,求出从1960年到2010年世界人口平均每年增长多少亿人;(2)、利用你在(1)中所得到的结论,以1960年30亿人口为基础,设计一个最能反映人口数量y关于年份x的函数关系式,并求出这个函数的解析式;(3)、利用你在(2)中所得的函数解析式,预测2020年世界人口将达到多少亿人.24. 为养成学生课外阅读的习惯,各学校普遍开展了“我的梦 中国梦”课外阅读活动,某校为了解七年级1200名学生课外日阅读所用时间情况,从中随机抽查了部分同学,进行了相关统计,整理并绘制出如下不完整的频数分布表和频数分布直方图,请根据图表信息解答下列问题:组别
时间段(小时)
频数
频率
1
0≤x<0.5
10
0.05
2
0.5≤x<1.0
20
0.10
3
1.0≤x<1.5
80
b
4
1.5≤x<2.0
a
0.35
5
2.0≤x<2.5
12
0.06
6
2.5≤x<3.0
8
0.04
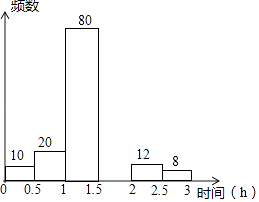 (1)、表中a= , b=;(2)、请补全频数分布直方图中空缺的部分;(3)、样本中,学生日阅读所用时间的中位数落在第组;(4)、请估计该校七年级学生日阅读量不足1小时的人数.25.
(1)、表中a= , b=;(2)、请补全频数分布直方图中空缺的部分;(3)、样本中,学生日阅读所用时间的中位数落在第组;(4)、请估计该校七年级学生日阅读量不足1小时的人数.25.如图1,在△ABC和△EDC中,AC=CE=CB=CD;∠ACB=∠DCE=90°,AB与CE交于F,ED与AB,BC,分别交于M,H.
 (1)、求证:CF=CH;(2)、如图2,△ABC不动,将△EDC绕点C旋转到∠BCE=45°时,试判断四边形ACDM是什么四边形?并证明你的结论.26. 【问题探究】
(1)、求证:CF=CH;(2)、如图2,△ABC不动,将△EDC绕点C旋转到∠BCE=45°时,试判断四边形ACDM是什么四边形?并证明你的结论.26. 【问题探究】(1)如图1,锐角△ABC中分别以AB、AC为边向外作等腰△ABE和等腰△ACD,使AE=AB,AD=AC,∠BAE=∠CAD,连接BD,CE,试猜想BD与CE的大小关系,并说明理由.
【深入探究】
(2)如图2,四边形ABCD中,AB=7cm,BC=3cm,∠ABC=∠ACD=∠ADC=45°,求BD的长.
(3)如图3,在(2)的条件下,当△ACD在线段AC的左侧时,求BD的长.
