2017-2018学年浙教版七年级下学期数学期末模拟试卷（3）

试卷更新日期：2018-06-14 类型：期末考试

进入出卷网下载

一、选择题

1. 下列计算正确的是（）

A、(－x²)³ ＝x⁵ B、x⁸ ÷x⁴ ＝x² C、x³ ＋3x³ ＝3x⁶ D、(－x²)³ ＝－x⁶

查看试题解析
2. 下列各式从左到右的变形中，是因式分解的为（）

A、x（a﹣b）=ax﹣bx B、x²﹣1+y²=（x﹣1）（x+1）+y² C、x²﹣1=（x+1）（x﹣1） D、ax+bx+c=x（a+b）+c

查看试题解析
3. 已知ΔABC中，∠A∶∠B∶∠C=3∶7∶8，则ΔABC的形状是（）

A、钝角三角形 B、直角三角形 C、锐角三角形 D、都有可能

查看试题解析
4. 当x＝3时，下列各式中值为零的分式是（）

A、 $\frac{x - 3}{x^{2} - 6 x + 9}$ B、 $\frac{2}{x - 3}$ C、 $\frac{3 x - 9}{x^{2} + 9}$ D、 $\frac{3 - x}{2 x - 6}$

查看试题解析
5. 在多项式x²+9中添加一个单项式，使其成为一个完全平方式，则添加的单项式可以是（　　）

A、x B、3x C、6x D、9x

查看试题解析
6.
如图，已知a∥b，∠1=65°，则∠2的度数为（　　）

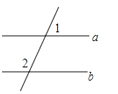A、65° B、125° C、115° D、25°

查看试题解析
7. 绿化队原来用浸灌方式浇绿地，a天用水m吨，现在改用喷灌方式，可使这些水多用3天，那么现在比原来每天节约用水的吨数为（）

A、 $\frac{3 a}{m}$ B、 $\frac{a m}{a + 3}$ C、 $\frac{3 m}{a}$ D、 $\frac{3 m}{a (a + 3)}$

查看试题解析
8. 多项式（x+2）（2x﹣1）﹣2（x+2）可以因式分解成（x+m）（2x+n），则m﹣n的值是（）

A、2 B、﹣2 C、4 D、5

查看试题解析
9. 如图，AB∥EF∥CD，EG∥DB，则图中与∠1相等的角（∠1除外）共有（）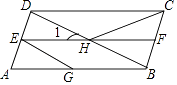

A、6个 B、5个 C、4个 D、3个

查看试题解析
10. 若4x²﹣2（k﹣1）x+9是完全平方式，则k的值为（）

A、±2 B、±5 C、7或﹣5 D、﹣7或5

查看试题解析

二、填空题

11. 若方程组 $\{\begin{matrix} 3 x - 5 y = 2 a \\ 2 x + 7 y = a - 18 \end{matrix}$ 的解x、y互为相反数，则a= ．

查看试题解析
12. 简便计算： ${(- \frac{1}{3})}^{100} \times 27^{33}$ = ．

查看试题解析
13. 如表是某校八年级（8）班共50位同学身高情况的频数分布表，则表中的组距是，身高最大值与最小值的差至多是cm．
组别（cm）
145.5～152．.5
152.5～159.5
159.5～166.5
166.5～173.5
频数（人）
9
19
14
8

查看试题解析
14. 已知分式 $\frac{x - 3}{x^{2} - 5 x + a}$ ，当x=2时，分式无意义，则a=；当a为a＜6的一个整数时，使分式无意义的x的值共有个．

查看试题解析
15. 在日常生活中如取款、上网等都需要密码．有一种用“因式分解”法产生的密码，方便记忆．原理是：如对于多项式x⁴﹣y⁴ ，因式分解的结果是（x﹣y）（x+y）（x²+y²），若取x=9，y=9时，则各个因式的值是：（x﹣y）=0，（x+y）=18，（x²+y²）=162，于是就可以把“018162”作为一个六位数的密码．对于多项式4x³﹣xy² ，取x=10，y=10时，用上述方法产生的密码是：（写出一个即可）．

查看试题解析
16.
观察下列图形：已知a∥b，在第一个图中，可得∠1+∠2=180°，则按照以上规律，∠1+∠2+∠P₁+…+∠P_n=度．

查看试题解析

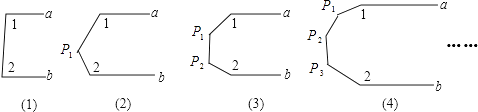
三、综合题

17. 计算：

(1)、（-2xy2）²÷ $\frac{1}{3}$ xy

(2)、（x+2）²+2（x+2）（x-4）-（x+3）（x-3）

查看试题解析
18. 计算

(1)、计算： $\frac{a - 1}{a} \div \frac{a^{2} - 1}{a^{2} + 2 a}$

(2)、解方程： $\frac{x}{2 x - 1} = 2 - \frac{3}{1 - 2 x}$ ．

查看试题解析
19. 商场经营的某品牌童装，4月的销售额为20000元，为扩大销量，5月份商场对这种童装打9折销售，结果销量增加了50件，销售额增加了7000元．

(1)、求该童装4月份的销售单价；

(2)、若4月份销售这种童装获利8000元，6月全月商场进行“六一儿童节”促销活动．童装在4月售价的基础上一律打8折销售，若该童装的成本不变，则销量至少为多少件，才能保证6月的利润比4月的利润至少增长25%？

查看试题解析
20. 综合题

(1)、如图a示，AB∥CD，且点E在射线AB与CD之间，请说明∠AEC=∠A+∠C的理由．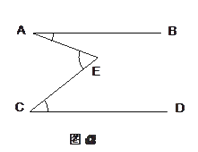

(2)、现在如图b示，仍有AB∥CD，但点E在AB与CD的上方，①请尝试探索∠1，∠2，∠E三者的数量关系. ②请说明理由.

查看试题解析
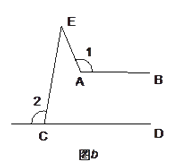21. 某中学组织全体学生参加了“服务社会献爱心”的活动，为了了解九年级学生参加活动情况，从九年级学生中随机抽取部分学生进行调查，统计了该天他们打扫街道，去敬老院服务和到社区文艺演出的人数，并绘制了如下不完整的条形统计图和扇形统计图，其中到社区文艺演出的人数占所调查的九年级学生人数的 $\frac{3}{10}$ ，请根据两幅统计图中的信息，回答下列问题：

(1)、本次调查共抽取了多少名九年级学生？

(2)、补全条形统计图．

(3)、若该中学九年级共有1400名学生，请你估计该中学九年级去敬老院的学生有多少名？

查看试题解析
22. 某工厂承接了一批纸箱加工任务，用如图1所示的长方形和正方形纸板（长方形的宽与正方形的边长相等）加工成如图所示的竖式与横式两种无盖的长方形纸箱．（加工时接缝材料不计）

(1)、若该厂购进正方形纸板1000张，长方形纸板2000张．问竖式纸盒，横式纸盒各加工多少个，恰好能将购进的纸板全部用完；

(2)、该工厂某一天使用的材料清单上显示，这天一共使用正方形纸板50张，长方形纸板a张，全部加工成上述两种纸盒，且120＜a＜136，试求在这一天加工两种纸盒时，a的所有可能值．

查看试题解析

组别（cm）	145.5～152．.5	152.5～159.5	159.5～166.5	166.5～173.5
频数（人）	9	19	14	8