浙江省泉山市台商投资区2016-2017学年八年级下学期数学期末考试试卷
试卷更新日期:2018-06-13 类型:期末考试
一、单选题
-
1. 要使分式 有意义, 必须满足的条件是( ).
A、 B、 C、 D、2. 在平面直角坐标系中,点( , )关于 轴对称的点的坐标是( )
A、( , ) B、( , ) C、( , ) D、( , )3. 在某次数学测验中,某小组8名同学的成绩如下:81,73,81,81,85,83,87,89,则这组数据的中位数、众数分别为( ).A、80,81 B、81,89 C、82,81 D、73,814. 已知反比例函数 ,在下列结论中,不正确的是( ).A、图象必经过点(1,2); B、图象在第一、三象限; C、 随 的增大而减少; D、若 >1,则 <2 。5. 如图所示,将一张矩形纸片对折两次后剪下一个角,然后打开.如果要剪出一个正方形,那么剪口线与折痕所成的锐角大小是( )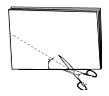 A、 B、 C、 D、6. 已知菱形ABCD的对角线AC,BD的长分别为6和8,则该菱形面积是( )A、14; B、24; C、30; D、48.7. 如图,点P是 轴正半轴上的一个动点,过点P作PQ⊥ 轴交双曲线 (x>0)于点Q,连结OQ. 当点P沿 轴的正方向运动时,Rt△QOP的面积( ).
A、 B、 C、 D、6. 已知菱形ABCD的对角线AC,BD的长分别为6和8,则该菱形面积是( )A、14; B、24; C、30; D、48.7. 如图,点P是 轴正半轴上的一个动点,过点P作PQ⊥ 轴交双曲线 (x>0)于点Q,连结OQ. 当点P沿 轴的正方向运动时,Rt△QOP的面积( ).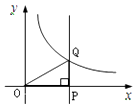 A、保持不变 B、逐渐减小 C、逐渐增大 D、无法确定8. 如图,函数 ( )和 ( )的图象相交于点A ,则不等式 > 的解集为( )
A、保持不变 B、逐渐减小 C、逐渐增大 D、无法确定8. 如图,函数 ( )和 ( )的图象相交于点A ,则不等式 > 的解集为( )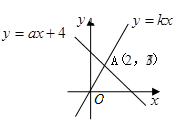 A、 > B、 <
A、 > B、 < C、 >
D、 <
9. 如图,已知四边形 是平行四边形,则下列结论中正确的是( ).
C、 >
D、 <
9. 如图,已知四边形 是平行四边形,则下列结论中正确的是( ).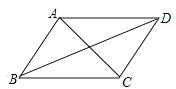 A、当 时,它是矩形 B、当 时,它是正方形 C、当 时,它是菱形 D、当 时,它是菱形10. 如图,已知在正方形 中,点 分别在 上,△ 是等边三角形,连接 交 于 ,给出下列结论:
A、当 时,它是矩形 B、当 时,它是正方形 C、当 时,它是菱形 D、当 时,它是菱形10. 如图,已知在正方形 中,点 分别在 上,△ 是等边三角形,连接 交 于 ,给出下列结论: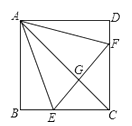
① ; ② ;
③ 垂直平分 ; ④ .
其中结论正确的共有( ).
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 在▱ABCD中,∠A = ,则∠C= .12. 人体中红细胞的直径大约为0.000 007 7米,则数据0.000 007 7用科学记数法表示为 .13. 将直线y=3x向上平移1个单位,可以得到直线 .
14. 在函数y= (m -3)x -2(m是常数)中, y随着x的增大而增大,则m的取值范围是。
15. 如图,已知AD∥BC,要使四边形ABCD为平行四边形,需要增加的一个条是: . (只填一个你认为正确的条件即可,不添加任何线段与字母)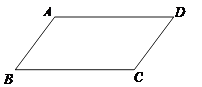 16. 如图,已知:在▱ABCD中,AB=AD=2,∠DAB=60°,F为AC上一点,E为AB中点.
16. 如图,已知:在▱ABCD中,AB=AD=2,∠DAB=60°,F为AC上一点,E为AB中点.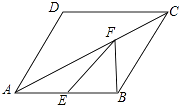
▱ABCD的周长是;
EF+BF的最小值为 .
三、解答题
-
17. 计算: .18. 先化简,再求值: ,其中 .19. 解方程:20. 为了从甲、乙两人中选拔一人参加射击比赛,现对他们的射击成绩进行了测试,5次打靶命中的环数如右:甲:8,7,10,7,8; 乙:9,5,10,9,7.(1)、将下表填写完整:
平 均 数
方 差
甲
乙
3.2
(2)、若你是教练,根据以上信息,你会选择谁参加射击比赛,理由是什么?21. 已知:如图,在▱ABCD中,E、F是对角线AC上的两点,且AE=CF.求证:四边形BFDE是平行四边形.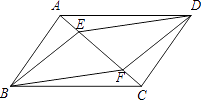 22. 如图,在平面直角坐标系 中,直线 与 轴交于点 ,与双曲线 在第二象限内交于点 (-3, ).
22. 如图,在平面直角坐标系 中,直线 与 轴交于点 ,与双曲线 在第二象限内交于点 (-3, ).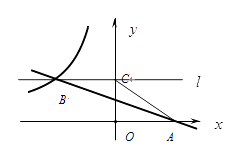 (1)、求 和 的值;(2)、过点 作直线 平行 轴交 轴于点 ,连结AC,求△ 的面积.
(1)、求 和 的值;(2)、过点 作直线 平行 轴交 轴于点 ,连结AC,求△ 的面积.
23. 甲、乙两辆汽车同时分别从A、B两城沿同一条高速公路匀速驶向C城.已知A、C两城的距离为360km,B、C两城的距离为320km,甲车比乙车的速度快10km/h,结果两辆车同时到达C城.设乙车的速度为x km/h.(1)、根据题意填写下表:行驶的路程(km)
速度(km/h)
所需时间(h)
甲车
360
乙车
320
x
(2)、求甲、乙两车的速度.24. 如图,直线 与 轴、 轴分别相交于点A和B.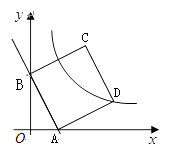 (1)、直接写出坐标:点A , 点B;(2)、以线段AB为一边在第一象限内作□ABCD,其顶点D( , )在双曲线 ( > )上.
(1)、直接写出坐标:点A , 点B;(2)、以线段AB为一边在第一象限内作□ABCD,其顶点D( , )在双曲线 ( > )上.①求证:四边形ABCD是正方形;
②试探索:将正方形ABCD沿 轴向左平移多少个单位长度时,点C恰好落在双曲线 ( > )上.
25. 如图,正方形 的边 、 在坐标轴上,点 坐标为 ,将正方形 绕点 逆时针旋转角度 ,得到正方形 , 交线段 于点 , 的延长线交线段 于点 ,连结 、 .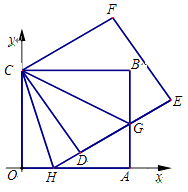 (1)、求证: 平分 ;
(1)、求证: 平分 ;
(2)、在正方形 绕点 逆时针旋转的过程中,求线段 、 、 之间的数量关系;
(3)、连结 、 、 、 ,在旋转的过程中,四边形 是否能在点G满足一定的条件下成为矩形?若能,试求出直线 的解析式;若不能,请说明理由.