广西钦州市钦州港经济技术开发区2016-2017学年八年级下学期数学期末考试试卷
试卷更新日期:2018-06-13 类型:期末考试
一、单选题
-
1. 下列各组数中以a,b,c为边的三角形不是直角三角形的是( )A、a=2,b=3,c=4 B、a=7,b=24,c=25 C、a=6,b=8,c=10 D、a=3,b=4,c=52. 下列各组数中,能构成直角三角形的是( )A、4,5,6 B、1,1, C、6,8,11 D、5,12,233. △ABC的三边长分别为a,b,c,下列条件:①∠A=∠B-∠C;②∠A:∠B:∠C=3:4:5;③a2=(b+c)(b-c);④a:b:c=5:12:13,其中能判断△ABC是直角三角形的个数有( )A、1个 B、2个 C、3个 D、4个4. 今年以来,某种食品不断上涨,在9月份的售价为8.1元/kg,11月份的售价为10元/kg。这种食品平均每月上涨的百分率约等于( )
A、15% B、11% C、20% D、9%5. 下列命题的逆命题不正确的是( )
A、同旁内角互补,两直线平行 B、正方形的四个角都是直角 C、若xy=0,则x=0 D、平行四边形的对角线互相平分6. 下列说法中的错误的是( )A、一组邻边相等的矩形是正方形 B、一组邻边相等的平行四边形是菱形 C、一组对边相等且有一个角是直角的四边形是矩形 D、一组对边平行且相等的四边形是平行四边形7. 矩形的两边长分别是3和5,则它的对角线长是( )A、4 B、6 C、 D、78. 若在同一直角坐标系中,作 , , 的图像,则它们( )A、都关于 轴对称 B、开口方向相同 C、都经过原点 D、互相可以通过平移得到9. 已知点A为某封闭图形边界上一定点,动点P从点A出发,沿其边界顺时针匀速运动一周.设点P运动的时间为x,线段AP的长为y.表示y与x的函数关系的图象大致如右图所示,则该封闭图形可能是 ( )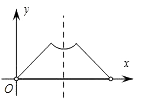 A、
A、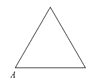 B、
B、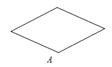 C、
C、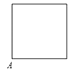 D、
D、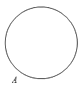 10. 等腰三角形的周长是40cm,腰长y (cm)是底边长x (cm)的函数解析式正确的是( )
10. 等腰三角形的周长是40cm,腰长y (cm)是底边长x (cm)的函数解析式正确的是( )
A、y=-0.5x+20 ( 0<x<20) B、y=-0.5x+20 (10<x<20) C、y=-2x+40 (10<x<20) D、y=-2x+40 (0<x<20)11. 如果线段AB=5cm,BC=4cm,且A,B,C在同一条直线上,那么A,C两点间的距离是( )
A、1cm B、9cm C、1cm或9cm D、以上答案都不正确12. 菱形具有而矩形不具有的性质是( )
A、对角相等 B、四边相等 C、对角线互相平分 D、四角相等13. 一个三角形的三边的长分别是3、4、5,则这个三角形最长边上的高是( )
A、4 B、 C、 D、二、填空题
-
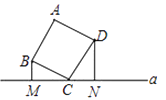
14. 如图,正方形ABCD的顶点C在直线a上,且点B,D到a的距离分别是1,2.则 这个正方 形的边长是 。
 15. 在女子3000米的长跑中,运动员的平均速度v= ,则这个关系式中自变量是 .16. 函数y= 的定义域是 .
15. 在女子3000米的长跑中,运动员的平均速度v= ,则这个关系式中自变量是 .16. 函数y= 的定义域是 .
17. 如图,△ABC中,M是BC中点,AD平分∠BAC,BD⊥AD于D,若AB=12,AC=16,则MD等于 .
三、解答题
-
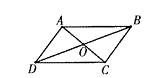
18. 如图,在▱ABCD中,E、F分别为边AB、CD的中点,连接DE、BF、BD.
 (1)、求证:△ADE≌△CBF;(2)、当AD⊥BD时,请你判断四边形BFDE的形状,并说明理由.
(1)、求证:△ADE≌△CBF;(2)、当AD⊥BD时,请你判断四边形BFDE的形状,并说明理由.
19. 在△ABC中,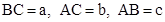 ,设c为最长边.当
,设c为最长边.当  时,△ABC是直角三角形;当
时,△ABC是直角三角形;当  时,利用代数式
时,利用代数式  和
和  的大小关系,可以判断△ABC的形状(按角分类). (1)、请你通过画图探究并判断:当△ABC三边长分别为6,8,9时,△ABC为三角形;当△ABC三边长分别为6,8,11时,△ABC为三角形.(2)、小明同学根据上述探究,有下面的猜想:“当 时,△ABC为锐角三角形;当 时,△ABC为钝角三角形.”请你根据小明的猜想完成下面的问题:
的大小关系,可以判断△ABC的形状(按角分类). (1)、请你通过画图探究并判断:当△ABC三边长分别为6,8,9时,△ABC为三角形;当△ABC三边长分别为6,8,11时,△ABC为三角形.(2)、小明同学根据上述探究,有下面的猜想:“当 时,△ABC为锐角三角形;当 时,△ABC为钝角三角形.”请你根据小明的猜想完成下面的问题:当 , 时,最长边c在什么范围内取值时,△ABC是直角三角形、锐角三角形、钝角三角形?