福建省福清市2016-2017学年八年级下学期数学期末考试试卷
试卷更新日期:2018-06-13 类型:期末考试
一、单选题
-
1. 已知函数 在实数范围内有意义,则自变量x的取值范围是( )
A、 B、 C、 D、2. 下列式子中,表示y是x的正比例函数是( )A、 B、 C、 D、3. 下列二次根式中不能够与 合并的是( )A、 B、 C、 D、4. 学校升旗仪式上,徐徐上升的国旗的高度与时间的关系可以用一幅图近似地刻画,这幅图是下图中的( )A、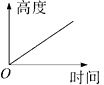 B、
B、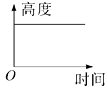 C、
C、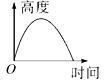 D、
D、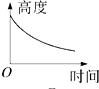 5. 期中考试后,班里有两位同学议论他们所在小组同学的数学成绩,甲说:“我们组成绩是88分的同学最多”,乙说:“我们组的11位同学成绩排在最中间的恰好也是88分”,上面两位同学的话能反映处的统计量分别是( )A、众数和平均数 B、平均数和中位数 C、众数和方差 D、众数和中位数6. 满足下列条件的△ABC不是直角三角形的是( )A、BC=1,AC=2,AB= B、BC:AC:AB=3:4:5 C、∠A+∠B=∠C D、∠A:∠B:∠C=3:4:57. 如图,已知四边形ABCD是平行四边形,下列结论中错误的是( )
5. 期中考试后,班里有两位同学议论他们所在小组同学的数学成绩,甲说:“我们组成绩是88分的同学最多”,乙说:“我们组的11位同学成绩排在最中间的恰好也是88分”,上面两位同学的话能反映处的统计量分别是( )A、众数和平均数 B、平均数和中位数 C、众数和方差 D、众数和中位数6. 满足下列条件的△ABC不是直角三角形的是( )A、BC=1,AC=2,AB= B、BC:AC:AB=3:4:5 C、∠A+∠B=∠C D、∠A:∠B:∠C=3:4:57. 如图,已知四边形ABCD是平行四边形,下列结论中错误的是( )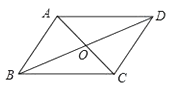 A、当AB=BC时,它是菱形 B、当AC⊥BD时,它是菱形 C、当AC=BD时,它是矩形 D、当∠ABC=90°时,它是正方形8. 如图,△ABC的中线BD、CE交于点O,连接OA,点G,F分别为OC,OB的中点,BC=4,AO=3,则四边形DEFG的周长为( )
A、当AB=BC时,它是菱形 B、当AC⊥BD时,它是菱形 C、当AC=BD时,它是矩形 D、当∠ABC=90°时,它是正方形8. 如图,△ABC的中线BD、CE交于点O,连接OA,点G,F分别为OC,OB的中点,BC=4,AO=3,则四边形DEFG的周长为( )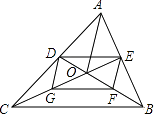 A、6 B、7 C、8 D、129. 在平面直角坐标系中,A(1,3),B(2,4),C(3,5),D(4,6)其中不与E(2,-3)在同一个函数图象上的一个点是( )A、点A B、点B C、点C D、点D10. 如图,点A,D分别在两条直线y=3x和y=x上,AD//x轴,已知B,C都在x轴上,且四边形ABCD是矩形,则 的值是( )
A、6 B、7 C、8 D、129. 在平面直角坐标系中,A(1,3),B(2,4),C(3,5),D(4,6)其中不与E(2,-3)在同一个函数图象上的一个点是( )A、点A B、点B C、点C D、点D10. 如图,点A,D分别在两条直线y=3x和y=x上,AD//x轴,已知B,C都在x轴上,且四边形ABCD是矩形,则 的值是( )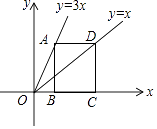 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 计算: =12. 已知函数y=kx-2,请你补充一个条件 , 使y随x的增大而减小。13. 设甲组数据:3,3,3,3的方差为 ,乙组数据:1,2,3的方差为 ,则 与 的大小关系是14. 已知点A(5,4),B(1,1),则线段AB的长
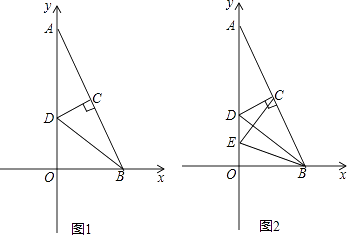
15. 如图,O是矩形ABCD的对角线AC的中点,M是AD的中点.若AB=5,AD=12,则四边形ABOM的周长为 .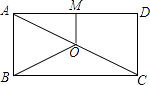 16. 如图,在平行四边形ABCD中,△ABD是等边三角形,BD=10,且两个顶点B、D分别在x轴,y轴上滑动,连接OC,则OC的最小值是。
16. 如图,在平行四边形ABCD中,△ABD是等边三角形,BD=10,且两个顶点B、D分别在x轴,y轴上滑动,连接OC,则OC的最小值是。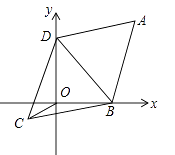
三、解答题
-
17. 计算:18. 求值:已知 , ,求 的值;
19. 如图,在△ABC中 , ,AC=6,求AB、BC的长。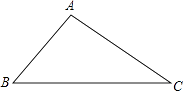 20. 已知一次函数 ,回答下列问题:(1)、若一次函数的图象过原点,求k的值;
20. 已知一次函数 ,回答下列问题:(1)、若一次函数的图象过原点,求k的值;
(2)、无论k取何值,该函数的图象总经过一个定点,请你求出这个定点的坐标。21. 如图,四边形ABCD是平行四边形,E是BC边上一点,只用一把无刻度的直尺在AD边上作点F,使得DF=BE. (1)、作出满足题意的点F,简要说明你的作图过程;(2)、依据你的作图,证明:DF=BE.22. 为宣传节约用水,小明随机调查了某小区部分家庭5月份的用水情况,并将收集的数据整理成如下统计图.
(1)、作出满足题意的点F,简要说明你的作图过程;(2)、依据你的作图,证明:DF=BE.22. 为宣传节约用水,小明随机调查了某小区部分家庭5月份的用水情况,并将收集的数据整理成如下统计图. (1)、小明一共调查了户家庭;所调查家庭5 月份用水量的众数是;
(1)、小明一共调查了户家庭;所调查家庭5 月份用水量的众数是;
(2)、求所调查家庭5 月份用水量的平均数;(3)、若该小区有400 户居民,请你估计这个小区5 月份的用水量.23. 如图,A、B两地相距600km,一辆动车从A地开往B地,一辆高铁从B地开往A地,高铁先出发,一小时后,动车才出发,设动车离A地的距离为y2(km),高铁离A地的距离为y1(km)高铁出发时间为t(h),变量y2和y1之间的关系图像如图所示: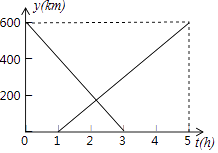 (1)、根据图像,高铁和动车的速度分别是;(2)、高铁出发多少小时与动车相遇;(3)、高铁出发多长时间两车相距50km。
(1)、根据图像,高铁和动车的速度分别是;(2)、高铁出发多少小时与动车相遇;(3)、高铁出发多长时间两车相距50km。