2018年高考数学真题试卷(浙江卷)
试卷更新日期:2018-06-13 类型:高考真卷
一、选择题
-
1. 已知全集U={1,2,3,4,5},A={1,3},则 ( )
A、 B、{1,3} C、{2,4,5} D、{1,2,3,4,5}2. 双曲线 的焦点坐标是( )
A、(− ,0),( ,0) B、(−2,0),(2,0) C、(0,− ),(0, ) D、(0,−2),(0,2)3. 某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm3)是( ) A、2 B、4 C、6 D、84. 复数 (i为虚数单位)的共轭复数是( )
A、2 B、4 C、6 D、84. 复数 (i为虚数单位)的共轭复数是( )
A、1+i B、1−i C、−1+i D、−1−i5. 函数y= sin2x的图象可能是( )
A、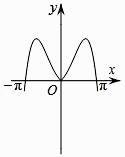 B、
B、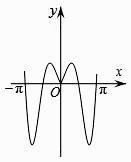 C、
C、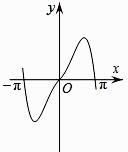 D、
D、 6. 已知平面α , 直线m , n满足m α , n α , 则“m∥n”是“m∥α”的( )
6. 已知平面α , 直线m , n满足m α , n α , 则“m∥n”是“m∥α”的( )
A、充分不必要条件 B、必要不充分条件 C、充分必要条件 D、既不充分也不必要条件7. 设0<p<1,随机变量ξ的分布列是ξ
0
1
2
P
则当p在(0,1)内增大时,( )
A、D(ξ)减小 B、D(ξ)增大 C、D(ξ)先减小后增大 D、D(ξ)先增大后减小8. 已知四棱锥S−ABCD的底面是正方形,侧棱长均相等,E是线段AB上的点(不含端点),设SE与BC所成的角为θ1 , SE与平面ABCD所成的角为θ2 , 二面角S−AB−C的平面角为θ3 , 则( )
A、θ1≤θ2≤θ3 B、θ3≤θ2≤θ1 C、θ1≤θ3≤θ2 D、θ2≤θ3≤θ19. 已知a , b , e是平面向量,e是单位向量.若非零向量a与e的夹角为 ,向量b满足b2−4e·b+3=0,则|a−b|的最小值是( )
A、 −1 B、 +1 C、2 D、2−10. 已知 成等比数列,且 .若 ,则( )
A、 B、 C、 D、二、填空题
-
11. 我国古代数学著作《张邱建算经》中记载百鸡问题:“今有鸡翁一,值钱五;鸡母一,值钱三;鸡雏三,值钱一。凡百钱,买鸡百只,问鸡翁、母、雏各几何?”设鸡翁,鸡母,鸡雏个数分别为 , , ,则 当 时, , .
12. 若 满足约束条件 则 的最小值是 , 最大值是 .
13. 在△ABC中,角A , B , C所对的边分别为a , b , c . 若a= ,b=2,A=60°,则sin B= , c= .
14. 二项式 的展开式的常数项是 .
15. 已知λ∈R,函数f(x)= ,当λ=2时,不等式f(x)<0的解集是 . 若函数f(x)恰有2个零点,则λ的取值范围是 .
16. 从1,3,5,7,9中任取2个数字,从0,2,4,6中任取2个数字,一共可以组成个没有重复数字的四位数.(用数字作答)
17. 已知点P(0,1),椭圆 +y2=m(m>1)上两点A , B满足 =2 ,则当m=时,点B横坐标的绝对值最大.
三、解答题
-
18. 已知角α的顶点与原点O重合,始边与x轴的非负半轴重合,它的终边过点P( ).
(Ⅰ)求sin(α+π)的值;
(Ⅱ)若角β满足sin(α+β)= ,求cosβ的值.
19. 如图,已知多面体ABCA1B1C1 , A1A , B1B , C1C均垂直于平面ABC , ∠ABC=120°,A1A=4,C1C=1,AB=BC=B1B=2.
(Ⅰ)证明:AB1⊥平面A1B1C1;
(Ⅱ)求直线AC1与平面ABB1所成的角的正弦值.
20. 已知等比数列{an}的公比q>1,且a3+a4+a5=28,a4+2是a3 , a5的等差中项.数列{bn}满足b1=1,数列{(bn+1−bn)an}的前n项和为2n2+n .(Ⅰ)求q的值;
(Ⅱ)求数列{bn}的通项公式.
