天津市宁河区2018届九年级下学期数学第一次联考试卷
试卷更新日期:2018-06-13 类型:中考模拟
一、单选题
-
1. 2sin45°的值等于()A、1 B、 C、 D、22. 下列图案中,可以看做是中心对称图形的有()
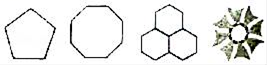 A、1个 B、2个 C、3个 D、4个3. 已知一个反比例函数的图象经过点A(3,﹣4),那么不在这个函数图象上的点是( )A、(﹣3,﹣4) B、(﹣3,4) C、(2,﹣6) D、( ,﹣12 )4. 如图是一个水平放置的圆柱形物体,中间有一细棒,则此几何体的俯视图是( )
A、1个 B、2个 C、3个 D、4个3. 已知一个反比例函数的图象经过点A(3,﹣4),那么不在这个函数图象上的点是( )A、(﹣3,﹣4) B、(﹣3,4) C、(2,﹣6) D、( ,﹣12 )4. 如图是一个水平放置的圆柱形物体,中间有一细棒,则此几何体的俯视图是( )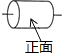 A、
A、 B、
B、 C、
C、 D、
D、 5. 函数y= 与y=ax2(a≠0)在同一平面直角坐标系中的图象可能是( )A、
5. 函数y= 与y=ax2(a≠0)在同一平面直角坐标系中的图象可能是( )A、 B、
B、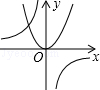 C、
C、 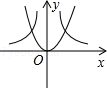 D、
D、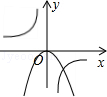 6. 如图,⊙O是△ABC的外接圆,已知∠ABO=30°,则∠ACB的大小为()
6. 如图,⊙O是△ABC的外接圆,已知∠ABO=30°,则∠ACB的大小为()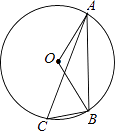 A、60° B、30° C、45° D、50°7. 已知圆的半径为R,这个圆的内接正六边形的面积为( )A、 R2 B、 R2 C、6R2 D、1.5R28. 若关于x的一元二次方程kx2﹣2x﹣1=0有两个不相等的实数根,则k的取值范围是( )A、k>﹣1 B、k>﹣1且k≠0 C、k<1 D、k<1且k≠09. 在平面直角坐标系中,点A的坐标为(﹣1,2),点B的坐标为(5,4),则线段AB的中点坐标为( )A、(2,3) B、(2,2.5) C、(3,3) D、(3,2.5)10. 如图,⊙O的直径AB垂直于弦CD,垂足为E,∠A=15°,半径为2,则弦CD的长为( )
A、60° B、30° C、45° D、50°7. 已知圆的半径为R,这个圆的内接正六边形的面积为( )A、 R2 B、 R2 C、6R2 D、1.5R28. 若关于x的一元二次方程kx2﹣2x﹣1=0有两个不相等的实数根,则k的取值范围是( )A、k>﹣1 B、k>﹣1且k≠0 C、k<1 D、k<1且k≠09. 在平面直角坐标系中,点A的坐标为(﹣1,2),点B的坐标为(5,4),则线段AB的中点坐标为( )A、(2,3) B、(2,2.5) C、(3,3) D、(3,2.5)10. 如图,⊙O的直径AB垂直于弦CD,垂足为E,∠A=15°,半径为2,则弦CD的长为( ) A、2 B、1 C、 D、411. 如图,点P是正方形ABCD内一点,将△ABP绕着B沿顺时针方向旋转到与△CBP′重合,若PB=3,则PP′的长为( )
A、2 B、1 C、 D、411. 如图,点P是正方形ABCD内一点,将△ABP绕着B沿顺时针方向旋转到与△CBP′重合,若PB=3,则PP′的长为( ) A、2 B、3 C、3 D、无法确定12. 已知二次函数y=﹣(x﹣h)2+1(为常数),在自变量x的值满足1≤x≤3的情况下,与其对应的函数值y的最大值为﹣5,则h的值为( )A、3﹣ 或1+ B、3﹣ 或3+ C、3+ 或1﹣ D、1﹣ 或1+
A、2 B、3 C、3 D、无法确定12. 已知二次函数y=﹣(x﹣h)2+1(为常数),在自变量x的值满足1≤x≤3的情况下,与其对应的函数值y的最大值为﹣5,则h的值为( )A、3﹣ 或1+ B、3﹣ 或3+ C、3+ 或1﹣ D、1﹣ 或1+二、填空题
-
13. 抛物线y=5(x﹣4)2+3的顶点坐标是 .
14. 在反比例函数y= 的图象上有两点A(x1 , y1),B(x2 , y2),当x1<0<x2时,有y1<y2 , 则m的取值范围是 .
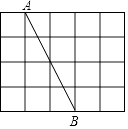
15. 如果圆锥的高为3,母线长为5,则圆锥的侧面积为 .16. 小凡沿着坡角为30°的坡面向下走了2米,那么他下降米.17. 如图所示,在边长为9的正三角形ABC中,BD=3,∠ADE=60°,则AE的长为.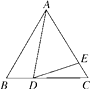 18. 如图,在每个小正方形的边长为1的网格中,点A,B均在格点上.
18. 如图,在每个小正方形的边长为1的网格中,点A,B均在格点上.(Ⅰ)线段AB的长为 .
(Ⅱ)请利用网格,用无刻度的直尺在AB上作出点P,使AP= ,并简要说明你的作图方法(不要求证明). .
三、解答题
-
19. 解下列方程:
(1)、x2+10x+25=0(2)、x2﹣x﹣1=0.20. 在一个黑色的布口袋里装着白、红、黑三种颜色的小球,它们除了颜色之外没有其它区别,其中白球2只、红球1只、黑球1只.袋中的球已经搅匀.
(1)、随机地从袋中摸出1只球,则摸出白球的概率是多少?
(2)、随机地从袋中摸出1只球,放回搅匀再摸出第二个球.请你用画树状图或列表的方法表示所有等可能的结果,并求两次都摸出白球的概率.21. 如图,直立于地面上的电线杆AB,在阳光下落在水平地面和坡面上的影子分别是BC、CD,测得BC=6米,CD=4米,∠BCD=150°,在D处测得电线杆顶端A的仰角为30°,试求电线杆的高度(结果保留根号)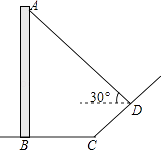 22. 某工厂为了对新研发的一种产品进行合理定价,将该产品按拟定的价格进行试销,通过对5天的试销情况进行统计,得到如下数据:
22. 某工厂为了对新研发的一种产品进行合理定价,将该产品按拟定的价格进行试销,通过对5天的试销情况进行统计,得到如下数据:单价(元/件)
30
34
38
40
42
销量(件)
40
32
24
20
16
(1)、通过对上面表格中的数据进行分析,发现销量y(件)与单价x(元/件)之间存在一次函数关系,求y关于x的函数关系式(不需要写出函数自变量的取值范围);
(2)、预计在今后的销售中,销量与单价仍然存在(2)中的关系,且该产品的成本是20元/件.为使工厂获得最大利润,该产品的单价应定为多少?(3)、为保证产品在实际试销中销售量不得低于30件,且工厂获得得利润不得低于400元,请直接写出单价x的取值范围.
23. 在Rt△ABC中,∠ACB=90°,BE平分∠ABC,D是边AB上一点,以BD为直径的⊙O经过点E,且交BC于点F. (1)、求证:AC是⊙O的切线;(2)、若BF=6,⊙O的半径为5,求CE的长.24. 如图①,将边长为2的正方形OABC如图①放置,O为原点.
(1)、求证:AC是⊙O的切线;(2)、若BF=6,⊙O的半径为5,求CE的长.24. 如图①,将边长为2的正方形OABC如图①放置,O为原点.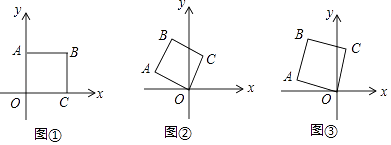
(Ⅰ)若将正方形OABC绕点O逆时针旋转60°时,如图②,求点A的坐标;
(Ⅱ)如图③,若将图①中的正方形OABC绕点O逆时针旋转75°时,求点B的坐标.
25. 如图,在平面直角坐标系中,直线y=x+3分别交x轴、y轴于A,C两点,抛物线y=ax2+bx+c(a≠0),经过A,C两点,与x轴交于点B(1,0).
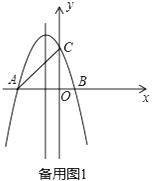
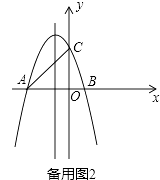 (1)、求抛物线的解析式;(2)、点D为直线AC上一点,点E为抛物线上一点,且D,E两点的横坐标都为2,点F为x轴上的点,若四边形ADEF是平行四边形,请直接写出点F的坐标;
(1)、求抛物线的解析式;(2)、点D为直线AC上一点,点E为抛物线上一点,且D,E两点的横坐标都为2,点F为x轴上的点,若四边形ADEF是平行四边形,请直接写出点F的坐标;
(3)、若点P是线段AC上的一个动点,过点P作x轴的垂线,交抛物线于点Q,连接AQ,CQ,求△ACQ的面积的最大值.