天津市红桥区2018届数学中考模拟试卷
试卷更新日期:2018-06-13 类型:中考模拟
一、单选题
-
1. cos30°的值为( )A、1 B、 C、 D、2. 下列图形中,可以看作是中心对称图形的是( )
A、 B、
B、 C、
C、 D、
D、 3. 用两块完全相同的长方体搭成如图所示的几何体,这个几何体的主视图是( )
3. 用两块完全相同的长方体搭成如图所示的几何体,这个几何体的主视图是( )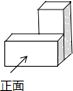 A、
A、 B、
B、 C、
C、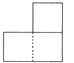 D、
D、 4. 在一个不透明的口袋中装有4个红球和若干个白球,它们除颜色外其它均相同,从袋中随机摸出一个球,记下颜色后放回.通过大量重复摸球试验后发现,摸到红球的频率在25%附近摆动,则口袋中的白球可能有( )
4. 在一个不透明的口袋中装有4个红球和若干个白球,它们除颜色外其它均相同,从袋中随机摸出一个球,记下颜色后放回.通过大量重复摸球试验后发现,摸到红球的频率在25%附近摆动,则口袋中的白球可能有( )
A、12个 B、13个 C、15个 D、16个5. 已知反比例函数y= 的图象经过点P(-1,2),则这个函数的图象位于( )A、第二、三象 B、第一、三象限 C、第二、四象限 D、第三、四象限6. 把抛物线y=﹣2x2先向右平移1个单位长度,再向上平移2个单位长度后,所得函数的表达式为( )A、y=﹣2(x+1)2+2 B、y=﹣2(x+1)2﹣2 C、y=﹣2(x﹣1)2+2 D、y=﹣2(x﹣1)2﹣27. 若2x2+1与4x2-2x-5互为相反数,则x为( )A、-1或 B、1或 C、1或 D、1或8. 一条公路弯道处是一段圆弧弧AB,点O是这条弧所在圆的圆心,点C是弧AB的中点,OC与AB相交于点D.已知AB=120m,CD=20m,那么这段弯道的半径为( )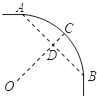 A、200m B、200 m C、100m D、100 m9. 如图,在平行四边形ABCD中,AB=10,AD=6,E是AD的中点,在AB上取一点F,使△CBF∽△CDE,则BF的长是( )
A、200m B、200 m C、100m D、100 m9. 如图,在平行四边形ABCD中,AB=10,AD=6,E是AD的中点,在AB上取一点F,使△CBF∽△CDE,则BF的长是( )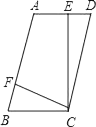 A、5 B、8.2 C、6.4 D、1.810. 在△ABC中,AB=AC=13,BC=24,则tanB等于( )A、 B、 C、 D、11. 如图,A,B,C,D四个点均在⊙O上,∠AOD=50°,AO∥DC,则∠B的度数为( )
A、5 B、8.2 C、6.4 D、1.810. 在△ABC中,AB=AC=13,BC=24,则tanB等于( )A、 B、 C、 D、11. 如图,A,B,C,D四个点均在⊙O上,∠AOD=50°,AO∥DC,则∠B的度数为( )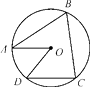 A、50° B、55° C、60° D、65°12. 如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论:①a-b+c>0;②3a+b=0;③b2=4a(c-n);④一元二次方程ax2+bx+c=n-1有两个不相等的实数根.其中正确结论的个数是( )
A、50° B、55° C、60° D、65°12. 如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论:①a-b+c>0;②3a+b=0;③b2=4a(c-n);④一元二次方程ax2+bx+c=n-1有两个不相等的实数根.其中正确结论的个数是( )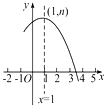 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
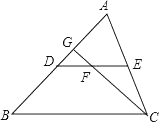
13. 一元二次方程x2+px﹣2=0的一个根为2,则p的值 .14. 一个不透明的布袋中有分别标着数字1,2,3,4的四个乒乓球,现从袋中随机摸出两个乒乓球,则这两个乒乓球上的数字之和大于5的概率为15. 如图,DE是△ABC的中位线,F是DE的中点,CF的延长线交AB于G,AB=6,则AG= .
 16. 如图,AB,AC分别为⊙O的内接正六边形,内接正方形的一边,BC是圆内接n边形的一边,则n等于 .
16. 如图,AB,AC分别为⊙O的内接正六边形,内接正方形的一边,BC是圆内接n边形的一边,则n等于 .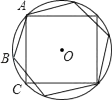 17. 如图,在△ABC中,∠CAB=75°,在同一平面内,将△ABC绕点A旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′=
17. 如图,在△ABC中,∠CAB=75°,在同一平面内,将△ABC绕点A旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′=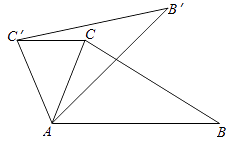 18. 如图,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,F是CD上一点,DF=1,在对角线AC上有一点P,连接PE,PF,则PE+PF的最小值为 .
18. 如图,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,F是CD上一点,DF=1,在对角线AC上有一点P,连接PE,PF,则PE+PF的最小值为 .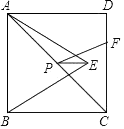
三、解答题
-
19. 关于x的一元二次方程(2m+1)x2+4mx+2m﹣3=0
(Ⅰ)当m= 时,求方程的实数根;
(Ⅱ)若方程有两个不相等的实数根,求实数m的取值范围;
20. 如图,已知反比例函数y= (k≠0)的图象经过点A(﹣2,m),过点A作AB⊥x轴于点B,且△AOB的面积为4.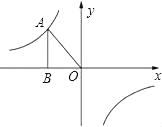
(Ⅰ)求k和m的值;
(Ⅱ)设C(x,y)是该反比例函数图象上一点,当1≤x≤4时,求函数值y的取值范围.
21. 如图,AB是⊙O的直径,OD垂直于弦AC于点E,且交⊙O于点D,F是BA延长线上一点,若∠CDB=∠BFD.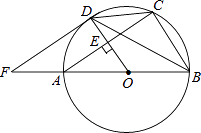 (1)、求证:FD是⊙O的一条切线;(2)、若AB=10,AC=8,求DF的长.22. 如图,在一条笔直公路BD的正上方A处有一探测仪,AD=24m,∠D=90°,一辆轿车从B点匀速向D点行驶,测得∠ABD=31°,2秒后到达C点,测得∠ACD=50°.
(1)、求证:FD是⊙O的一条切线;(2)、若AB=10,AC=8,求DF的长.22. 如图,在一条笔直公路BD的正上方A处有一探测仪,AD=24m,∠D=90°,一辆轿车从B点匀速向D点行驶,测得∠ABD=31°,2秒后到达C点,测得∠ACD=50°.
(Ⅰ)求B,C两点间的距离(结果精确到1m);
(Ⅱ)若规定该路段的速度不得超过15m/s,判断此轿车是否超速.
参考数据:tan31°≈0.6,tan50°≈1.2.
23. 某商场试销一种成本为每件60元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于50%.经试销发现,销售量P(件)与销售单价x(元)符合一次函数关系,当销售单价为65元时销售量为55件,当销售单价为75元时销售量为45件.(Ⅰ)求P与x的函数关系式;
(Ⅱ)若该商场获得利润为y元,试写出利润y与销售单价x之间的关系式;
(Ⅲ)销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
24. 在平面直角坐标系中,O为原点,点A(1,0),点B(0, ),把△ABO绕点O顺时针旋转,得A′B′O,记旋转角为α.
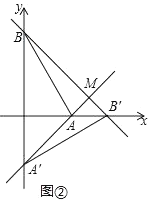
(Ⅰ)如图①,当α=30°时,求点B′的坐标;
(Ⅱ)设直线AA′与直线BB′相交于点M.
如图②,当α=90°时,求点M的坐标;
②点C(﹣1,0),求线段CM长度的最小值.(直接写出结果即可)
25. 已知:如图,直线y=kx+2与x轴正半轴相交于A(t,0),与y轴相交于点B,抛物线y=﹣x2+bx+c经过点A和点B,点C在第三象象限内,且AC⊥AB,tan∠ACB= .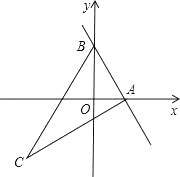 (1)、当t=1时,求抛物线的表达式;(2)、试用含t的代数式表示点C的坐标;(3)、如果点C在这条抛物线的对称轴上,求t的值.
(1)、当t=1时,求抛物线的表达式;(2)、试用含t的代数式表示点C的坐标;(3)、如果点C在这条抛物线的对称轴上,求t的值.