天津市河东区2018届数学中考模拟试卷
试卷更新日期:2018-06-13 类型:中考模拟
一、单选题
-
1. 2cos60°的值等于( )A、1 B、 C、 D、22. 下列标志中,可以看作是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 据《天津日报》报道,天津市社会保障制度更加成熟完善,截止2017年4月末,累计发放社会保障卡12630000张.将12630000用科学记数法表示为( )
3. 据《天津日报》报道,天津市社会保障制度更加成熟完善,截止2017年4月末,累计发放社会保障卡12630000张.将12630000用科学记数法表示为( )
A、0.1263×108 B、1.263×107 C、12.63×106 D、126.3×1054. 如图,某个反比例函数的图象经过点P,则它的解析式为( ) A、y= (x>0) B、y=- (x>0) C、y= (x<0) D、y=- (x<0)5. 如图,从左面观察这个立体图形,能得到的平面图形是( )
A、y= (x>0) B、y=- (x>0) C、y= (x<0) D、y=- (x<0)5. 如图,从左面观察这个立体图形,能得到的平面图形是( )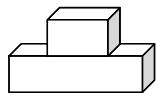 A、
A、 B、
B、 C、
C、 D、
D、 6. 如图,⊙O中,弦AB、CD相交于点P,若∠A=30°,∠APD=70°,则∠B等于( )
6. 如图,⊙O中,弦AB、CD相交于点P,若∠A=30°,∠APD=70°,则∠B等于( )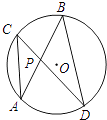 A、30° B、35° C、40° D、50°7. 比较2, , 的大小,正确的是( )
A、30° B、35° C、40° D、50°7. 比较2, , 的大小,正确的是( )
A、2< < B、2< < C、 <2< D、 < <28. 如图,在边长为2的正方形ABCD中,M为边AD的中点,延长MD至点E,使ME=MC,以DE为边作正方形DEFG,点G在边CD上,则DG的长为( ) A、 B、 C、 D、9. 如图,将△ABC绕点B顺时针旋转60°得△DBE,点C的对应点E恰好落在AB延长线上,连接AD.下列结论一定正确的是( )
A、 B、 C、 D、9. 如图,将△ABC绕点B顺时针旋转60°得△DBE,点C的对应点E恰好落在AB延长线上,连接AD.下列结论一定正确的是( )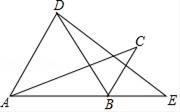 A、∠ABD=∠E B、∠CBE=∠C C、AD∥BC D、AD=BC10. 若点A(-5,y1),B(-3,y2),C(2,y3)在反比例函数y= 的图象上,则y1 , y2 , y3的大小关系是( )
A、∠ABD=∠E B、∠CBE=∠C C、AD∥BC D、AD=BC10. 若点A(-5,y1),B(-3,y2),C(2,y3)在反比例函数y= 的图象上,则y1 , y2 , y3的大小关系是( )
A、y1<y3<y2 B、y1<y2<y3 C、y3<y2<y1 D、y2<y1<y311. 如图,已知▱ABCD中,AE⊥BC于点E,以点B为中心,取旋转角等于∠ABC,把△BAE顺时针旋转,得到△BA′E′,连接DA′.若∠ADC=60°,∠ADA′=50°,则∠DA′E′的大小为( ) A、130° B、150° C、160° D、170°
A、130° B、150° C、160° D、170°二、填空题
-
12. 计算( )( )的结果等于 .
13. 如果反比例函数y= (a为常数)的图象,在每一个象限内,y随x的增大而减小,写出一个符合条件的a的值为 .14. 一个盒子中装有2个白球,5个红球,从这个盒子中随机摸出一个球,是红球的概率为 .15. 如图,矩形ABCD中,AD=2,AB=5,P为CD边上的动点,当△ADP与△BCP相似时,DP= . 16. 二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:①4ac﹣b2<0;②4a+c<2b;③3b+2c<0;④m(am+b)+b<a(m≠﹣1),其中正确结论的是(只填序号).
16. 二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:①4ac﹣b2<0;②4a+c<2b;③3b+2c<0;④m(am+b)+b<a(m≠﹣1),其中正确结论的是(只填序号).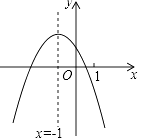 17. 如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论:
17. 如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论:①∠EBG=45°;②△DEF∽△ABG;③S△ABG= S△FGH;④AG+DF=FG.
其中正确的是 . (把所有正确结论的序号都选上)

三、解答题
-
18. 解方程:3x(x﹣2)=2(2﹣x).
19. 如图,转盘A的三个扇形面积相等,分别标有数字1,2,3,转盘B的四个扇形面积相等,分别有数字1,2,3,4.转动A、B转盘各一次,当转盘停止转动时,将指针所落扇形中的两个数字相乘(当指针落在四个扇形的交线上时,重新转动转盘). (1)、用树状图或列表法列出所有可能出现的结果;(2)、求两个数字的积为奇数的概率.20. 已知△ABC中,BC=5,以BC为直径的⊙O交AB边于点D.
(1)、用树状图或列表法列出所有可能出现的结果;(2)、求两个数字的积为奇数的概率.20. 已知△ABC中,BC=5,以BC为直径的⊙O交AB边于点D. (1)、如图1,连接CD,则∠BDC的度数为;
(1)、如图1,连接CD,则∠BDC的度数为;
(2)、如图2,若AC与⊙O相切,且AC=BC,求BD的长;(3)、如图3,若∠A=45°,且AB=7,求BD的长.21. 小明在热气球A上看到横跨河流两岸的大桥BC,并测得B,C两点的俯角分别为45°,36°.已知大桥BC与地面在同一水平面上,其长度为100m.请求出热气球离地面的高度(结果保留小数点后一位).参考数据:tan36°≈0.73. 22. 水果店张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤.通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤.为了保证每天至少售出260斤,张阿姨决定降价销售.
22. 水果店张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤.通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤.为了保证每天至少售出260斤,张阿姨决定降价销售.
(1)、若将这种水果每斤的售价降低x元,则每天的销售量是斤(用含x的代数式表示);
(2)、销售这种水果要想每天盈利300元,张阿姨需将每斤的售价降低多少元?
(3)、当每斤的售价定为多少元时,每天获利最大?最大值为多少?23. 如图,点A是x轴非负半轴上的动点,点B坐标为(0,4),M是线段AB的中点,将点M绕点A顺时针方向旋转90°得到点C,过点C作x轴的垂线,垂足为F,过点B作y轴的垂线与直线CF相交于点E,连接AC,BC,设点A的横坐标为t.
(Ⅰ)当t=2时,求点M的坐标;
(Ⅱ)设ABCE的面积为S,当点C在线段EF上时,求S与t之间的函数关系式,并写出自变量t的取值范围;
(Ⅲ)当t为何值时,BC+CA取得最小值.
24. 在平面直角坐标系xOy中,二次函数y=mx2﹣(m+n)x+n(m<0)的图象与y轴正半轴交于A点. (1)、求证:该二次函数的图象与x轴必有两个交点;(2)、设该二次函数的图象与x轴的两个交点中右侧的交点为点B,若∠ABO=45°,将直线AB向下平移2个单位得到直线l,求直线l的解析式;(3)、在(2)的条件下,设M(p,q)为二次函数图象上的一个动点,当﹣3<p<0时,点M关于x轴的对称点都在直线l的下方,求m的取值范围.
(1)、求证:该二次函数的图象与x轴必有两个交点;(2)、设该二次函数的图象与x轴的两个交点中右侧的交点为点B,若∠ABO=45°,将直线AB向下平移2个单位得到直线l,求直线l的解析式;(3)、在(2)的条件下,设M(p,q)为二次函数图象上的一个动点,当﹣3<p<0时,点M关于x轴的对称点都在直线l的下方,求m的取值范围.