山东省青岛市2018届数学中考模拟试卷
试卷更新日期：2018-06-13 类型：中考模拟
一、单选题
-
1. ﹣ 的绝对值是（ ）A、﹣ B、﹣ C、 D、52. 某种计算机完成一次基本运算的时间约为0.000 000 001 s，把0.000 000 001 s用科学记数法可表示为（ ）A、0.1×10－8 s B、0.1×10－9 s C、1×10－8 s D、1×10－9 s3. 下列四个图形中，既是轴对称图形又是中心对称图形的是（ ）A、
B、
C、
D、
4. 计算a•a5﹣（2a3）2的结果为（ ）A、a6﹣2a5 B、﹣a6 C、a6﹣4a5 D、﹣3a65. 如图，线段AB经过平移得到线段A1B1 ， 其中点A，B的对应点分别为点A1 ， B1 ， 这四个点都在格点上．若线段AB上有一个点P(a，b)，则点P在A1B1上的对应点P′的坐标为（ ）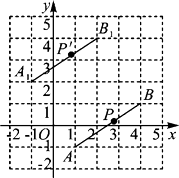
A、(a－2，b＋3) B、(a－2，b－3) C、(a＋2，b＋3) D、(a＋2，b－3)6. A，B两地相距180km，新修的高速公路开通后，在A，B两地间行驶的长途客车平均车速提高了50%，而从A地到B地的时间缩短了1h．若设原来的平均车速为xkm/h，则根据题意可列方程为（ ）
A、 ﹣ =1 B、 ﹣ =1 C、 ﹣ =1 D、 ﹣ =17. 如图，一扇形纸扇完全打开后，外侧两竹条AB和AC的夹角为120°，AB长为25cm，贴纸部分的宽BD为15cm，若纸扇两面贴纸，则贴纸的面积为（ ）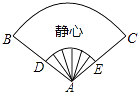
A、175πcm2 B、350πcm2 C、 πcm2 D、150πcm28. 如图，正比例函数y1＝k1x的图象与反比例函数y2＝ 的图象相交于A，B两点，其中点A的横坐标为2，当y1＞y2时，x的取值范围是（ ）
A、x＜－2或x＞2 B、x＜－2或0＜x＜2 C、－2＜x＜0或0＜x＜2 D、－2＜x＜0或x＞2二、填空题
-
9. 计算： ＝ ．10. “万人马拉松”活动组委会计划制作运动衫分发给参与者，为此，调查了部分参与者，以决定制作橙色、黄色、白色、红色四种颜色运动衫的数量．根据得到的调查数据，绘制成如图所示的扇形统计图．若本次活动共有12000名参与者，则估计其中选择红色运动衫的约有名．
11. 如图AB是⊙O的直径，C，D是⊙O上的两点，若∠BCD=28°，则∠ABD= ．
12. 把一个长、宽、高分别为3cm、2cm、1cm的长方体铜块铸成一个圆柱体铜块，则该圆柱体铜块的底面积S(cm2)与高h(cm)之间的函数关系式为.
13. 如图，在正方形ABCD中，对角线AC与BD相交于点O，E为BC上一点，CE=5，F为DE的中点．若△CEF的周长为18，则OF的长为 ．
14. 如图，以边长为20cm的正三角形纸板的各顶点为端点，在各边上分别截取4cm长的六条线段，过截得的六个端点作所在边的垂线，形成三个有两个直角的四边形．把它们沿图中 虛线剪掉，用剩下的纸板折成一个底为正三角形的无盖柱形盒子，则它的容积为cm3 ．
三、解答题
-
15. 已知：线段a及∠ACB．
求作：⊙O，使⊙O在∠ACB的内部，CO=a，且⊙O与∠ACB的两边分别相切．
16. 计算
(1)、化简：（ +n）÷ ；(2)、关于x的一元二次方程2x2+3x﹣m=0有两个不相等的实数根，求m的取值范围．
17. 小颖和小丽做“摸球”游戏：在一个不透明的袋子中装有编号为1～4的四个球(除编号外都相同)，从中随机摸出一个球，记下数字后放回，再从中摸出一个球，记下数字．若两次数字之和大于5，则小颖胜，否则小丽胜．这个游戏对双方公平吗？请说明理由．
18. 小明在热气球A上看到正前方横跨河流两岸的大桥BC，并测得B、C两点的俯角分别为45°、35°.已知大桥BC与地面在同一水平面上，其长度为100m，请求出热气球离地面的高度．（结果保留整数）（参考数据：sin35°≈ ，cos35°≈ ，tan35°≈ ）
19. 甲、乙两名队员参加射击训练，成绩分别绘制成下列两个统计图：
根据以上信息，整理分析数据如下：
平均成绩(环)
中位数(环)
众数(环)
方差
甲
a
7
7
1.2
乙
7
b
8
c
(1)、写出表格中a，b，c的值；赛，你认为应选哪名队员？
(2)、分别运用表中的四个统计量，简要分析这两名队员的射击成绩，若选派其中一名参赛，你认为应选哪名队员？20. 某厂制作甲、乙两种环保包装盒，已知同样用6m材料制成甲盒的个数比制成乙盒的个数少2个，且制成一个甲盒比制成一个乙盒需要多用20%的材料．
(1)、求制作每个甲盒、乙盒各用多少米材料？(2)、如果制作甲、乙两种包装盒共3000个，且甲盒的数量不少于乙盒数量的2倍，那么请写出所需要材料的总长度l（m）与甲盒数量n（个）之间的函数关系式，并求出最少需要多少米材料？
21. 已知：如图，在▱ABCD中，E，F分别是边AD，BC上的点，且AE=CF，直线EF分别交BA的延长线、DC的延长线于点G，H，交BD于点O．
(1)、求证：△ABE≌△CDF；(2)、连接DG，若DG=BG，则四边形BEDF是什么特殊四边形？请说明理由．22. 如图，隧道的截面由抛物线和长方形构成，长方形的长是12m，宽是4m．按照图中所示的直角坐标系，抛物线可以用y=﹣ x2+bx+c表示，且抛物线的点C到墙面OB的水平距离为3m时，到地面OA的距离为 m．
(1)、求该抛物线的函数关系式，并计算出拱顶D到地面OA的距离；(2)、一辆货运汽车载一长方体集装箱后高为6m，宽为4m，如果隧道内设双向行车道，那么这辆货车能否安全通过？
(3)、在抛物线型拱壁上需要安装两排灯，使它们离地面的高度相等，如果灯离地面的高度不超过8m，那么两排灯的水平距离最小是多少米？
23. 问题提出：用n根相同的木棒搭一个三角形（木棒无剩余），能搭成多少种不同的等腰三角形？问题探究：不妨假设能搭成m种不同的等腰三角形，为探究m与n之间的关系，我们可以从特殊入手，通过试验、观察、类比，最后归纳、猜测得出结论．
探究一：
①用3根相同的木棒搭成一个三角形，能搭成多少种不同的三角形？
此时，显然能搭成一种等腰三角形。所以，当n=3时，m=1
②用4根相同的木棒搭成一个三角形，能搭成多少种不同的三角形？
只可分成1根木棒、1根木棒和2根木棒这一种情况，不能搭成三角形
所以，当n=4时，m=0
③用5根相同的木棒搭成一个三角形，能搭成多少种不同的三角形？
若分成1根木棒、1根木棒和3根木棒，则不能搭成三角形
若分为2根木棒、2根木棒和1根木棒，则能搭成一种等腰三角形
所以，当n=5时，m=1
④用6根相同的木棒搭成一个三角形，能搭成多少种不同的三角形？
若分成1根木棒、1根木棒和4根木棒，则不能搭成三角形
若分为2根木棒、2根木棒和2根木棒，则能搭成一种等腰三角形
所以，当n=6时，m=1
综上所述，可得表①
n
3
4
5
6
m
1
0
1
1
探究二：
(1)、用7根相同的木棒搭成一个三角形，能搭成多少种不同的等腰三角形？（仿照上述探究方法，写出解答过程，并把结果填在表②中）
(2)、分别用8根、9根、10根相同的木棒搭成一个三角形，能搭成多少种不同的等腰三角形？（只需把结果填在表②中）n
7
8
9
10
m
你不妨分别用11根、12根、13根、14根相同的木棒继续进行探究，……
解决问题：用n根相同的木棒搭一个三角形（木棒无剩余），能搭成多少种不同的等腰三角形？
（设n分别等于4k-1、4k、4k+1、4k+2，其中k是整数，把结果填在表③中）
n
4k-1
4k
4k+1
4k+2
m
(3)、问题应用：用2016根相同的木棒搭一个三角形（木棒无剩余），能搭成多少种不同的等腰三角形？（要求写出解答过程）其中面积最大的等腰三角形每个腰用了多少根木棒。（只填结果）24. 已知：如图，在矩形ABCD中，AB=6cm，BC=8cm，对角线AC，BD交于点0．点P从点A出发，沿方向匀速运动，速度为1cm/s；同时，点Q从点D出发，沿DC方向匀速运动，速度为1cm/s；当一个点停止运动时，另一个点也停止运动．连接PO并延长，交BC于点E，过点Q作QF∥AC，交BD于点F．设运动时间为t（s）（0＜t＜6），解答下列问题：
(1)、当t为何值时，△AOP是等腰三角形？
(2)、设五边形OECQF的面积为S（cm2），试确定S与t的函数关系式；
(3)、在运动过程中，是否存在某一时刻t，使S五边形S五边形OECQF：S△ACD=9：16？若存在，求出t的值；若不存在，请说明理由；
(4)、在运动过程中，是否存在某一时刻t，使OD平分∠COP？若存在，求出t的值；若不存在，请说明理由．