山东省济南市天桥区2018届九年级下学期数学中考一模试卷
试卷更新日期:2018-06-13 类型:中考模拟
一、单选题
-
1. 7的相反数是( )A、 7 B、-7 C、 D、2. 如图,下列几何体是由4个相同的小正方体组合而成的,从左面看得到的平面图形是下列选项中的( )
 A、
A、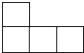 B、
B、 C、
C、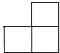 D、
D、 3. 我国每年的淡水为27500亿m3 , 人均仅居世界第110位,用科学记数法表示27500为( )A、275×102 B、27.5×103 C、2.75×104 D、0.275×1054. 如图,直线a∥b,∠1=70°,那么∠2的度数是( )
3. 我国每年的淡水为27500亿m3 , 人均仅居世界第110位,用科学记数法表示27500为( )A、275×102 B、27.5×103 C、2.75×104 D、0.275×1054. 如图,直线a∥b,∠1=70°,那么∠2的度数是( )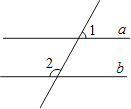 A、130° B、110° C、70° D、80°5. 下列计算正确的是( )A、(a5)2=a10 B、x16÷x4=x4 C、2a2+3a2=6a4 D、b3•b3=2b36. 将点A(﹣1,2)向右平移4个单位长度,再向下平移3个单位长度,则平移后点的坐标是( )
A、130° B、110° C、70° D、80°5. 下列计算正确的是( )A、(a5)2=a10 B、x16÷x4=x4 C、2a2+3a2=6a4 D、b3•b3=2b36. 将点A(﹣1,2)向右平移4个单位长度,再向下平移3个单位长度,则平移后点的坐标是( )
A、(3,1) B、(﹣3,﹣1) C、(3,﹣1) D、(﹣3,1)7. 下列图形中,既是轴对称图形,又是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 8. 如图所示,用扇形统计图反映地球上陆地面积与海洋面积所占比例时,陆地面积所对应的圆心角是108°,当宇宙中一块陨石落在地球上,则落在陆地上的概率是( ) .
8. 如图所示,用扇形统计图反映地球上陆地面积与海洋面积所占比例时,陆地面积所对应的圆心角是108°,当宇宙中一块陨石落在地球上,则落在陆地上的概率是( ) . A、0.2 B、0.3 C、0.4 D、0.59. 解分式方程 分以下几步,其中错误的一步是( )A、方程两边分式的最简公分母是(x-1)(x+1) B、方程两边都乘以(x-1)(x+1),得整式方程2(x-1)+3(x+1)=6 C、解这个整式方程,得x=1 D、原方程的解为x=110. 如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为F,则EF的长为( )
A、0.2 B、0.3 C、0.4 D、0.59. 解分式方程 分以下几步,其中错误的一步是( )A、方程两边分式的最简公分母是(x-1)(x+1) B、方程两边都乘以(x-1)(x+1),得整式方程2(x-1)+3(x+1)=6 C、解这个整式方程,得x=1 D、原方程的解为x=110. 如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为F,则EF的长为( ) A、1 B、 C、4-2 D、3 -411. 把所有正偶数从小到大排列,并按如下规律分组:
A、1 B、 C、4-2 D、3 -411. 把所有正偶数从小到大排列,并按如下规律分组:第一组:2,4;
第二组:6,8,10,12;
第三组:14,16,18,20,22,24
第四组:26,28,30,32,34,36,38,40
……
则现有等式Am=(i,j)表示正偶数m是第i组第j个数(从左到又数),如A10=(2,3),则A2018=( )
A、(31,63) B、(32,17) C、(33,16) D、(34,2)12. 某校校园内有一个大正方形花坛,如图甲所示,它由四个边长为3米的小正方形组成,且每个小正方形的种植方案相同.其中的一个小正方形ABCD如图乙所示,DG=1米,AE=AF=x米,在五边形EFBCG区域上种植花卉,则大正方形花坛种植花卉的面积y与x的函数图象大致是( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
13. 计算:|-5+3 |=14. 分解因式:3x2-12= .15. 已知一组数据0,2,x,4,5的众数是4,那么这组数据的中位数是.16. 如图,△ABC的顶点都是正方形网格中的格点,则tan∠ABC=.
 17. 将矩形ABCD按如图所示的方式折叠,得到菱形AECF,若AB=3,则菱形AECF的周长为 .
17. 将矩形ABCD按如图所示的方式折叠,得到菱形AECF,若AB=3,则菱形AECF的周长为 . 18. 如图,在平面直角坐标系中,反比例函数y= (x>0)的图象上,有一动点P,以点P为圆心,以一个定值R为半径作⊙P在点P运动过程中,若⊙P与直线y=-x+4有且只有3次相切时,则定值R为.
18. 如图,在平面直角坐标系中,反比例函数y= (x>0)的图象上,有一动点P,以点P为圆心,以一个定值R为半径作⊙P在点P运动过程中,若⊙P与直线y=-x+4有且只有3次相切时,则定值R为.
三、解答题
-
19. 计算: +2-1-2cos60°+(π-3)020. 解不等式组 并将解集在数轴上表示出来.21. 如图:点C是AE的中点,∠A=∠ECD,AB=CD,求证:∠B=∠D.
 22. 为了奖励优秀班集体,学校购买了若干副乒乓球拍和羽毛球拍,购买2副乒乓球拍和1副羽毛球拍共需116元,购买3幅乒乓球拍和2幅羽毛球拍共需204元.
22. 为了奖励优秀班集体,学校购买了若干副乒乓球拍和羽毛球拍,购买2副乒乓球拍和1副羽毛球拍共需116元,购买3幅乒乓球拍和2幅羽毛球拍共需204元.
(1)、每副乒乓球拍和羽毛球拍的单价各是多少元?(2)、若学校购买5副乒乓球拍和3副羽毛球拍,一共应支出多少元?23. 我区实施课堂教学改革后,学生的自主学习、合作交流能力有很大提高,为了解学生自主学习、合作交流的具体情况,张老师对本班部分学生进行了为期半个月的跟踪调查,并将调查结果分成四类,A:特别好;B:好;C:一般;D:较差;绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题: (1)、本次调查中,张老师一共调查了几名同学;
(1)、本次调查中,张老师一共调查了几名同学;
(2)、将上面的条形统计图补充完整;(3)、为了共同进步,张老师从被调查的A类和D类学生中分别选取一位同学进行“一帮一”互助学习,请用列表法或画树形图的方法求出所选两位同学恰好是一男一女的概率.24. 甲、乙两家绿化养护公司各自推出了校园绿化养护服务的收费方案.甲公司方案:每月的养护费用y(元)与绿化面积x(平方米)的关系如图所示.
乙公司方案:绿化面积不超过1000平方米时,每月收取费用5500元;绿化面积超过1000平方米时,超过的部分每月每平方米加收4元.
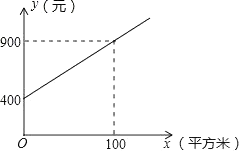 (1)、求如图所示的y与x的函数表达式;
(1)、求如图所示的y与x的函数表达式;
(2)、如果某学校目前的绿化面积是1200平方米.那么选择哪家公司的服务比较划算.
25. 如图,⊙O的直径AB=10,弦AC=6,∠ACB的平分线交⊙O于点D,过点D作DE∥AB交CA延长线于点E,连接AD,BD. (1)、△ABD的面积是多少
(1)、△ABD的面积是多少
(2)、求证:DE是⊙O的切线:(3)、求线段DE的长.26. 综合题
(1)、【探索发现】如图①,是一张直角三角形纸片,∠B=90°,小明想从中剪出一个以∠B为内角且面积最大的矩形,经过多次操作发现,当沿着中位线DE、EF剪下时,所得的矩形的面积最大,随后,他通过证明验证了其正确性,并得出:矩形的最大面积与原三角形面积的比值为多少.
 (2)、【拓展应用】
(2)、【拓展应用】如图②,在△ABC中,BC=a,BC边上的高AD=h,矩形PQMN的顶点P、N分别在边AB、AC上,顶点Q、M在边BC上,则矩形PQMN面积的最大值为多少.(用含a,h的代数式表示)
(3)、【灵活应用】如图③,有一块“缺角矩形”ABCDE,AB=32,BC=40,AE=20,CD=16,小明从中剪出了一个面积最大的矩形(∠B为所剪出矩形的内角),求该矩形的面积.
(4)、【实际应用】如图④,现有一块四边形的木板余料ABCD,经测量AB=50cm,BC=108cm,CD=60cm,且tanB=tanC= ,木匠徐师傅从这块余料中裁出了顶点M、N在边BC上且面积最大的矩形PQMN,求该矩形的面积.
27. 如图1,在平面直角坐标系中,已知抛物线y=ax2+bx﹣5与x轴交于A(﹣1,0),B(5,0)两点,与y轴交于点C. (1)、求抛物线的函数表达式;(2)、如图2,CE∥x轴与抛物线相交于点E,点H是直线CE下方抛物线上的动点,过点H且与y轴平行的直线与BC,CE分别相交于点F,G,试探究当点H运动到何处时,四边形CHEF的面积最大,求点H的坐标;(3)、若点K为抛物线的顶点,点M(4,m)是该抛物线上的一点,在x轴,y轴上分别找点P,Q,使四边形PQKM的周长最小,求出点P,Q的坐标.
(1)、求抛物线的函数表达式;(2)、如图2,CE∥x轴与抛物线相交于点E,点H是直线CE下方抛物线上的动点,过点H且与y轴平行的直线与BC,CE分别相交于点F,G,试探究当点H运动到何处时,四边形CHEF的面积最大,求点H的坐标;(3)、若点K为抛物线的顶点,点M(4,m)是该抛物线上的一点,在x轴,y轴上分别找点P,Q,使四边形PQKM的周长最小,求出点P,Q的坐标.