内蒙古鄂尔多斯市东胜区2018届数学中考一模试卷
试卷更新日期：2018-06-13 类型：中考模拟
一、单选题
-
1. 如果一个数的绝对值是2，那么这个数是（ ）A、2 B、﹣2 C、2或﹣2 D、2. “激情盛会，和谐亚洲”第16届亚运会在广州举行，广州亚运城的建筑面积约是358000平方米，将358000用科学记数法表示（保留两个有效数字）为（ ）A、3.5×105 B、3.6×105 C、3.58×105 D、4×1053. 下列等式成立的是（ ）
A、2﹣1=﹣2 B、（a2）3=a5 C、a6÷a3=a2 D、﹣2（x﹣1）=﹣2x+24. 如图，将一副三角板按图中方式叠放，则角α等于（ ）
A、30° B、45° C、60° D、75°5. 关于直线y=﹣2x+1，下列叙述正确的是（ ）
A、图象过点（1，0） B、图象经过一，二，四象限 C、y随x的增大而增大 D、是正比例函数y=﹣2x的图象向右平移一个单位得到的6. 一组数据：3，2，1，2，2的众数，中位数，方差分别是（ ）A、2，1，0.4 B、2，2，0.4 C、3，1，2 D、2，1，0.27. 如图，是一个几何体的三视图，根据图中标注的数据可求得这个几何体的体积为（ ）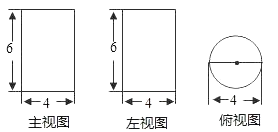
A、24π B、32π C、36π D、48π8. 已知：如右图，O为圆锥的顶点，M为底面圆周上一点，点P在OM上，一只蚂蚁从点P出发绕圆锥侧面爬行回到点P时所经过的最短路径的痕迹如图．若沿OM将圆锥侧面剪开并展平，所得侧面展开图是（ ）
A、
B、
C、
D、
9. 均匀地向一个容器注水，最后把容器注满．在注水过程中，水面高度h随时间t的变化规律如图所示（图中OABC为一折线），则这个容器的形状为（ ）
A、
B、
C、
D、
10. 如图，已知A1（1，0），A2（1，1），A3（﹣1，1），A4（﹣1，﹣1），A5（2，﹣1），则点A2012的坐标为（ ）
A、（2012，2012） B、（﹣1006，﹣1006） C、（﹣503，﹣503） D、（﹣502，﹣502）二、填空题
-
11. 函数y= 中，自变量x的取值范围是 ．
12. 分解因式：3x3-6x2+3x= ．13. 方程x2+4x﹣1=0的解是： ．
14. 如图，已知AB是⊙O的直径，CD是⊙O的切线，C为切点，且∠BAC=50°，则∠ACD=°．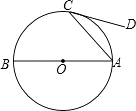
15. 已知圆上一段弧长为6π，它所对的圆心角为120°，则该圆的半径为 ．
16. 如图，在周长为20cm的▱ABCD中，AB≠AD，AC，BD相交于点O，OE⊥BD交AD于E，则△ABE的周长为cm．
17. 如图1，把一个长为m、宽为n的长方形（m＞n）沿虚线剪开，拼接成图2，成为在一角去掉一个小正方形后的一个大正方形，则去掉的小正方形的边长（用含m，n的式子表示）为 ．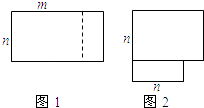
18. 如图，一艘海轮位于灯塔P的东北方向，距离灯塔 海里的A处，它沿正南方向航行一段时间后，到达位于灯塔P的南偏东30°方向上的B处，则海轮行驶的路程AB为海里（结果保留根号）．
三、解答题
-
19. 解答题
(1)、计算： ．(2)、如图，一次函数y=x+b与反比例函数 在第一象限的图象交于点B，且点B的横坐标为1，过点B作y轴的垂线，C为垂足，若S△BCO= ，求一次函数和反比例函数的解析式．
20. 学习了统计知识后，小明就本班同学的上学方式进行了一次调查统计．图（1）和图（2）是他通过采集数据后，绘制的两幅不完整的统计图．请你根据图中提供的信息，解答以下问题：
(1)、求该班学生的人数；
(2)、在图（1）中，将表示“步行”的部分补充完整；(3)、如果全年级共600名同学，请你估算全年级步行上学的学生人数？
21. 桌子上放有质地均匀，反面相同的3张卡片，正面分别标有数字1、2、3．将这些卡片反面朝上洗匀后放在桌面上，先从中任意抽出1张卡片，用卡片上所标的数字作为十位上的数字，将取出的卡片反面朝上放回洗匀；再从中任意抽取1张卡片，用卡片上所标的数字作为个位数字．试用列表或画树状图的方法分析，组成的两位数恰好能被3整除的概率是多少？
22. 如图，O为矩形ABCD对角线的交点，DE∥AC，CE∥BD．
(1)、试判断四边形OCED的形状，并说明理由；(2)、若AB=6，BC=8，求四边形OCED的面积．
23. 已知：如图，BC是⊙O的弦，线段AD经过圆心O，点A在圆上，AD⊥BC，垂足为点D，若AD=8，tanA= ．
(1)、求弦BC的长；(2)、求⊙O半径的长．24. 某公司准备投资开发A、B两种新产品，通过市场调研发现：如果单独投资A种产品，则所获利润yA（万元）与投资金额x（万元）之间满足正比例函数关系：yA=kx；如果单独投资B种产品，则所获利润yB（万元）与投资金额x（万元）之间满足二次函数关系：yB=ax2+bx．根据公司信息部的报告，yA、yB（万元）与投资金额x（万元）的部分对应值（如下表）x
1
5
yA
0.6
3
yB
2.8
10
(1)、求正比例函数和二次函数的解析式；
(2)、如果公司准备投资20万元同时开发A、B两种新产品，请你设计一个能获得最大利润的投资方案，并求出按此方案能获得的最大利润是多少万元？25. 在图1至图3中，直线MN与线段AB相交于点O，∠1=∠2=45°．
(1)、如图1，若AO=OB，请写出AO与BD的数量关系和位置关系；
(2)、将图1中的MN绕点O顺时针旋转得到图2，其中AO=OB．求证：AC=BD，AC⊥BD；
(3)、将图2中的OB拉长为AO的k倍得到图3，求 的值．
26. 如图，已知点A（﹣4，8）和点B（2，n）在抛物线y=ax2上．
(1)、求a的值及点B关于x轴对称点P的坐标，并在x轴上找一点Q，使得AQ+QB最短，求出点Q的坐标；(2)、平移抛物线y=ax2 ， 记平移后点A的对应点为A′，点B的对应点为B′，点C（﹣2，0）和点D（﹣4，0）是x轴上的两个定点．①当抛物线向左平移到某个位置时，A′C+CB′最短，求此时抛物线的函数解析式；
②当抛物线向左或向右平移时，是否存在某个位置，使四边形A′B′CD的周长最短？若存在，求出此时抛物线的函数解析式；若不存在，请说明理由．