江西省赣州市中心城区六校联盟2018届九年级下学期数学中考模拟试卷

试卷更新日期：2018-06-13 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列图形中，既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列运算中，正确的是（）．

A、 ${(a + b)}^{2} = a^{2} + b^{2}$ B、 $a^{2} \cdot a^{3} = a^{6}$ C、 $5 a - 2 a = 3$ D、 ${(a^{2})}^{3} = a^{6}$

查看试题解析
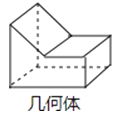
3.
如图所示为某几何体的示意图，该几何体的左视图应为（　　）

A、 B、 C、 D、

查看试题解析
4. 如图，一个含有30°角的直角三角板的两个顶点放在一个矩形的对边上，如果 $∠ 1 = 25 °$ ，那么 $∠$ 2的度数是（）

A、120° B、115° C、105° D、100°

查看试题解析
5. 已知m，n是一元二次方程x ²-4x-3=0的两个实数根，则 $(m - 2) (n - 2)$ 为（）．

A、-1 B、-3 C、-5 D、-7

查看试题解析
6. 已知抛物线 $y = a x^{2} + b x + c$ 与反比例函数 $y = \frac{b}{x}$ 的图像在第一象限有一个公共点，其横坐标为1，则一次函数 $y = b x + a c$ 的图像可能是（）

A、 B、 C、 D、

查看试题解析

二、填空题

7. 函数 $y = \frac{\sqrt{x + 1}}{x - 2}$ ，自变量 $x$ 的取值范围是．

查看试题解析
8. 分解因式：ab²﹣2ab+a= ．

查看试题解析
9. 如图，数轴上点A所表示的实数是．

查看试题解析
10. 将一副三角尺如图所示叠放在一起，则△AEB与△CED的面积比为．

查看试题解析
11. 已知圆锥如图所示放置，.其主视图面积为12，俯视图的周长为6π，则该圆锥的侧面积为.

查看试题解析
12. 已知抛物线 $y = a x^{2}$ 与线段AB无公共点，且A（-2，-1），B（-1，-2），则a的取值范围是.

查看试题解析

三、解答题

13. 计算

(1)、计算： $- 2^{2} + | \sqrt{12} - 4 | + （ \frac{1}{3} ）^{- 1} + 2 tan 60 °$

(2)、求不等式组 ${\begin{matrix} 6 - 2 x > 0 \\ 2 x \geq x - 1 \end{matrix}$ 的解集

查看试题解析
14. 如图，点C，F，E，B在一条直线上，∠CFD＝∠BEA，CE＝BF，DF＝AE，写出CD与AB之间的关系，并证明你的结论．

查看试题解析
15. 某日学校值周教师巡查早读情况，发现九年级共有三名学生迟到，年级主任通报九年级情况后，九（1）班班主任是数学老师，借此事在课堂上请同学们猜一猜、算一算迟到的学生是一个男生和两个女生的概率，李晓说：共有四种情况：一男二女，一女二男，三男，三女，因此概率是 $\frac{1}{4}$ ．请你利用树状图，判断李晓说法的正确性

查看试题解析
16. 如图，AE为菱形ABCD的高，请仅用无刻度的直尺按要求画图.（不写画法，保留画图痕迹）.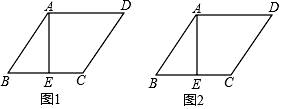

(1)、在图1中，过点C画出AB边上的高；

(2)、在图2中，过点C画出AD边上的高.

查看试题解析
17. 某商店用1050元购进第一批某种文具盒，很快卖完．又用1440元购进第二批该种文具盒，但第二批每只文具盒的进价是第一批进价的1.2倍，数量比第一批多了10只.求第一批每只文具盒的进价是多少元？

查看试题解析
18. 中学生带手机上学的现象越来越受到社会的关注，为此某记者随机调查了某市城区若干名中学生家长对这种现象的态度（态度分为：A．无所谓；B．基本赞成；C．赞成；D．反对）．并将调查结果绘制成频数折线统计图1和扇形统计图2（不完整）．请根据图中提供的信息，解答下列问题：

(1)、此次抽样调查中，共调查了多少名中学生家长；

(2)、求出图2中扇形C所对的圆心角的度数，并将图1补充完整；

(3)、根据抽样调查结果，请你估计该市城区6000名中学生家长中有多少名家长持反对态度．

查看试题解析
19. 如图是小强洗漱时的侧面示意图，洗漱台(矩形ABCD)靠墙摆放，高AD＝80cm，宽AB＝48cm，小强身高166cm，下半身FG＝100cm，洗漱时下半身与地面成80°(∠FGK＝80°)，身体前倾成125°(∠EFG＝125°)，脚与洗漱台距离GC＝15cm(点D，C，G，K在同一直线上)．

(1)、此时小强头部E点与地面DK相距多少？

(2)、小强希望他的头部E恰好在洗漱盆AB的中点O的正上方，他应向前或后退多少？
(sin80°≈0.98，cos80°≈0.17， $\sqrt{2}$ ≈1.41，结果精确到0.1cm)

查看试题解析
20. 如图，在平面直角坐标系中，Rt△AOB的斜边OA在x轴的正半轴上，∠OBA=90°，且tan∠AOB= $\frac{1}{2}$ ，OB= $2 \sqrt{5}$ ，反比例函数 $y = \frac{k}{x}$ 的图象经过点B．

(1)、求反比例函数的表达式；

(2)、若△AMB与△AOB关于直线AB对称，一次函数y=mx+n的图象过点M、A，求一次函数的表达式．

查看试题解析
21. 如图，在△ABC中，AB=AC，以AB为直径作圆O，分别交BC于点D，交CA的延长线于点E，过点D作DH⊥AC于点H，连接DE交线段OA于点F．

(1)、求证：DH是圆O的切线；

(2)、若A为EH的中点，求 $\frac{E F}{F D}$ 的值；

(3)、若EA=EF=1，求圆O的半径．

查看试题解析
22. 在平面直角坐标系中，规定：抛物线 $y = a {(x - h)}^{2} + k$ 的伴随直线为 $y = a (x - h) + k$ ．例如：抛物线 $y = 2 {(x + 1)}^{2} - 3$ 的伴随直线为 $y = 2 {(x + 1)}^{2} - 3$ ，即y=2x﹣1．

(1)、在上面规定下，抛物线 $y = {(x + 1)}^{2} - 4$ 的顶点坐标为，伴随直线为，抛物线 $y = {(x + 1)}^{2} - 4$ 与其伴随直线的交点坐标为和；

(2)、如图，顶点在第一象限的抛物线 $y = m {(x - 1)}^{2} - 4 m$ 与其伴随直线相交于点A，B（点A在点B的左侧），与x轴交于点C，D．
①若∠CAB=90°，求m的值；
②如果点P（x，y）是直线BC上方抛物线上的一个动点，△PBC的面积记为S，当S取得最大值 $\frac{27}{4}$ 时，求m的值．

查看试题解析
23. 【操作发现】
如图①，在边长为1个单位长度的小正方形组成的网格中，△ABC的三个顶点均在格点上．

(1)、请按要求画图：将△ABC绕点A按顺时针方向旋转90°，点B的对应点为B′，点C的对应点为C′，连接BB′；

(2)、在（1）所画图形中，∠AB′B= ．

(3)、【问题解决】
如图②，在等边三角形ABC中，AC=7，点P在△ABC内，且∠APC=90°，∠BPC=120°，求△APC的面积．
小明同学通过观察、分析、思考，对上述问题形成了如下想法：
想法一：将△APC绕点A按顺时针方向旋转60°，得到△AP′B，连接PP′，寻找PA，PB，PC三条线段之间的数量关系；
想法二：将△APB绕点A按逆时针方向旋转60°，得到△AP′C′，连接PP′，寻找PA，PB，PC三条线段之间的数量关系．
请参考小明同学的想法，完成该问题的解答过程．（一种方法即可）

(4)、【灵活运用】
如图③，在四边形ABCD中，AE⊥BC，垂足为E，∠BAE=∠ADC，BE=CE=2，CD=5，AD=kAB（k为常数），求BD的长（用含k的式子表示）．

查看试题解析