吉林省2018届数学中考全真模拟试卷（三）
试卷更新日期：2018-06-12 类型：中考模拟
一、单选题
-
1. ﹣2的绝对值是（ ）A、 2 B、－2 C、0 D、2. 等腰三角形有一个角是90°，则另两个角分别是（ ）
A、30°，60° B、45°，45° C、45°，90° D、20°，70°3. 下列交通标志中，是中心对称图形的是（ ）A、
B、
C、
D、
4. 在一个不透明的盒子里有2个红球和n个白球，这些球除颜色外其余完全相同，摇匀后随机摸出一个，摸到红球的概率是 ，则n的值为（ ）A、10 B、8 C、5 D、35. 如图，工人师傅在工程施工中需在同一平面内弯制一个变形管道ABCD，使其拐角∠ABC=150°，∠BCD=30°，则（ ）
A、AB∥BC B、BC∥CD C、AB∥DC D、AB与CD相交6. 已知点P（﹣1，4）在反比例函数 (k≠0)的图象上，则k的值是（ ）A、 B、 C、4 D、﹣47. 如图，A，D是⊙O上的两点，BC是直径，若∠D=35°，则∠OCA的度数是（ ）
A、35° B、55° C、65° D、70°8. 如图，不等式组 的解集在数轴上表示正确的是（ ）A、
B、
C、
D、
9. 如图是二次函数y=ax2+bx+c过点A（﹣3，0），对称轴为x=﹣1．给出四个结论：①b2＞4ac，②2a+b=0；③a﹣b+c=0；④5a＜b．其中正确结论是（ ）
A、②④ B、①④ C、②③ D、①③二、填空题
-
10. 分解因式 4x2 – 4xy + y2 = .11. 计算 的结果是 ．12. 如图，两同心圆的大圆半径长为5cm，小圆半径长为3cm，大圆的弦AB与小圆相切，切点为C，则弦AB的长是
13. 小亮与小明一起玩“石头、剪刀、布”的游戏，两同学同时出“剪刀”的概率是 ．14. 如图，在▱ABCD中，AB= ，AD=4，将▱ABCD沿AE翻折后，点B恰好与点C重合，则折痕AE的长为 ．
15. 如图，点A在双曲线y= 上，点B在双曲线y= 上，且AB∥y轴，C，D在y轴上，若四边形ABCD为平行四边形，则它的面积为 ．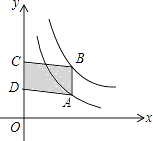
三、解答题
-
16. 计算：2sin60°+2﹣1﹣20160﹣|﹣ |17. 先化简，再求值：（1﹣ ）÷ ，其中a= +1．18. 解不等式组 ，并求它的整数解．19. 在我市实施“城乡环境综合治理”期间，某校组织学生开展“走出校门，服务社会”的公益活动．八年级一班王浩根据本班同学参加这次活动的情况，制作了如下的统计图表：
该班学生参加各项服务的频数、频率统计表：
服务类别
频数
频率
文明宣传员
4
0.08
文明劝导员
10
义务小警卫
8
0.16
环境小卫士
0.32
小小活雷锋
12
0.24
请根据上面的统计图表，解答下列问题：
(1)、该班参加这次公益活动的学生共有名；(2)、请补全频数、频率统计表和频数分布直方图；(3)、若八年级共有900名学生报名参加了这次公益活动，试估计参加文明劝导的学生人数．20. 为测山高，在点A处测得山顶D的仰角为30°，从点A向山的方向前进140米到达点B，在B处测得山顶D的仰角为60°（如图①）．
(1)、在所给的图②中尺规作图：过点D作DC⊥AB，交AB的延长线于点C（保留作图痕迹）；(2)、山高DC是多少（结果保留根号形式）？21. 随着经济收入的提高以及汽车业的快速发展，家用汽车已越来越多地进入普通家庭，汽车消费成为新亮点．抽样调查显示，截止2008年底全市汽车拥有量为14.4万辆．已知2006年底全市汽车拥有量为10万辆．(1)、求2006年底至2008年底我市汽车拥有量的年平均增长率；
(2)、为保护城市环境，要求我市到2010年底汽车拥有量不超过15.464万辆，据估计从2008年底起，此后每年报废的汽车数量是上年底汽车拥有量的10%，那么每年新增汽车数量最多不超过多少辆？（假定每年新增汽车数量相同）
22. 如图，在平面直角坐标系中，O(0，0)，A(0，－6)，B(8，0)三点在⊙P上．
(1)、求⊙P的半径及圆心P的坐标；(2)、M为劣弧 的中点，求证：AM是∠OAB的平分线；(3)、连接BM并延长交y轴于点N，求N，M点的坐标．23. 如图，在平面直角坐标系xOy中，反比例函数y = 的图象与一次函数 y =k(x -2 )的图象交点为A（3，2），B（x，y）。
(1)、求反比例函数与一次函数的解析式及B点坐标；(2)、若C是y轴上的点，且满足△ABC的面积为10，求C点坐标。
24. 如图，正方形ABCD的边长为3cm，P、Q分别从B、A出发沿BC，AD方向运动，P点的运动速度是1 cm/秒，Q点的运动速度是2 cm/秒。连接AP并过Q作QE⊥AP垂足为E。
(1)、求证：△ABP∽△QEA ；(2)、当运动时间t为何值时，△ABP≌△QEA；
(3)、设△QEA的面积为y，用运动时间t表示△QEA的面积y。（不要求考虑t的取值范围）（提示：解答（2）（3）时可不分先后）
25. 在平面直角坐标系中，已知点A（-2，0），B（2，0），C（3，5）。
(1)、求过点A、C的直线解析式和过点A、B、C的抛物线的解析式；(2)、求过点A、B及抛物线的顶点D的⊙P的圆心P的坐标；(3)、在抛物线上是否存在点Q，使AQ与⊙P相切，若存在请求出Q点坐标。