吉林省2018届数学中考全真模拟试卷(二)
试卷更新日期:2018-06-12 类型:中考模拟
一、单选题
-
1. 给出四个数0, ,π,﹣1,其中最小的是( )A、0 B、 C、π D、﹣12. 在Rt△ABC中,∠C=90°,sinA= ,则cosB的值为( )A、 B、 C、 D、3. 下列计算正确的是( )
A、x3−x2=x B、x3⋅x2=x6 C、x3÷x2=x D、(x3)2=x54. 下列不等式变形正确的是( )A、由a>b,得a﹣2<b﹣2 B、由a>b,得|a|>|b| C、由a>b,得﹣2a<﹣2b D、由a>b,得a2>b25. 如图,一个空心圆柱体,其主视图正确的是( ) A、
A、 B、
B、 C、
C、 D、
D、 6. 在一个不透明的盒子里有2个红球和n个白球,这些球除颜色外其余完全相同,摇匀后随机摸出一个,摸到红球的概率是 ,则n的值为( )A、10 B、8 C、5 D、37. 一个正多边形的内角和为540°,则这个正多边形的每一个外角等于( )A、108° B、90° C、72° D、60°8. 为了绿化校园,30名学生共种78棵树苗,其中男生每人种3棵,女生每人种2棵,设男生有x人,女生有y人,根据题意,所列方程组正确的是( )A、 B、 C、 D、9. 已知⊙O的直径AB与弦AC的夹角为35°,过C点的切线PC与AB的延长线交于点P,则∠P等于( )
6. 在一个不透明的盒子里有2个红球和n个白球,这些球除颜色外其余完全相同,摇匀后随机摸出一个,摸到红球的概率是 ,则n的值为( )A、10 B、8 C、5 D、37. 一个正多边形的内角和为540°,则这个正多边形的每一个外角等于( )A、108° B、90° C、72° D、60°8. 为了绿化校园,30名学生共种78棵树苗,其中男生每人种3棵,女生每人种2棵,设男生有x人,女生有y人,根据题意,所列方程组正确的是( )A、 B、 C、 D、9. 已知⊙O的直径AB与弦AC的夹角为35°,过C点的切线PC与AB的延长线交于点P,则∠P等于( )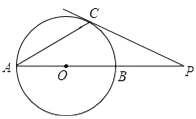 A、15° B、20° C、25° D、30°10. 已知一次函数y=kx+b的图象如图,那么正比例函数y=kx和反比例函数y= 在同一坐标系中的图象大致是( )
A、15° B、20° C、25° D、30°10. 已知一次函数y=kx+b的图象如图,那么正比例函数y=kx和反比例函数y= 在同一坐标系中的图象大致是( )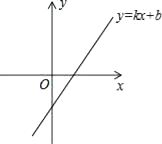 A、
A、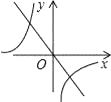 B、
B、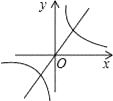 C、
C、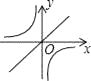 D、
D、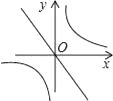
二、填空题
-
11. 若 在实数范围内有意义,则x的取值范围是 .12. 分解因式:x3﹣2x2+x= .13. 若实数a、b满足|a+2|+ =0,则 = .14. PM 2.5是指大气中直径小于或等于0.0000025m的颗粒物,将0.0000025用科学记数法表示为 .15. 如图,在△ABC中,点D,E,F分别在AB,AC,BC上,DE∥BC,EF∥AB.若AB=8,BD=3,BF=4,则FC的长为 .
 16. 如图,将一矩形纸片ABCD折叠,使两个顶点A,C重合,折痕为FG.若AB=4,BC=8,则△ABF的面积为 .
16. 如图,将一矩形纸片ABCD折叠,使两个顶点A,C重合,折痕为FG.若AB=4,BC=8,则△ABF的面积为 .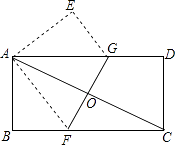 17. 如图,港口A在观测站O的正东方向,OA=40海里,某船从港口A出发,沿北偏东15°方向航行半小时后到达B处,此时从观测站O处测得该船位于北偏东60°的方向.求该船航行的速度 .
17. 如图,港口A在观测站O的正东方向,OA=40海里,某船从港口A出发,沿北偏东15°方向航行半小时后到达B处,此时从观测站O处测得该船位于北偏东60°的方向.求该船航行的速度 . 18. 如图,点A是反比例函数y= 图象上的一个动点,过点A作AB⊥x轴,AC⊥y轴,垂足分别为B,C,矩形ABOC的面积为4,则k=.
18. 如图,点A是反比例函数y= 图象上的一个动点,过点A作AB⊥x轴,AC⊥y轴,垂足分别为B,C,矩形ABOC的面积为4,则k=.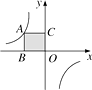
三、解答题
-
19. 计算:(﹣ )﹣2﹣|﹣1+ |+2sin60°+(π﹣4)0 .20. 先化简,再求值: ,其中x= .21. 某学校为了增强学生体质,决定开设以下体育课外活动项目:A.篮球 B.乒乓球C.羽毛球 D.足球,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:
 (1)、这次被调查的学生共有人;(2)、请你将条形统计图(2)补充完整;(3)、在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答)
(1)、这次被调查的学生共有人;(2)、请你将条形统计图(2)补充完整;(3)、在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答)
22. 已知:如图,AB与⊙O相切于点C,OA=OB,⊙O的直径为4,AB=8. (1)、求OB的长;(2)、求sinA的值.23. 如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1)、求OB的长;(2)、求sinA的值.23. 如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).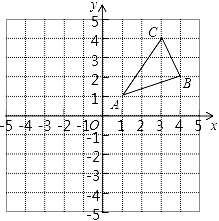
①请画出△ABC关于y轴对称的△A1B1C1;
②请画出△ABC关于x对称的△A2B2C2的各点坐标;
③在x轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出点P的坐标.
24. 现代互联网技术的广泛应用,催生了快递行业的高速发展.小明计划给朋友快递一部分物品,经了解有甲、乙两家快递公司比较合适.甲公司表示:快递物品不超过1千克的,按每千克22元收费;超过1千克,超过的部分按每千克15元收费.乙公司表示:按每千克16元收费,另加包装费3元.设小明快递物品x千克.(1)、请分别写出甲、乙两家快递公司快递该物品的费用y(元)与x(千克)之间的函数关系式;(2)、小明选择哪家快递公司更省钱?25. 如图1,在正方形ABCD中,点E,F分别是边BC,AB上的点,且CE=BF.连接DE,过点E作EG⊥DE,使EG=DE,连接FG,FC.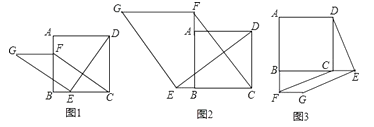 (1)、请判断:FG与CE的数量关系是 ,位置关系是;(2)、如图2,若点E,F分别是边CB,BA延长线上的点,其它条件不变,(1)中结论是否仍然成立?请作出判断并给予证明;(3)、如图3,若点E,F分别是边BC,AB延长线上的点,其它条件不变,(1)中结论是否仍然成立?请直接写出你的判断.26. 如图,抛物线y= ﹣x﹣4与坐标轴相交于A、B、C三点,P是线段AB上一动点(端点除外),过P作PD∥AC,交BC于点D,连接CP.
(1)、请判断:FG与CE的数量关系是 ,位置关系是;(2)、如图2,若点E,F分别是边CB,BA延长线上的点,其它条件不变,(1)中结论是否仍然成立?请作出判断并给予证明;(3)、如图3,若点E,F分别是边BC,AB延长线上的点,其它条件不变,(1)中结论是否仍然成立?请直接写出你的判断.26. 如图,抛物线y= ﹣x﹣4与坐标轴相交于A、B、C三点,P是线段AB上一动点(端点除外),过P作PD∥AC,交BC于点D,连接CP.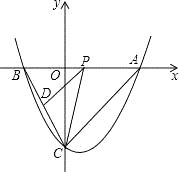 (1)、直接写出A、B、C的坐标;(2)、求抛物线y= ﹣x﹣4的对称轴和顶点坐标;(3)、求△PCD面积的最大值,并判断当△PCD的面积取最大值时,以PA、PD为邻边的平行四边形是否为菱形.
(1)、直接写出A、B、C的坐标;(2)、求抛物线y= ﹣x﹣4的对称轴和顶点坐标;(3)、求△PCD面积的最大值,并判断当△PCD的面积取最大值时,以PA、PD为邻边的平行四边形是否为菱形.