湖北省咸宁市咸安区2018届数学中考模拟试卷(3月)
试卷更新日期:2018-06-12 类型:中考模拟
一、单选题
-
1. 下列各数中,小于﹣2的数是( )
A、2 B、1 C、﹣1 D、﹣42. 下列各式计算正确的是( )A、(﹣3x3)2=9x6 B、(a﹣b)2=a2﹣b2 C、a3•a2=a6 D、x2+x2=x43. 我市某中学举办了一次以“我的中国梦”为主题的演讲比赛,最后确定7名同学参加决赛,他们的决赛成绩各不相同,其中李华已经知道自己的成绩,但能否进前四名,他还必须清楚这七名同学成绩的( )A、众数 B、平均数 C、中位数 D、方差4. 民族图案是数学文化中的一块瑰宝.下列图案中,既是中心对称图形也是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 5. 从下列不等式中选择一个与x+1≥2组成不等式组,使该不等式组的解集为x≥1,那么这个不等式可以是( )
5. 从下列不等式中选择一个与x+1≥2组成不等式组,使该不等式组的解集为x≥1,那么这个不等式可以是( )
A、x>-1 B、x>2 C、x<-1 D、x<26. 如图,有一矩形纸片ABCD,AB=6,AD=8,将纸片折叠使AB落在AD边上,折痕为AE,再将△ABE以BE为折痕向右折叠,AE与CD交于点F,则 的值是( )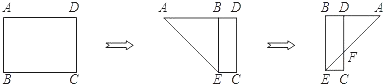 A、1 B、 C、 D、7. 已知点E(2,1)在二次函数 (m为常数)的图像上,则点E关于图像对称轴的对称点坐标是( )
A、1 B、 C、 D、7. 已知点E(2,1)在二次函数 (m为常数)的图像上,则点E关于图像对称轴的对称点坐标是( )
A、(4,1) B、(5,1) C、(6,1) D、(7,1)8. 如图,在Rt△ABC中,∠C=90°,AC=BC=6cm,点P从点A出发,沿AB方向以每秒 cm的速度向终点B运动;同时,动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动,将△PQC沿BC翻折,点P的对应点为点P′.设点Q运动的时间为t秒,若四边形QPCP′为菱形,则t的值为( )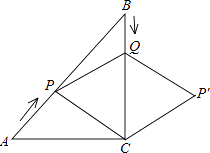 A、 B、2 C、2 D、3
A、 B、2 C、2 D、3二、填空题
-
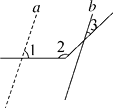
9. 我国南海海域面积为3500000km2 , 用科学记数法表示3500000为10. 如图,∠1=70°,直线a平移后得到直线b,则∠2-∠3=°.
 11. 如果实数x、y满足方程组 ,那么x2﹣y2的值为12. 如图,△ABC的顶点都在正方形网格的格点上,则tanA=
11. 如果实数x、y满足方程组 ,那么x2﹣y2的值为12. 如图,△ABC的顶点都在正方形网格的格点上,则tanA=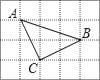 13. 某商品每件标价为150元,若按标价打8折后,再降价10元销售,仍获利10%,则该商品每件的进价为元.14. 如图,矩形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处.当△CEB′为直角三角形时,BE的长为 .
13. 某商品每件标价为150元,若按标价打8折后,再降价10元销售,仍获利10%,则该商品每件的进价为元.14. 如图,矩形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处.当△CEB′为直角三角形时,BE的长为 .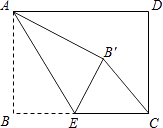 15. 如图,已知点A1 , A2 , …,An均在直线y=x﹣1上,点B1 , B2 , …,Bn均在双曲线y=﹣ 上,并且满足:A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,AnBn⊥x轴,BnAn+1⊥y轴,…,记点An的横坐标为an(n为正整数).若a1=﹣1,则a2016= .
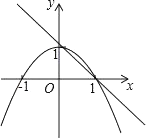
15. 如图,已知点A1 , A2 , …,An均在直线y=x﹣1上,点B1 , B2 , …,Bn均在双曲线y=﹣ 上,并且满足:A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,AnBn⊥x轴,BnAn+1⊥y轴,…,记点An的横坐标为an(n为正整数).若a1=﹣1,则a2016= .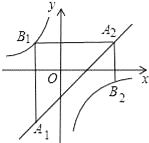 16. 如图,已知抛物线y1=﹣x2+1,直线y2=﹣x+1,当x任取一值时,x对应的函数值分别为y1 , y2 . 若y1≠y2 , 取y1 , y2中的较小值记为M;若y1=y2 , 记M=y1=y2 . 例如:当x=2时,y1=﹣3,y2=﹣1,y1<y2 , 此时M=﹣3.下列判断中:
16. 如图,已知抛物线y1=﹣x2+1,直线y2=﹣x+1,当x任取一值时,x对应的函数值分别为y1 , y2 . 若y1≠y2 , 取y1 , y2中的较小值记为M;若y1=y2 , 记M=y1=y2 . 例如:当x=2时,y1=﹣3,y2=﹣1,y1<y2 , 此时M=﹣3.下列判断中:①当x<0或x>1时,y1<y2;②当x<0时,M=y1;③使得M= 的x的值是﹣ 或 ;④对任意x的值,式子 =1﹣M总成立.
其中正确的是(填上所有正确的结论)
三、解答题
-
17.(1)、计算:( )﹣1﹣2cos30°+ +(2﹣π)0(2)、先化简,再求值: ,其中a= ﹣2.18. 一辆汽车开往距离出发地210千米的目的地,出发后第一小时内按原计划的速度匀速行驶,1小时后以原来速度的1.5倍匀速行驶,并比原计划提前40分钟到达目的地,求原计划的行驶速度.19. 某学校“体育课外活动兴趣小组”,开设了以下体育课外活动项目:A.足球 B.乒乓球C.羽毛球 D.篮球,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:
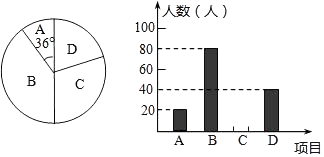 (1)、这次被调查的学生共有人,在扇形统计图中“D”对应的圆心角的度数为;(2)、请你将条形统计图补充完整;(3)、在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加市里组织的乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答).20. 如图,在平面直角坐标系中,点A、B分别在x,y轴上,点D在第一象限内,DC⊥x轴于点C,AO=CD=2,AB=DA= ,反比例函数y= (k>0)的图象过CD的中点E.
(1)、这次被调查的学生共有人,在扇形统计图中“D”对应的圆心角的度数为;(2)、请你将条形统计图补充完整;(3)、在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加市里组织的乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答).20. 如图,在平面直角坐标系中,点A、B分别在x,y轴上,点D在第一象限内,DC⊥x轴于点C,AO=CD=2,AB=DA= ,反比例函数y= (k>0)的图象过CD的中点E.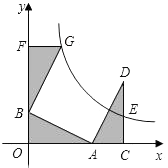 (1)、求k的值;(2)、△BFG和△DCA关于某点成中心对称,其中点F在y轴上,试判断点G是否在反比例函数的图象上,并说明理由.21. 如图,AB是⊙O的直径,CD与⊙O相切于点C,与AB的延长线交于点D,DE⊥AD且与AC的延长线交于点E.
(1)、求k的值;(2)、△BFG和△DCA关于某点成中心对称,其中点F在y轴上,试判断点G是否在反比例函数的图象上,并说明理由.21. 如图,AB是⊙O的直径,CD与⊙O相切于点C,与AB的延长线交于点D,DE⊥AD且与AC的延长线交于点E.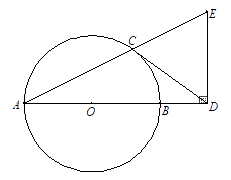 (1)、求证:DC=DE;(2)、若tan∠CAB= ,AB=3,求BD的长.
(1)、求证:DC=DE;(2)、若tan∠CAB= ,AB=3,求BD的长.
22. 如图1,为美化校园环境,某校计划在一块长为60米,宽为40米的长方形空地上修建一个长方形花圃,并将花圃四周余下的空地修建成同样宽的通道,设通道宽为a米.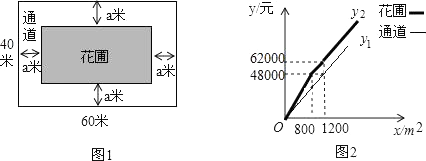 (1)、用含a的式子表示花圃的面积.(2)、如果通道所占面积是整个长方形空地面积的 ,求出此时通道的宽.(3)、已知某园林公司修建通道、花圃的造价y1(元)、y2(元)与修建面积x(m2)之间的函数关系如图2所示,如果学校决定由该公司承建此项目,并要求修建的通道的宽度不少于2米且不超过10米,那么通道宽为多少时,修建的通道和花圃的总造价最低,最低总造价为多少元?23. 我们把两条中线互相垂直的三角形称为“称为中垂三角形”,例如图1,图2,图3中,AF,BE是△ABC的中线,AF⊥BE,垂足为P,像△ABC这样的三角形均称为“中垂三角形”,设BC=a,AC=b,AB=c.
(1)、用含a的式子表示花圃的面积.(2)、如果通道所占面积是整个长方形空地面积的 ,求出此时通道的宽.(3)、已知某园林公司修建通道、花圃的造价y1(元)、y2(元)与修建面积x(m2)之间的函数关系如图2所示,如果学校决定由该公司承建此项目,并要求修建的通道的宽度不少于2米且不超过10米,那么通道宽为多少时,修建的通道和花圃的总造价最低,最低总造价为多少元?23. 我们把两条中线互相垂直的三角形称为“称为中垂三角形”,例如图1,图2,图3中,AF,BE是△ABC的中线,AF⊥BE,垂足为P,像△ABC这样的三角形均称为“中垂三角形”,设BC=a,AC=b,AB=c.特例探索
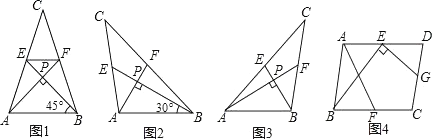 (1)、如图1,当∠ABE=45°,c=2 时,a= , b= .
(1)、如图1,当∠ABE=45°,c=2 时,a= , b= .如图2,当∠ABE=30°,c=4时,a= , b= .
归纳证明
(2)、请你观察(1)中的计算结果,猜想a2 , b2 , c2三者之间的关系,用等式表示出来,并利用图3证明你发现的关系式.拓展应用
(3)、如图4,在▱ABCD中,点E、F、G分别是AD,BC,CD的中点,BE⊥EG,AD=2 ,AB=3,求AF的长.24. 如图,在平面直角坐标系中,抛物线y=mx2﹣8mx+4m+2(m>2)与y轴的交点为A,与x轴的交点分别为B(x1 , 0),C(x2 , 0),且x2﹣x1=4,直线AD∥x轴,在x轴上有一动点E(t,0)过点E作平行于y轴的直线l与抛物线、直线AD的交点分别为P、Q.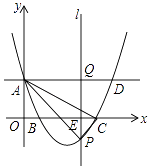 (1)、求抛物线的解析式;(2)、当0<t≤8时,求△APC面积的最大值;(3)、当t>2时,是否存在点P,使以A、P、Q为顶点的三角形与△AOB相似?若存在,求出此时t的值;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、当0<t≤8时,求△APC面积的最大值;(3)、当t>2时,是否存在点P,使以A、P、Q为顶点的三角形与△AOB相似?若存在,求出此时t的值;若不存在,请说明理由.