2018年高考理数真题试卷(全国Ⅲ卷)
试卷更新日期:2018-06-09 类型:高考真卷
一、选择题:
-
1. 已知集合 ,则 ( )A、 B、 C、 D、2. =( )A、-3-i B、-3+i C、3-i D、3+i3. 中国古建筑借助榫卯将木构件连接起来,构建的突出部分叫榫头,凹进部分叫卯眼,图中木构件右边的小长方体是榫头,若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 若 ,则 =( )
4. 若 ,则 =( )
A、 B、 C、- D、-5. 的展开式中x4的系数为( )A、10 B、20 C、40 D、806. 直线 分别与 轴, 轴交于点 两点,点 在圆 上,则 面积的取值范围是( )A、 B、 C、 D、7. 函数 的图像大致为( )A、 B、
B、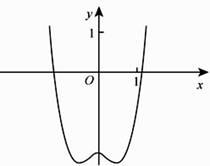 C、
C、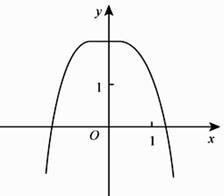 D、
D、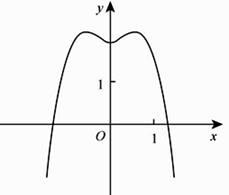 8. 某群体中的每位成员使用移动支付的概率都为 ,各成员的支付方式相互独立,设 为该群体的10位成员中使用移动支付的人数, , ,则 ( )A、0.7 B、0.6 C、0.4 D、0.39. 的内角 的对边分别为 ,若 的面积为 ,则 =( )A、 B、 C、 D、10. 设 是同一个半径为 的球的球面上四点, 为等边三角形且其面积为 ,则三棱锥 体积的最大值为( )A、 B、 C、 D、11. 设 是双曲线 ( )的左,右焦点, 是坐标原点。过 作C的一条渐近线的垂线,垂足为P。若 ,则 的离心率为( )A、 B、2 C、 D、12. 设 , ,则( )A、 B、 C、 D、
8. 某群体中的每位成员使用移动支付的概率都为 ,各成员的支付方式相互独立,设 为该群体的10位成员中使用移动支付的人数, , ,则 ( )A、0.7 B、0.6 C、0.4 D、0.39. 的内角 的对边分别为 ,若 的面积为 ,则 =( )A、 B、 C、 D、10. 设 是同一个半径为 的球的球面上四点, 为等边三角形且其面积为 ,则三棱锥 体积的最大值为( )A、 B、 C、 D、11. 设 是双曲线 ( )的左,右焦点, 是坐标原点。过 作C的一条渐近线的垂线,垂足为P。若 ,则 的离心率为( )A、 B、2 C、 D、12. 设 , ,则( )A、 B、 C、 D、二、填空题
-
13. 已知 , , ,若 ,则 。14. 曲线 在点 处的切线的斜率为 ,则 .15. 函数 在 的零点个数为 .16. 已知点 和抛物线 ,过 的焦点且斜率为 的直线与 交于 , 两点.若 ,则 .
三、解答题
-
17. 等比数列 中, .(1)、求 的通项公式;(2)、记 为 的前 项和,若Sm=63,求m。18. 某工厂为提高生产效率,开展技术创新活动,提出了完成项目生产任务的两种新的生产方式,为比较两种生产方式的效率,选取40名工人,将他们随即分成两组,每组20人,第一组工人用第一种生产方式,第二组工人用第二种生产方式,根据工人完成生产任务的工作时间(单位:min)绘制了如下茎叶图:
 (1)、根据茎叶图判断哪种生产方式的效率更高?并说明理由;(2)、求40名工人完成生产任务所需时间的中位数m,并将完成生产任务所需时间超过m和不超过m的工人数填入下面的列联表:
(1)、根据茎叶图判断哪种生产方式的效率更高?并说明理由;(2)、求40名工人完成生产任务所需时间的中位数m,并将完成生产任务所需时间超过m和不超过m的工人数填入下面的列联表:超过m
不超过m
第一种生产方式
第二种生产方式
(3)、根据2中的列联表,能否有99%的把握认为两种生产方式的效率有差异?附: ,
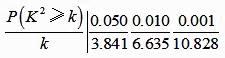 19. 如图,边长为2的正方形 所在平面与半圆弧 所在平面垂直, 是 上异于 的点。
19. 如图,边长为2的正方形 所在平面与半圆弧 所在平面垂直, 是 上异于 的点。 (1)、证明:平面 平面(2)、当三棱锥M-ABC体积最大时,求面MAB与面MCD所成二面角的正弦值。20. 已知斜率为 的直线 与椭圆 交于 两点,线段 的中点为(1)、证明:(2)、设 为 的右焦点, 为 上一点,且 ,证明: 成等差数列,并求该数列的公差。21. 已知函数 .(1)、若 ,证明:当 时, ;当 时, ;(2)、若 是 的极大值点,求a.
(1)、证明:平面 平面(2)、当三棱锥M-ABC体积最大时,求面MAB与面MCD所成二面角的正弦值。20. 已知斜率为 的直线 与椭圆 交于 两点,线段 的中点为(1)、证明:(2)、设 为 的右焦点, 为 上一点,且 ,证明: 成等差数列,并求该数列的公差。21. 已知函数 .(1)、若 ,证明:当 时, ;当 时, ;(2)、若 是 的极大值点,求a.四、选考题[选修4-4:坐标系与参数方程]