新人教版数学七年级下册 第五章相交线与平行线5.3.1《平行线的性质课时练习》
试卷更新日期:2017-01-07 类型:同步测试
一、单选题
-
1.
如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上.如果∠1=20o , 那么∠2的度数是( )
 A、30° B、25° C、20° D、15°2.
A、30° B、25° C、20° D、15°2.如图所示BC//DE,∠1=108°,∠AED=75°,则∠A的大小是( )
 A、60° B、33° C、30° D、23°3. 两条平行直线被第三条直线所截,下列命题中正确的是( )A、同位角相等,但内错角不相等 B、同位角不相等,但同旁内角互补 C、内错角相等,且同旁内角不互补 D、同位角相等,且同旁内角互补4. 一架飞机向北飞行,两次改变方向后,前进的方向与原来的航行方向平行,已知第一次向左拐50°,那么第二次向右拐( )A、40° B、50° C、130° D、150°5.
A、60° B、33° C、30° D、23°3. 两条平行直线被第三条直线所截,下列命题中正确的是( )A、同位角相等,但内错角不相等 B、同位角不相等,但同旁内角互补 C、内错角相等,且同旁内角不互补 D、同位角相等,且同旁内角互补4. 一架飞机向北飞行,两次改变方向后,前进的方向与原来的航行方向平行,已知第一次向左拐50°,那么第二次向右拐( )A、40° B、50° C、130° D、150°5.如图,下列说法正确的是( )
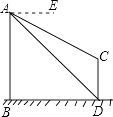
 A、若AB//CD,则∠1=∠2 B、若AD//BC,则∠B+∠BCD=180º C、若∠1=∠2,则AD//BC D、若∠3=∠4,则AD//BC6. 下列图形中,由AB//CD能得到∠1=∠2的是( )A、
A、若AB//CD,则∠1=∠2 B、若AD//BC,则∠B+∠BCD=180º C、若∠1=∠2,则AD//BC D、若∠3=∠4,则AD//BC6. 下列图形中,由AB//CD能得到∠1=∠2的是( )A、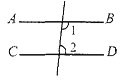 B、
B、 C、
C、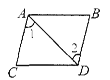 D、
D、 7. 下列语句:①两条不相交的直线叫做平行线;②过直线外一点有且只有一条直线与已知直线垂直;③若AB=BC,则点B是AC的中点;④若两角的两边互相平行,则这两个角一定相等;其中说法正确的个数是( )
7. 下列语句:①两条不相交的直线叫做平行线;②过直线外一点有且只有一条直线与已知直线垂直;③若AB=BC,则点B是AC的中点;④若两角的两边互相平行,则这两个角一定相等;其中说法正确的个数是( )
A、1 B、2 C、3 D、48. 同一平面内,两条不重合的直线的位置关系是( )A、平行或垂直 B、平行或相交 C、平行、相交或垂直 D、相交9. 下列生活实例中;①交通道口的斑马线;②天上的彩虹;③体操的纵队;④百米跑道线;⑤火车的平直铁轨线.其中属于平行线的有( )A、1个 B、2个 C、3个 D、4个10.如图,AB∥CD,∠A=46°,∠C=27°,则∠AEC的大小应为( )
 A、19° B、29° C、63° D、73°11. 如图,直线l1∥l2 , 且分别与△ABC的两边AB、AC相交,若∠A=50°,∠1=35°,∠2的度数为( )
A、19° B、29° C、63° D、73°11. 如图,直线l1∥l2 , 且分别与△ABC的两边AB、AC相交,若∠A=50°,∠1=35°,∠2的度数为( ) A、95° B、65° C、85° D、35°12.
A、95° B、65° C、85° D、35°12.如图,已知:AB∥CD,CE分别交AB、CD于点F、C,若∠E=20°,∠C=45°,则∠A的度数为( )
 A、5° B、15° C、25° D、35°13.
A、5° B、15° C、25° D、35°13.如图,l∥m,矩形ABCD的顶点B在直线m上,则∠α=( )
 A、20° B、25° C、30° D、35°14. 如图,若a∥b,则下列选项中,能直接利用“两直线平行,内错角相等”判定∠1=∠2的是( )A、
A、20° B、25° C、30° D、35°14. 如图,若a∥b,则下列选项中,能直接利用“两直线平行,内错角相等”判定∠1=∠2的是( )A、 B、
B、 C、
C、 D、
D、 15.
15.如图,如果AB∥CD,那么图中相等的内错角是( )
 A、∠1与∠5,∠2与∠6 B、∠3与∠7,∠4与∠8 C、∠5与∠1,∠4与∠8 D、∠2与∠6,∠7与∠3
A、∠1与∠5,∠2与∠6 B、∠3与∠7,∠4与∠8 C、∠5与∠1,∠4与∠8 D、∠2与∠6,∠7与∠3二、填空题
-
16.
如图,已知:∠A=∠F,∠C=∠D,求证:BD∥EC,下面是不完整的说明过程,请将过程及其依据补充完整.

证明:∵∠A=∠F(已知)
∴AC∥ ,
∴∠D=∠1
又∵∠C=∠D(已知)
∴∠1=
∴BD∥CE
17.如图,点A,C,F,B在同一直线上,CD平分∠ECB,FG∥CD.若∠ECA为α度,则∠GFB为 度(用关于α的代数式表示).
 18.
18.如图所示,一条公路两次拐弯后和原来的方向相同,即拐弯前、后的两条路平行,若第一次拐角是150°,则第二次拐角为 .
 19.
19.如图,把含有60 º角的三角尺ABC的直角顶点C放在直线DE上,当AB∥DE。则∠BCD=度。
 20.
20.如图,EF∥BC,AC平分∠BAF,∠B=80°,则∠C= °.

三、解答题
-
21.
已知:如图,AB∥EF,BC∥ED,AB,DE交于点G.
求证:∠B=∠E.
 22.
22.如图,直线a∥b,BC平分∠ABD,DE⊥BC,若∠1=70°,求∠2的度数.

四、作图题
-
23.
作图题:(只保留作图痕迹)如图,在方格纸中,有两条线段AB、BC.

利用方格纸完成以下操作:
(1)过点A作BC的平行线;
(2)过点C作AB的平行线,与(1)中的平行线交于点D;
(3)过点B作AB的垂线.
五、综合题