江苏省盐城市盐都区2018届九年级下学期数学中考一模试卷
试卷更新日期:2018-06-07 类型:中考模拟
一、单选题
-
1. 的相反数是( )A、-3 B、 C、 D、32. 下列运算正确的是( )
A、 B、 C、 D、3. 下列图形中,既是轴对称图形又是中心对称图形的是( )
A、 B、
B、 C、
C、 D、
D、 4. 在下列事件中,是必然事件的是( )A、买一张电影票,座位号一定是偶数 B、随时打开电视机,正在播新闻 C、通常情况下,抛出的篮球会下落 D、阴天就一定会下雨5. 用4个小立方块搭成如图所示的几何体,该几何体的左视图是( )
4. 在下列事件中,是必然事件的是( )A、买一张电影票,座位号一定是偶数 B、随时打开电视机,正在播新闻 C、通常情况下,抛出的篮球会下落 D、阴天就一定会下雨5. 用4个小立方块搭成如图所示的几何体,该几何体的左视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 6. 如图,a∥b,点B在直线b上,且AB⊥BC,若∠1=34°,则∠2的大小为( )
6. 如图,a∥b,点B在直线b上,且AB⊥BC,若∠1=34°,则∠2的大小为( ) A、34° B、54° C、56° D、66°7. 对于反比例函数 y= ,下列说法正确的是( )A、图像分布在第二、四象限 B、图像过点(-6,-2) C、图像与 y 轴的交点是(0,3) D、当 x<0 时,y 随 x 的增大而减小8. 如图①,在矩形 ABCD 中,动点 E 从点 A 出发,沿 AB→BC 方向运动,当点 E 到达点 C 时 停止运动.过点 E 作 FE⊥AE,交 CD 于 F 点,设点 E 运动路程为 x,FC=y,图②表示 y与 x 的函数关系的大致图像,则矩形 ABCD 的面积是( )
A、34° B、54° C、56° D、66°7. 对于反比例函数 y= ,下列说法正确的是( )A、图像分布在第二、四象限 B、图像过点(-6,-2) C、图像与 y 轴的交点是(0,3) D、当 x<0 时,y 随 x 的增大而减小8. 如图①,在矩形 ABCD 中,动点 E 从点 A 出发,沿 AB→BC 方向运动,当点 E 到达点 C 时 停止运动.过点 E 作 FE⊥AE,交 CD 于 F 点,设点 E 运动路程为 x,FC=y,图②表示 y与 x 的函数关系的大致图像,则矩形 ABCD 的面积是( )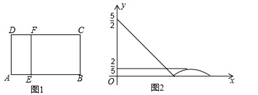 A、 B、5 C、6 D、
A、 B、5 C、6 D、二、填空题
-
9. 若二次根式 有意义,则 x 的取值范围是 .
10. 荷兰花海,风景如画,引得众多游客流连忘返.据统计今年清明小长假前往花海踏青赏花游客超过 130 000 人次,把 130 000 用科学记数法表示为 .11. 甲、乙两名同学参加“古诗词大赛”活动,五次比赛成绩的平均分都是85分,如果甲比赛成绩的方差为 =16.7,乙比赛成绩的方差为 =28.3,那么成绩比较稳定的是(填“甲”或“乙”).12. 已知二次函数y=ax2+bx+c中,自变量x与函数y的部分对应值如下表:x
…
-2
0
2
3
…
y
…
8
0
0
3
…
当x=-1时,y= .
13. 如图,在Rt△ABC中,∠C=90°,边AB的垂直平分线分别交边BC、AB于点D、E如果BC=8, ,那么BD= . 14. 如图,在▱ABCD中,E为边CD上一点,将△ADE沿AE折叠至△AD′E处,AD′与CE交于点F.若∠B=52°,∠DAE=20°,则∠FED′的大小为 .
14. 如图,在▱ABCD中,E为边CD上一点,将△ADE沿AE折叠至△AD′E处,AD′与CE交于点F.若∠B=52°,∠DAE=20°,则∠FED′的大小为 . 15. 如图,在直角坐标系中,点 A、B 的坐标分别为(4,0),(0,2),将线段 AB 向上平移 m个单位得到 A′B′,连接 OA′.如果△OA′B′是以 OB′为腰的等腰三角形,那么 m 的值为 .
15. 如图,在直角坐标系中,点 A、B 的坐标分别为(4,0),(0,2),将线段 AB 向上平移 m个单位得到 A′B′,连接 OA′.如果△OA′B′是以 OB′为腰的等腰三角形,那么 m 的值为 . 16. 如图,已知正方形 ABCD 的边长为 2,以点 A 为圆心,1 为半径作圆,点 E 是⊙A 上的任意 一点,点 E 绕点 D 按逆时针方向转转 90°,得到点 F,接 AF,则 AF 的最大值是
16. 如图,已知正方形 ABCD 的边长为 2,以点 A 为圆心,1 为半径作圆,点 E 是⊙A 上的任意 一点,点 E 绕点 D 按逆时针方向转转 90°,得到点 F,接 AF,则 AF 的最大值是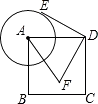
三、解答题
-
17. 计算18. 化简:
19.
20. 三张完全相同的卡片正面分别标有数字 1,3,5,将它们洗匀后,背面朝上放在桌上.
(1)、随机抽取一张,求抽到数字恰好为 3 的概率;(2)、随机抽取一张作为十位上的数字(不放回),再抽取一张作为个位上的数字,通过列表 或画树状图求所组成的两位数恰好是“51”的概率.
21. 某学校为了解本校八年级学生生物考试测试情况,随机抽取了本校八年级部分学生的生物测试成绩为样本,按A(优秀)、B(良好)、C(合格)、D(不合格)四个等级进行统计,并将统计结果绘制成如下统计图表.请你结合图表中所给信息解答下列问题:等级
人数
A(优秀)
40
B(良好)
80
C(合格)
70
D(不合格)
 (1)、请将上面表格中缺少的数据补充完整;
(1)、请将上面表格中缺少的数据补充完整;
(2)、扇形统计图中“A”部分所对应的圆心角的度数是;
(3)、该校八年级共有1200名学生参加了身体素质测试,试估计测试成绩合格以上(含合格)的人数.
22. 已知:如图,线段AB和射线BM交于点B. (1)、利用尺规完成以下作图,并保留作图痕迹(不写作法)
(1)、利用尺规完成以下作图,并保留作图痕迹(不写作法)①在射线BM上作一点C,使AC=AB;
②作∠ABM 的角平分线交AC于D点;
③在射线CM上作一点E,使CE=CD,连接DE.
(2)、在(1)所作的图形中,猜想线段BD与DE的数量关系,并证明之.
23. 某市举行长跑比赛,运动员从甲地出发跑到乙地后,又沿原路线跑回起点甲地.如图是某运 动员离开甲地的路程 s(km)与跑步时间 t(min)之间的函数关系(OA、OB 均为线段).已 知该运动员从甲地跑到乙地时的平均速度是 0.2 km/min,根据图像提供的信息,解答下列问题: (1)、a=km;(2)、组委会在距离起点甲地 3 km 处设立了一个拍摄点 P,该运动员从第一次过 P 点到第二次过 P 点所用的时间为 24 min.
(1)、a=km;(2)、组委会在距离起点甲地 3 km 处设立了一个拍摄点 P,该运动员从第一次过 P 点到第二次过 P 点所用的时间为 24 min.①求 AB 所在直线的函数表达式;
②该运动员跑完全程用时多少 min?
24. 某商场购进一批 30 瓦的 LED 灯泡和普通白炽灯泡进行销售,其进价与标价如下表:LED 灯泡
普通白炽灯泡
进价(元)
45
25
标价(元)
60
30
 (1)、该商场购进了LED灯泡与普通白炽灯泡共300个,LED灯泡按标价进行销售,而普通 白炽灯泡打九折销售,当销售完这批灯泡后可获利3200元,求该商场购进LED灯泡与 普通白炽灯泡的数量分别为多少个?
(1)、该商场购进了LED灯泡与普通白炽灯泡共300个,LED灯泡按标价进行销售,而普通 白炽灯泡打九折销售,当销售完这批灯泡后可获利3200元,求该商场购进LED灯泡与 普通白炽灯泡的数量分别为多少个?
(2)、由于春节期间热销,很快将两种灯泡销售完,若该商场计划再次购进这两种灯泡 120个,在不打折的情况下,请问如何进货,销售完这批灯泡时获利最多且不超过进货价的30%,并求出此时这批灯泡的总利润为多少元?
25. 四边形ABCD的对角线交于点 E,且AE=EC,BE=ED,以AD为直径的半圆过点E,圆心为O. (1)、如图①,求证:四边形 ABCD 为菱形;(2)、如图②,若 BC 的延长线与半圆相切于点 F,且直径 AD=6,求弧AE 的长.26. 有一边是另一边的 倍的三角形叫做智慧三角形,这两边中较长边称为智慧边,这两边的 夹角叫做智慧角.
(1)、如图①,求证:四边形 ABCD 为菱形;(2)、如图②,若 BC 的延长线与半圆相切于点 F,且直径 AD=6,求弧AE 的长.26. 有一边是另一边的 倍的三角形叫做智慧三角形,这两边中较长边称为智慧边,这两边的 夹角叫做智慧角. (1)、在 Rt△ABC 中,∠ACB=90°,若∠A 为智慧角,则∠B 的度数为;(2)、如图①,在△ABC 中,∠A=45°,∠B=30°,求证:△ABC 是智慧三角形;(3)、如图②,△ABC 是智慧三角形,BC 为智慧边,∠B 为智慧角,A(3,0),点 B,C 在函数 y= (x>0)的图像上,点 C 在点 B 的上方,且点 B 的纵坐标为 .当△ABC是直角三角形时,求 k 的值.
(1)、在 Rt△ABC 中,∠ACB=90°,若∠A 为智慧角,则∠B 的度数为;(2)、如图①,在△ABC 中,∠A=45°,∠B=30°,求证:△ABC 是智慧三角形;(3)、如图②,△ABC 是智慧三角形,BC 为智慧边,∠B 为智慧角,A(3,0),点 B,C 在函数 y= (x>0)的图像上,点 C 在点 B 的上方,且点 B 的纵坐标为 .当△ABC是直角三角形时,求 k 的值.
27. 如图①,一次函数 y= x - 2 的图像交 x 轴于点 A,交 y 轴于点 B,二次函数 y= x2 + bx + c的图像经过 A、B 两点,与 x 轴交于另一点 C. (1)、求二次函数的关系式及点 C 的坐标;(2)、如图②,若点 P 是直线 AB 上方的抛物线上一点,过点 P 作 PD∥x 轴交 AB 于点 D,PE∥y 轴交 AB 于点 E,求 PD+PE 的最大值;
(1)、求二次函数的关系式及点 C 的坐标;(2)、如图②,若点 P 是直线 AB 上方的抛物线上一点,过点 P 作 PD∥x 轴交 AB 于点 D,PE∥y 轴交 AB 于点 E,求 PD+PE 的最大值; (3)、如图③,若点 M 在抛物线的对称轴上,且∠AMB=∠ACB,求出所有满足条件的点 M的坐标.
(3)、如图③,若点 M 在抛物线的对称轴上,且∠AMB=∠ACB,求出所有满足条件的点 M的坐标.