江苏省盐城市亭湖区2018届九年级毕业班数学第一次调研测试卷
试卷更新日期:2018-06-07 类型:中考模拟
一、单选题
-
1. 下列图形中,是中心对称图形的是( )
A、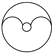 B、
B、 C、
C、 D、
D、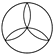 2. x取下列各数中的哪个数时,二次根式 有意义( )
2. x取下列各数中的哪个数时,二次根式 有意义( )
A、-2 B、0 C、2 D、43. 随着网络购物的兴起,截止到 年 月盐城市物流产业增加值达到 亿元,若把数 亿用科学记数法表示是( )A、 B、 C、 D、4. 苹果的单价为a元/千克,香蕉的单价为b元/千克,买2千克苹果和3千克香蕉共需( )A、(a+b)元 B、(3a+2b)元 C、(2a+3b)元 D、5(a+b)元5. 2012﹣2013NBA整个常规赛季中,科比罚球投篮的命中率大约是83.3%,下列说法错误的是( )
A、 科比罚球投篮2次,一定全部命中 B、科比罚球投篮2次,不一定全部命中 C、科比罚球投篮1次,命中的可能性较大 D、科比罚球投篮1次,不命中的可能性较小6. 设方程 的两实根分别为 、 ,且 ,则 、 满足( )
A、 B、 C、 D、二、填空题
-
7. .
8. 计算 .
9. 若 和 是同类项,则 + 的值是 .
10. 下面是甲、乙两人10次射击成绩(环数)的条形统计图,则这两人10次射击命中环数的方差 .(填“>”、“<”或“=”) 11. 分式方程 的解为x= .12. 化简 的结果是 .13. 已知反比例函数的图象经过点 和 ,则 的值是 .
11. 分式方程 的解为x= .12. 化简 的结果是 .13. 已知反比例函数的图象经过点 和 ,则 的值是 .
14. 抛物线 与 轴只有一个公共点,则 的值为 .
15. 如图,在 中, .如果将该三角形绕点 按顺时针方向旋转到 的位置,点 恰好落在边 的中点处.那么旋转的角度等于 .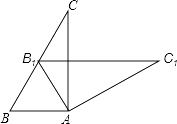
三、解答题
-
16. 计算:17. 甲、乙两人都握有分别标记为A、B、C的三张牌,两人做游戏,游戏规则是:若两人出的牌不同,则A胜B,B胜C,C胜A;若两人出的牌相同,则为平局.(1)、用树状图或列表等方法,列出甲、乙两人一次游戏的所有可能的结果;(2)、求出现平局的概率.
18. 如图 , , ,求证: .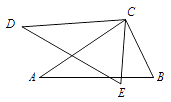 19. 已知关于 的方程 .(1)、若该方程的一个根为 ,求 的值;
19. 已知关于 的方程 .(1)、若该方程的一个根为 ,求 的值;
(2)、求证:不论 取任何实数,该方程总有两个不相等的实数根.
20. 九(1)班课题学习小组,为了了解大树生长状况,去年在学校门前点 处测得一棵大树顶点 的仰角为 ,树高 .今年他们仍在原点 处测得树顶点 的仰角为 ,问这棵树在这一年里生长了多少米?(结果保留两位小数,参考数据: , , , )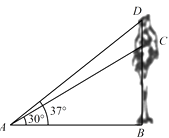 21. 某公司共25名员工,下表是他们月收入的资料.
21. 某公司共25名员工,下表是他们月收入的资料.月收入/元
45000
18000
10000
5500
4800
3400
3000
2200
人数
1
1
1
3
6
1
11
1
(1)、该公司员工月收入的中位数是元,众数是元.
(2)、根据上表,可以算得该公司员工月收入的平均数为6276元,你认为用平均数、中位数和众数中的哪一个反映该公司全体员工月收入水平较为合适?说明理由.
22. 由若干个边长为1的小正方形组成的网格,小正方形的顶点叫做格点,以格点为顶点的多边形叫格点多边形.设格点多边形的面积为S,它各边上格点的个数和为x .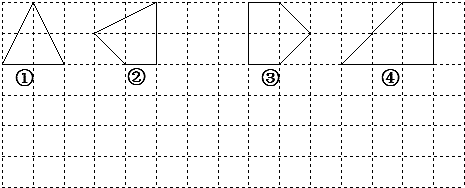 (1)、上图中的格点多边形,其内部都只有一个格点,它们的面积(S)与各边上格点的个数和(x)的对应关系如下表,请写出S与x之间的关系式.答:S= .
(1)、上图中的格点多边形,其内部都只有一个格点,它们的面积(S)与各边上格点的个数和(x)的对应关系如下表,请写出S与x之间的关系式.答:S= .多边形的序号
①
②
③
④
…
多边形的面积S
2
2.5
3
4
…
各边上格点的个数和x
4
5
6
8
…
(2)、请再画出三个边数分别为3、4、5的格点多边形,使这些多边形内部都是有且只有2个格点. 可得此类多边形的面积(S)与它各边上格点的个数和(x)之间的关系式是:S= .23. 河上有一座桥孔为抛物线形的拱桥(如图 ),水面宽 时,水面离桥孔顶部 ,因降暴雨水面上升 .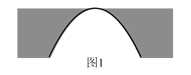
 (1)、建立适当的坐标系,并求暴雨后水面的宽;(结果保留根号)
(1)、建立适当的坐标系,并求暴雨后水面的宽;(结果保留根号)
(2)、一艘装满物资的小船,露出水面的部分高为 ,宽 (横断面如图 所示),暴雨后这艘船能从这座拱桥下通过吗?
24. 如图, 是 内一点, 与 相交于 、 两点,且与 、 分别相切于点 、 , .连接 、 . (1)、求证: .(2)、已知 , .求四边形 是矩形时 的半径.25. 为民中学租用两辆速度相同的小汽车送1名带队老师和6名学生到城区中学参加数学竞赛,每辆限坐4人(不包括司机).其中一辆小汽车在距离考场16.5 km的地方出现故障,此时离截止进考场的时刻还有50分钟,这时唯一可利用的交通工具是另一辆小汽车,且这辆车的平均速度是55 km/h,人步行的速度是5 km/h(上、下车时间忽略不计).(1)、若小汽车送4人到达考场,然后再回到出故障处接其他人,请你通过计算说明他们能否在截止进考场的时刻前到达考场;
(1)、求证: .(2)、已知 , .求四边形 是矩形时 的半径.25. 为民中学租用两辆速度相同的小汽车送1名带队老师和6名学生到城区中学参加数学竞赛,每辆限坐4人(不包括司机).其中一辆小汽车在距离考场16.5 km的地方出现故障,此时离截止进考场的时刻还有50分钟,这时唯一可利用的交通工具是另一辆小汽车,且这辆车的平均速度是55 km/h,人步行的速度是5 km/h(上、下车时间忽略不计).(1)、若小汽车送4人到达考场,然后再回到出故障处接其他人,请你通过计算说明他们能否在截止进考场的时刻前到达考场;
(2)、假如你是带队的老师,请设计一种你认为较优的运送方案,使他们能在截止进考场的时刻前到达考场,并通过计算说明方案的可行性.
26. 已知O是坐标原点,以P(1,1)为圆心的⊙P与x轴、y轴分别相切于点M和点N .
点F从点M出发,沿x轴正方向以每秒1个单位长度的速度运动,连结PF ,
过点P作PE⊥PF交y轴于点E . 设点F运动的时间是t秒(t>0). (1)、求点E的坐标(用t表示);
(1)、求点E的坐标(用t表示);
(2)、在点F运动过程中,当PF=2OE时,求t的值.
(3)、当t>1时,作点F关于点M的对称点F′.点Q是线段MF′的中点,连结QE . 在点F运动过程中,是否存在某一时刻,使得△QOE与△PMF相似,若存在,求出t的值;若不存在,请说明理由.