江苏省盐城市建湖2018届九年级数学中考一模试卷
试卷更新日期：2018-06-07 类型：中考模拟
一、单选题
-
1. 16 的平方根是（ ）
A、 6 B、-4 C、±4 D、±82. 下列图形中，既是轴对称图形又是中心对称图形的是（ ）
A、
B、
C、
D、
3. 下列运算正确的是（ ）A、4a2-2a2=2 B、a2•a4=a3 C、（a-b）2=a2-b2 D、（a+b）2=a2+2ab+b24. 正多边形的每一个内角都为 135°，则该多边形的边数为（ ）
A、5 B、6 C、7 D、85. 不等式组 的解集为 x＜2，则 k 的取值范围为（ ）
A、k＞1 B、k＜1 C、k≥1 D、k≤16. 如图，在直角坐标系中，四边形 OABC 为菱形，对角线 OB、AC 相交于 D 点，已知 A点的坐标为（10，0），双曲线 y= （ x＞0 ）经过 D 点，交 BC 的延长线于 E 点，且 OB•AC=120（OB＞AC），有下列四个结论：①双曲线的解析式为y=（x＞0）；②E 点的坐标是（4，6）；③sin∠COA= ；④EC= ；⑤AC+OB=8 ．其中正确的结论有（ ）
A、4 个 B、3 个 C、2 个 D、1 个二、填空题
-
7. 若代数式 有意义，则实数x的取值范围是 ．
8. 十八大以来，全国有 6800 多万人口摆脱贫困，以习近平同志为核心的党中央带领中国 人民创造了人类减贫史上的奇迹．把 6800 万用科学记数法表示为 ．9. 分解因式：m3-9m=.
10. 若一组数据 3，4，x，6，8 的平均数为 5，则这组数据的方差是 ．
11. 如图，△ABC中，点D在BA的延长线上，DE∥BC，如果∠BAC=80°，∠C=33°，那 么∠BDE的度数是.
12. 已知实数a在数轴上的位置如图所示，化简 的结果是 ．
13. 如图，A、B、C是⊙O上的三点，且四边形OABC是菱形．若点D是圆上异于A、B、C的另一点，则∠ADC的度数是 ．
14. “六一”前夕，市关工委准备为希望小学购进图书和文具若干套.已知 2 套文具和 3 套 图书需 104 元，3 套文具和 2 套图书需 116 元，则 1 套文具和 1 套图书需元．
15. 如图，二次函数 的图象与y轴正半轴相交，其顶点坐标为（ ，1），下列结论：①abc＞0；②a=b；③a=4c﹣4；④方程 有两个相等的实数根，其中正确的结论是 ． （只填序号即可）．
16. 如图，在平面直角坐标系中，A(4，0)、B(0，-3)，以点B为圆心、2 为半径的⊙B上 有一动点P.连接AP，若点C为AP的中点，连接OC，则OC的最小值为 ．
三、解答题
-
17. 计算：( -π)0+ cos45°+（ ）-2.18. 先化简，再求值：
，其中m满足方程m2-4m=0．
19. 已知关于 的一元二次方程 ．
(1)、求证：该方程有两个实数根；(2)、若该方程的两个实数根 、 满足 ，求 的值．
20. 某中学开展了“手机伴我健康行”主题活动，他们随机抽取部分学生进行“使用手机目的”和“每周使用手机的时间”的问卷调查，并绘制成如图①，②所示的统计图，已知“查资料”的人数是40人．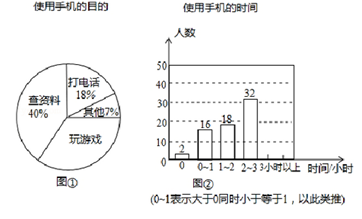
请你根据图中信息解答下列问题：
(1)、在扇形统计图中，“玩游戏”对应的圆心角度数是°；
(2)、补全条形统计图；
(3)、该校共有学生1200人，试估计每周使用手机时间在2小时以上(不含2小时)的人数.
21. 小王和小李都想去体育馆，观看在我县举行的“市长杯”青少年校园 足球联赛，但两人只有一张门票，两人想通过摸球的方式来决定谁去观看，规则如下： 在两个盒子内分别装入标有数字 1，2，3，4 的四个和标有数字 1，2，3 的三个完全相 同的小球，分别从两个盒子中各摸出一个球，如果所摸出的球上的数字之和小于 6，那 么小王去，否则就是小李去．
(1)、用树状图或列表法求出小王去的概率；
(2)、小李说：“这种规则不公平.”你认同他的说法吗？请说明理由．
22. 如图，在▱ABCD 中，∠ADB=90°，点 E 为 AB 边的中点，点 F 为CD 边的中点．
(1)、求证：四边形 DEBF 是菱形；(2)、当∠A 等于多少度时，四边形 DEBF 是正方形？并说明你的理由．23. 3月初某商品价格上涨，每件价格上涨 20%.用 3000 元买到的该商品件数比涨价前少 20 件.3 月下旬该商品开始降价，经过两次降价后，该商品价格为每 件 19.2 元．
(1)、求 3 月初该商品上涨后的价格；
(2)、若该商品两次降价率相同，求该商品价格的平均降价率．
24. 已知：如图，在△ABC 中，∠C=90°，∠BAC 的平分线 AD 交 BC于点 D，过点 D 作 DE⊥AD 交 AB 于点 E，以 AE 为直径作⊙O．
(1)、求证：BC 是⊙O 的切线；(2)、若 AC=3，BC=4，求 BE 的长．(3)、在（2）的条件中，求 cos∠EAD 的值．25. 综合题(1)、【操作发现】如图 1，△ABC 为等边三角形，点 D 为 AB 边上的一点，∠DCE=30°，将线段 CD 绕点 C 顺时针旋转 60°得到线段 CF，连接 AF、EF. 请直接 写出下列结果：
① ∠EAF的度数为；
② DE与EF之间的数量关系为；
(2)、【类比探究】如图 2，△ABC 为等腰直角三角形，∠ACB=90°，点 D 为 AB 边上的一点∠DCE=45°，将线段 CD 绕点 C 顺时针旋转 90°得到线段 CF，连接 AF、EF.
①则∠EAF的度数为；
② 线段 AE，ED，DB 之间有什么数量关系？请说明理由；
(3)、【实际应用】如图 3，△ABC 是一个三角形的余料.小张同学量得∠ACB=120°，AC=BC， 他在边 BC 上取了 D、E 两点，并量得∠BCD=15°、∠DCE=60°，这样 CD、CE 将△ABC 分成三个小三角形，请求△BCD、△DCE、△ACE 这三个三角形的面积之比.
26. 如图1，对称轴为直线x=1的抛物线y= x2+bx+c，与x轴交于A、B两点（点A在点B的左侧），且点A坐标为(-1，0).又P是抛物线上位于第一象限的点，直线AP与y轴交于点D，与抛物线对称轴交于点E，点C与坐标原点O关于该对称轴成轴对称.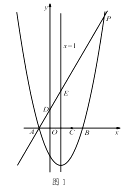
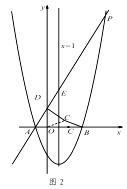(1)、求点 B 的坐标和抛物线的表达式；(2)、当 AE：EP=1：4 时，求点 E 的坐标；(3)、如图 2，在（2）的条件下，将线段 OC 绕点 O 逆时针旋转得到 OC ′，旋转角为 α(0°＜α＜90°)，连接 C ′D、C′B，求 C ′B+ C′D 的最小值．