江苏省徐州市2018届九年级数学中考一模试卷
试卷更新日期：2018-06-07 类型：中考模拟
一、单选题
-
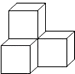
1. 下列图形中，是轴对称图形但不是中心称图形的是（ ）A、等边三角形 B、正六边形 C、正方形 D、圆2. 下列计算正确的是（ ）A、30=0 B、﹣|﹣3|=﹣3 C、3﹣1=﹣3 D、 =±33. 如图是由四个相同的小正方体组成的立体图形，它的俯视图为（ ）
A、
B、
C、
D、
4. 某同学一周中每天体育运动时间（单位：分钟）分别为：35、40、45、40、55、40、48．这组数据的众数、中位数是（ ）
A、55、40 B、40、42.5 C、40、40 D、40、455. 人体血液中，红细胞的直径约为0.000 007 7m．用科学记数法表示0.000 007 7m是（ ）A、0.77×10﹣5 B、7.7×10﹣5 C、7.7×10﹣6 D、77×10﹣76. 袋子里有4个黑球，m个白球，它们除颜色外都相同，经过大量实验，从中任取一个球恰好是白球的频率是0.20，则m的值是（ ）
A、1 B、2 C、4 D、167.如图，平行四边形ABCD中，E，F分别为AD，BC边上的一点，增加下列条件，不能得出BE∥DF的是（ ）
A、AE=CF B、BE=DF C、∠EBF=∠FDE D、∠BED=∠BFD8.如图，点A，B的坐标分别为（1，4）和（4，4），抛物线y=a（x﹣m）2+n的顶点在线段AB上运动（抛物线随顶点一起平移），与x轴交于C、D两点（C在D的左侧），点C的横坐标最小值为﹣3，则点D的横坐标最大值为（ ）
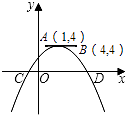A、﹣3 B、1 C、5 D、8二、填空题
-
9. 分解因式4ab2﹣9a3= ．
10. 若a2﹣2a﹣4=0，则5+4a﹣2a2= ．
11. 数轴上的两个数﹣3与a，并且a＞﹣3，它们之间的距离可以表示为 ．
12. 通过平移把点A（2，﹣3）移到点A′（4，﹣2），按同样的平移方式可将点B（﹣3，1）移到点B′，则点B′的坐标是 ．
13. 设x1、x2是方程2x2+nx+m=0的两个根，且x1+x2=4，x1x2=3．则m+n= ．
14. 如图，DE为△ABC的中位线，点F在DE上，且∠AFB=90°，若AB=6，BC=8，则EF的长为 ．
15. 点A（a，b）是函数y=x﹣1与y= 的交点，则a2b﹣ab2= ．
16. 如图，已知AB、AD是⊙O的弦，∠ABO=30°，∠ADO=20°，则∠BAD= ．
17. 已知﹣1＜b＜0，0＜a＜1，则代数式a﹣b、a+b、a+b2、a2+b中值最大的是 ．
18. 如图，在平面直角坐标系中，OA=AB，∠OAB=90°，反比例函数y= （x＞0）的图象经过A，B两点．若点A的坐标为（n，1），则k的值为 ．
三、解答题
-
19. 计算(1)、计算（﹣ ）﹣1+ ﹣（﹣ ）0(2)、计算（ ）÷20. 解答题
(1)、解不等式组：(2)、解方程：
21. 某校为更好的开展“春季趣味运动会”活动，随机在各年级抽查了部分学生，了解他们最喜爱的趣味运动项目类型（跳绳、实心球、50m、拔河共四类），并将统计结果绘制成如下不完整的频数分布表（如图所示）根据以上信息回答下列问题：
最喜爱的趣味运动项目类型频数分布表：
项目类型
频数
频率
跳绳
25
a
实心球
20
50m
b
0.4
拔河
0.15
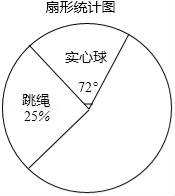(1)、直接写出a= ， b=；(2)、将图中的扇形统计图补充完整（注明项目、百分比）；(3)、若全校共有学生1200名，估计该校最喜爱50m和拔河的学生共约有多少人？22. 甲、乙、丙三人准备玩传球游戏．规则是：第1次传球从甲开始，甲先将球随机传给乙、丙两人中的一个人，再由接到球的人随机传给其他两人中的一个人…如此反复．
(1)、若传球1次，球在乙手中的概率为；(2)、若传球3次，求球在甲手中的概率（用树状图或列表法求解）．
23. 新房装修后，某居民购买家用品的清单如下表，因污水导致部分信息无法识别，根据下表解决问题：家居用品名称
单价（元）
数量（个）
金额（元）
垃圾桶
15
鞋架
40
字画
a
2
90
合计
5
185
(1)、居民购买垃圾桶，鞋架各几个？(2)、若居民再次购买字画和垃圾桶两种家居用品共花费150元，则有哪几种不同的购买方案？24. 如图，在菱形ABCF中，∠ABC=60°，延长BA至点D，延长CB至点E，使BE=AD，连结CD，EA，延长EA交CD于点G．
(1)、求证：△ACE≌△CBD；
(2)、求∠CGE的度数．
25. 某化工车间发生有害气体泄漏，自泄漏开始到完全控制利用了40min，之后将对泄漏有害气体进行清理，线段DE表示气体泄漏时车间内危险检测表显示数据y与时间x（min）之间的函数关系（0≤x≤40），反比例函数y= 对应曲线EF表示气体泄漏控制之后车间危险检测表显示数据y与时间x（min）之间的函数关系（40≤x≤？）．根据图象解答下列问题：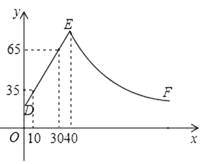
(1)、危险检测表在气体泄漏之初显示的数据是；
(2)、求反比例函数y= 的表达式，并确定车间内危险检测表恢复到气体泄漏之初数据时对应x的值．
26. 如图，在电线杆CD上的C处引拉线CE、CF固定电线杆，拉线CE和地面所成的角∠CED=60°，在离电线杆6m的B处安置高为1.5m的测角仪AB，在A处测得电线杆上C处的仰角为30°，求拉线CE的长．（结果保留根号）
27. 在Rt△ABC中，AB=BC=5，∠B=90°，将一块等腰直角三角板的直角顶点O放在斜边AC上，三角板的两直角边分别交直线AB、BC于E、F两点．
(1)、如图①，若O为AC的中点，点E、F分别在边AB、BC上．①当△OFC是等腰直角三角形时，∠FOC=；
②求证：OE=OF；
(2)、如图②，若AO：AC=1：4时，OE和OF有怎样的数量关系？证明你发现的结论．
28. 在平面直角坐标系中，抛物线y=x2+（k﹣1）x﹣k与直线y=kx+1交于A、B两点，点A在点B的左侧．
(1)、如图1，当k=1时，直接写出A，B两点的坐标；(2)、在（1）的条件下，点P为抛物线上的一个动点，且在直线AB下方，试求出△ABP面积的最大值及此时点P的坐标；
(3)、如图2，抛物线y=x2+（k﹣1）x﹣k（k＞0）与x轴交于点C、D两点（点C在点D的左侧），是否存在实数k使得直线y=kx+1与以O、C为直径的圆相切？若存在，请求出k的值；若不存在，请说明理由．