江苏省无锡市滨湖区2018届九年级数学中考一模试卷
试卷更新日期:2018-06-07 类型:中考模拟
一、单选题
-
1. 16的算术平方根是( )A、 ±4 B、±2 C、4 D、-42. 下列运算正确的是( )A、(ab)2=ab2 B、a2·a3=a6 C、(- )2=4 D、×=3. 若a<b,则下列式子中一定成立的是 ( )A、a-3<b-3 B、> C、3a>2b D、3+a>3+b4. 把多项式x2+ax+b分解因式,得(x+1)(x-3)则a , b的值分别是( )A、a=2,b=3 B、a=-2,b=-3 C、a=-2,b=3 D、a=2,b=-35. 在学校开展的“争做最优秀中学生”的一次演讲比赛中,编号1,2,3,4,5的五位同学最
后成绩如下表所示:那么这五位同学演讲成绩的众数与中位数依次是( )
参赛者编号
1
2
3
4
5
成绩/分
96
88
86
93
86
A、96,88, B、86,88, C、88,86, D、86,866. tan30°的值为( )A、 B、 C、 D、7. 将抛物线y=x2﹣4x﹣3向左平移3个单位,再向上平移5个单位,得到抛物线的表达式为( )A、y=(x+1)2﹣2 B、y=(x﹣5)2﹣2 C、y=(x﹣5)2﹣12 D、y=(x+1)2﹣128. 如图,已知BC是⊙O的直径,AB是⊙O的弦,切线AD交BC的延长线于D,若∠D=40°,则∠B的度数是( )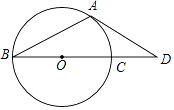 A、40° B、50° C、25° D、115°9. 如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,∠BOC=60°,顶点C的坐标为(m, ),反比例函数 的图像与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是( )
A、40° B、50° C、25° D、115°9. 如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,∠BOC=60°,顶点C的坐标为(m, ),反比例函数 的图像与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是( )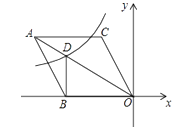 A、 B、- C、 D、-10. 如图,在△ABC中,∠ACB=90°,AB=18,cosB= ,把△ABC绕着点C旋转,使点B与AB边上的点D重合,点A落在点E处,则线段AE的长为( )
A、 B、- C、 D、-10. 如图,在△ABC中,∠ACB=90°,AB=18,cosB= ,把△ABC绕着点C旋转,使点B与AB边上的点D重合,点A落在点E处,则线段AE的长为( )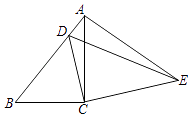 A、6 B、7 C、8 D、9
A、6 B、7 C、8 D、9二、填空题
-
11. 据媒体报道,我国因环境污染造成的巨大经济损失,每年高达860 000 000元,这个数用科学记数法表示为元.12. 函数y= 中自变量x的取值范围为 .13. 在△ABC中,已知D、E分别为边AB、AC的中点,若△ADE的周长为3cm,则△ABC的周长为 cm.14. 若圆锥底面圆的直径和母线长均为4cm,则它的侧面展开图的面积等于 cm2 .
15. 已知一个多边形的内角和与外角和之比是3:2,则这个多边形的边数为 .16. 如图,点B、E、C、F在一条直线上, AC∥DF,且AC=DF,请添加一个条件 , 使△ABC≌△DEF. 17. 如图,在正方形纸片ABCD中,EF∥AB,M,N是线段EF的两个动点,且MN= EF,若把该正方形纸片卷成一个圆柱,使点A与点B重合,若底面圆的直径为6cm,则正方形纸片上M,N两点间的距离是cm.
17. 如图,在正方形纸片ABCD中,EF∥AB,M,N是线段EF的两个动点,且MN= EF,若把该正方形纸片卷成一个圆柱,使点A与点B重合,若底面圆的直径为6cm,则正方形纸片上M,N两点间的距离是cm.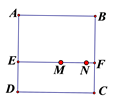 18. 如图,在△ABC中,AB=13cm,AC=12cm,BC=5cm.D是BC边上的一个动点,连接AD,过点C作CE⊥AD于E,连接BE,在点D变化的过程中,线段BE的最小值是cm.
18. 如图,在△ABC中,AB=13cm,AC=12cm,BC=5cm.D是BC边上的一个动点,连接AD,过点C作CE⊥AD于E,连接BE,在点D变化的过程中,线段BE的最小值是cm.
三、解答题
-
19. 计算与化简
(1)、 - +(1-π)0;
(2)、(x+2y)2+(x+2y) (x-2y) .20. 解答题
(1)、解方程: - =-1;(2)、解不等式组:21. 已知:如图,在平行四边形ABCD和矩形ABEF中,AC与DF相交于点G. (1)、试说明DF=CE;(2)、若AC=BF=DF,求∠ACE的度数.
(1)、试说明DF=CE;(2)、若AC=BF=DF,求∠ACE的度数.
22. 已知:如图,已知⊙O是△ABC的外接圆,AB为⊙O的直径,AC=6cm,BC=8cm. (1)、求⊙O的半径;
(1)、求⊙O的半径;
(2)、请用尺规作图作出点P,使得点P在优弧CAB上时,△PBC的面积最大,请保留作图痕迹,并求出△PBC面积的最大值.
23. “赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表.组别
成绩x分
频数(人数)
第1组
50≤x<60
6
第2组
60≤x<70
8
第3组
70≤x<80
14
第4组
80≤x<90
a
第5组
90≤x<100
10

请结合图表完成下列各题:
(1)、① 表中a的值为;② 把频数分布直方图补充完整;
(2)、若测试成绩不低于80分为优秀,则本次测试的优秀率是多少?
24. 江苏卫视《最强大脑》曾播出一期“辨脸识人”节目,参赛选手以家庭为单位,每组家庭由爸爸妈妈和宝宝3人组成,爸爸、妈妈和宝宝分散在三块区域,选手需在宝宝中选一个宝宝,然后分别在爸爸区域和妈妈区域中正确找出这个宝宝的父母,不考虑其他因素,仅从数学角度思考,已知在本期比赛中有A、B、C三组家庭进行比赛.
(1)、若机器人智能小度选择A组家庭的宝宝,求小度在妈妈区域中正确找出其妈妈的概率;
(2)、如果任选一个宝宝(假如选A组家庭),通过列表或树状图的方法,求机器人智能小度至少正确找对宝宝父母其中一人的概率.
25. 国家支持大学生创新办实业,提供小额无息贷款,学生王亮享受国家政策贷款36000元用于代理某品牌服装销售,已知该店代理的品牌服装的进价为每件40元,该品牌服装日销售量y(件)与销售价x(元/件)之间的关系可用图中的一条线段(实线)来表示.该店应支付员工的工资为每人每天82元,每天还应支付其它费用为106元(不包含贷款).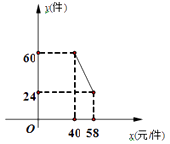 (1)、求日销售量y(件)与销售价x(元/件)之间的函数关系式;
(1)、求日销售量y(件)与销售价x(元/件)之间的函数关系式;
(2)、若该店暂不考虑偿还贷款,当某天的销售价为48元/件时,当天正好收支平衡(销售额-成本=支出),求该店员工的人数;
(3)、若该店只有2名员工,则该店至少需要多少天能还清所有贷款?此时每件服装的价格应定为多少元?
26. 已知:如图,一次函数y=-2x与二次函数y=ax2+2ax+c的图像交于A、B两点(点A在点B的右侧),与其对称轴交于点C.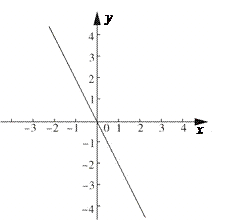 (1)、求点C的坐标;(2)、设二次函数图象的顶点为D,点C与点D 关于 x轴对称,且△ACD的面积等于2.
(1)、求点C的坐标;(2)、设二次函数图象的顶点为D,点C与点D 关于 x轴对称,且△ACD的面积等于2.① 求二次函数的解析式;
② 在该二次函数图象的对称轴上求一点P(写出其坐标),使△PBC与△ACD相似.
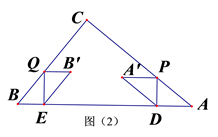
27. 如图(1),在矩形ABCD中,AB=4,BC=3,点E是射线CD上的一个动点,把△BCE沿BE折叠,点C的对应点为F, (1)、若点F刚好落在线段AD的垂直平分线上时,求线段CE的长;(2)、若点F刚好落在线段AB的垂直平分线上时,求线段CE的长;(3)、当射线AF交线段CD于点G时,请直接写出CG的最大值28. 如图(1),在△ABC中,∠C=90°,AB=5cm,BC=3cm,动点P在线段AC上以5cm/s的速度从点A运动到点C,过点P作PD⊥AB于点D,将△APD绕PD的中点旋转180°得到△A′DP,设点P的运动时间为x(s).
(1)、若点F刚好落在线段AD的垂直平分线上时,求线段CE的长;(2)、若点F刚好落在线段AB的垂直平分线上时,求线段CE的长;(3)、当射线AF交线段CD于点G时,请直接写出CG的最大值28. 如图(1),在△ABC中,∠C=90°,AB=5cm,BC=3cm,动点P在线段AC上以5cm/s的速度从点A运动到点C,过点P作PD⊥AB于点D,将△APD绕PD的中点旋转180°得到△A′DP,设点P的运动时间为x(s). (1)、当点A′落在边BC上时,求x的值;(2)、在动点P从点A运动到点C过程中,当x为何值时,△A′BC是以A′B为腰的等腰三角形;
(1)、当点A′落在边BC上时,求x的值;(2)、在动点P从点A运动到点C过程中,当x为何值时,△A′BC是以A′B为腰的等腰三角形;
(3)、如图(2),另有一动点Q与点P同时出发,在线段BC上以5cm/s的速度从点B运动到点C,过点Q作QE⊥AB于点E,将△BQE绕QE的中点旋转180°得到△B′EQ,连结A′B′,当直线A′B′与△ABC的一边垂直时,求线段A′B′的长.