江苏省苏州市2018届数学中考模拟试卷(5)
试卷更新日期:2018-06-07 类型:中考模拟
一、单选题
-
1. 下列四个数中,是负数的是( )
A、 B、 C、 D、2. 下列运算正确的是( )A、 B、 C、 D、3. 下列图形中,是中心对称图形的是( )
A、 B、
B、 C、
C、 D、
D、 4. 如图所示几何体的俯视图是( )
4. 如图所示几何体的俯视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 5. 根据下表中的信息解决问题:
5. 根据下表中的信息解决问题:
若该组数据的中位数不大于38,则符合条件的正数 的取值共有( )
A、3个 B、4个 C、5个 D、6个6. 不透明袋子中装有一个几何体模型,两位同学摸该模型并描述它的特征,甲同学:它有4个面是三角形;乙同学:它有8条棱,该模型的形状对应的立体图形可能是( )
A、三棱柱 B、四棱柱 C、三棱锥 D、四棱锥7. 如图,已知矩形 的顶点 分别落在 轴、 轴 ,则点 的坐标是( ) A、 B、 C、 D、8. 如图,已知 的四个内角的平分线分别相交于点E、F、G、H,连接 ,若 ,则 的长是( )
A、 B、 C、 D、8. 如图,已知 的四个内角的平分线分别相交于点E、F、G、H,连接 ,若 ,则 的长是( ) A、12 B、13 C、 D、9. 已知抛物线 过 , 两点,则下列关系式一定正确的( )A、 B、 C、 D、10. 如图所示,一动点从半径为2的 上的 点出发,沿着射线 方向运动到 上的点 处,再向左沿着与射线 夹角为 的方向运动到 上的点 处;接着又从 点出发,沿着射线 方向运动到 上的点 处,再向左沿着与射线 夹角为 的方向运动到 上的点 处;…按此规律运动到点A2018处,则点A2018与点 间的距离是( )
A、12 B、13 C、 D、9. 已知抛物线 过 , 两点,则下列关系式一定正确的( )A、 B、 C、 D、10. 如图所示,一动点从半径为2的 上的 点出发,沿着射线 方向运动到 上的点 处,再向左沿着与射线 夹角为 的方向运动到 上的点 处;接着又从 点出发,沿着射线 方向运动到 上的点 处,再向左沿着与射线 夹角为 的方向运动到 上的点 处;…按此规律运动到点A2018处,则点A2018与点 间的距离是( ) A、4 B、 C、 D、0
A、4 B、 C、 D、0二、填空题
-
11. 化简: = .12. 天宫二号在太空绕地球一周大约飞行42500千米,将42500用科学记数法表示为 .13. 若分式 的值为 ,则 的值等于.
14. 我们把依次连接任意一个四边形各边中点所得到的四边形叫做中点四边形.若一个四边形 的中点四边形是一个矩形,则四边形 可以是.
15. 若把代数式 化为 的形式,其中 、 为常数,则
16. 如图,四边形 内接于⊙ , 为⊙ 的直径,点 为的 中点.若 ,则 . 17. 如图,直线 经过 、 两点,则不等式 的解集为.
17. 如图,直线 经过 、 两点,则不等式 的解集为.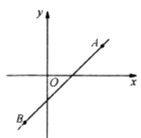 18. 如图,矩形 的顶点 在坐标原点,顶点 、 分别在 轴、 轴的正半轴上,顶点 在反比例函数 ( 为常数, )的图像上,将矩形 绕点 按逆时针方向旋转90°得到矩形 ,若点 的对应点 恰好落在此反比例函数的图象上,则 的值是.
18. 如图,矩形 的顶点 在坐标原点,顶点 、 分别在 轴、 轴的正半轴上,顶点 在反比例函数 ( 为常数, )的图像上,将矩形 绕点 按逆时针方向旋转90°得到矩形 ,若点 的对应点 恰好落在此反比例函数的图象上,则 的值是.
三、解答题
-
19. 计算:20. 解不等式组:
21. 先化简,再求值:(1﹣ )÷ ,其中x= ﹣2.22. 某批发市场批发甲、乙两种水果,根据以往经验和市场行情,预计夏季某一段时间内,甲种水果的销售利润 (万元)与进货量 (t)近似满足函数关系 ;乙种水果的销售利润 (万元)与进货量 (t)近似满足函数关系 (其中 , 、 为常数),且进货量 为1t时,销售利润 为1. 4万元;进货量 为2t时,销售利润 为2. 6万元.
(1)、求 (万元)与 (t)之间的函数关系式;
(2)、如果市场准备进甲、乙两种水果共10t,设乙种水果的进货量为 (t),请你写出这两种水果所获得的销售利润之和 (万元)与 (t)之间的函数关系式.并求出这两种水果各进多少吨时获得的销售利润之和最大,最大利润是多少.
23. 某数学学习网站为吸引更多人注册加入,举行了一个为期5天的推广活动.在活动期间,加入该网站的人数变化情况如下表所示: (1)、表格中 , ;(2)、请把下面的条形统计图补充完整;
(1)、表格中 , ;(2)、请把下面的条形统计图补充完整; (3)、根据以上信息,下列说法正确的是(只要填写正确说法前的序号).
(3)、根据以上信息,下列说法正确的是(只要填写正确说法前的序号).①在活动之前,该网站已有3 200人加入;
②在活动期间,每天新加入人数逐天递增;
③在活动期间,该网站新加入的总人数为2 528人.
24. 在3×3的方格纸中,点A、B、C、D、E、F分别位于如图所示的小正方形的顶点上.
(1)、从A、D、E、F四个点中任意取一点,以所取的这一点及点B、C为顶点画三角形,则所画三角形是等腰三角形的概率是;(2)、从A、D、E、F四个点中先后任意取两个不同的点,以所取的这两点及点B、C为顶点画四边形,求所画四边形是平行四边形的概率。(用树状图或列表法求解).
25. 如图,菱形 的边长为2,对角线 , 、 分别是 、 上的两个动点,且满足 . (1)、求证: ;(2)、判断 的形状,并说明理由,同时指出 是由 经过如何变换得到.26. 在平面直角坐标系 中,已知 和 的顶点坐标分别为 、 、 、 、 、 .
(1)、求证: ;(2)、判断 的形状,并说明理由,同时指出 是由 经过如何变换得到.26. 在平面直角坐标系 中,已知 和 的顶点坐标分别为 、 、 、 、 、 .按下列要求画图:以点 为位似中心,将 向 轴左侧按比例尺 放大得 的位似图形 ,并解决下列问题:
(1)、顶点 的坐标为 , 的坐标为 , 的坐标为;(2)、请你利用旋转、平移两种变换,使 通过变换后得到 ,且 恰与 拼接成一个平行四边形 (非正方形).写出符合要求的变换过程. 27. 如图,湿地景区岸边有三个观景台 、 、 .已知 m, m,点 位于点 的南偏西60. 7°方向,点 位于点 的南偏东66. 1°方向.
27. 如图,湿地景区岸边有三个观景台 、 、 .已知 m, m,点 位于点 的南偏西60. 7°方向,点 位于点 的南偏东66. 1°方向. (1)、求 的面积;(2)、景区规划在线段 的中点 处修建一个湖心亭,并修建观景栈道 .试求 、 间的距离.(结果精确到0. 1 m,参考数据: , , , , , , )28. 如图, 内接于⊙ , , 的平分线 与⊙ 交于点 ,与 交于点 ,延长 ,与 的延长线交于点 ,连接 , 是 的中点,连接 .
(1)、求 的面积;(2)、景区规划在线段 的中点 处修建一个湖心亭,并修建观景栈道 .试求 、 间的距离.(结果精确到0. 1 m,参考数据: , , , , , , )28. 如图, 内接于⊙ , , 的平分线 与⊙ 交于点 ,与 交于点 ,延长 ,与 的延长线交于点 ,连接 , 是 的中点,连接 . (1)、判断 与 的位置关系,写出你的结论并证明;(2)、求证: ;(3)、若 ,求⊙ 的面积.29. 在平面直角坐标系 中,点 、 的横坐标分别为 、 ,二次函数 的图像经过点 、 ,且 满足 ( 为常数).
(1)、判断 与 的位置关系,写出你的结论并证明;(2)、求证: ;(3)、若 ,求⊙ 的面积.29. 在平面直角坐标系 中,点 、 的横坐标分别为 、 ,二次函数 的图像经过点 、 ,且 满足 ( 为常数).
(1)、若一次函数 的图像经过 、 两点.①当 、 时,求 的值;
②若 随 的增大而减小,求 的取值范围.
(2)、当 且 、 时,判断直线 与 轴的位置关系,并说明理由;(3)、点 、 的位置随着 的变化而变化,设点 、 运动的路线与 轴分别相交于点 、 ,线段 的长度会发生变化吗?如果不变,求出 的长;如果变化,请说明理由.