广东省深圳市南山区2018届数学中考一模试卷
试卷更新日期:2018-06-07 类型:中考模拟
一、单选题
-
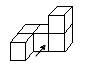
1. 下列各数中,最小的数是( )A、﹣1 B、﹣ C、0 D、12. 如图所示的几何体是由五个小正方体组合而成的,箭头所指示的为主视方向,则它的俯视图是( )
 A、
A、 B、
B、 C、
C、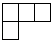 D、
D、 3. 下列图形既是轴对称图形,又是中心对称图形的是( )A、
3. 下列图形既是轴对称图形,又是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 4. 地球绕太阳公转的速度约为110000km/h,则110000用科学记数法可表示为( )A、0.11×106 B、1.1×105 C、0.11×105 D、1.1×1065. 如图,已知a∥b,∠1=120°,∠2=90°,则∠3的度数是( )
4. 地球绕太阳公转的速度约为110000km/h,则110000用科学记数法可表示为( )A、0.11×106 B、1.1×105 C、0.11×105 D、1.1×1065. 如图,已知a∥b,∠1=120°,∠2=90°,则∠3的度数是( )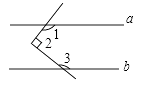 A、120° B、130° C、140° D、150°6. 下列运算正确的是( )A、5a2+3a2=8a4 B、a3•a4=a12 C、(a+2b)2=a2+4b2 D、(a-b)(-a-b)=b2-a27. 十九大以来,中央把扶贫开发工作纳入“四个全面”战略并着力持续推进,据统计2015年的某省贫困人口约484万,截止2017年底,全省贫困人口约210万,设过两年全省贫困人口的年平均下降率为x,则下列方程正确的是( )A、484(1﹣2x)=210 B、484x2=210 C、484(1﹣x)2=210 D、484(1﹣x)+484(1﹣x)2=2108. 如图,在平面直角坐标系中,点P是反比例函数y= (x>0)图象上一点,过点P作垂线,与x轴交于点Q,直线PQ交反比例函数y= (k≠0)于点M.若PQ=4MQ,则k的值为( )
A、120° B、130° C、140° D、150°6. 下列运算正确的是( )A、5a2+3a2=8a4 B、a3•a4=a12 C、(a+2b)2=a2+4b2 D、(a-b)(-a-b)=b2-a27. 十九大以来,中央把扶贫开发工作纳入“四个全面”战略并着力持续推进,据统计2015年的某省贫困人口约484万,截止2017年底,全省贫困人口约210万,设过两年全省贫困人口的年平均下降率为x,则下列方程正确的是( )A、484(1﹣2x)=210 B、484x2=210 C、484(1﹣x)2=210 D、484(1﹣x)+484(1﹣x)2=2108. 如图,在平面直角坐标系中,点P是反比例函数y= (x>0)图象上一点,过点P作垂线,与x轴交于点Q,直线PQ交反比例函数y= (k≠0)于点M.若PQ=4MQ,则k的值为( ) A、±2 B、 C、- D、±9. 如图,小桥用黑白棋子组成的一组图案,第1个图案由1个黑子组成,第2个图案由1个黑子和6个白子组成,第3个图案由13个黑子和6个白子组成,按照这样的规律排列下去,则第8个图案中共有( )和黑子.
A、±2 B、 C、- D、±9. 如图,小桥用黑白棋子组成的一组图案,第1个图案由1个黑子组成,第2个图案由1个黑子和6个白子组成,第3个图案由13个黑子和6个白子组成,按照这样的规律排列下去,则第8个图案中共有( )和黑子.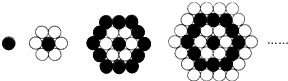 A、37 B、42 C、73 D、12110. 二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(﹣1,0),对称轴为直线x=2,下列结论①abc>0;②4a+b=0;③9a+c>3b;④当x>﹣1时,y的值随x值的增大而增大,其中正确的结论有( )
A、37 B、42 C、73 D、12110. 二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(﹣1,0),对称轴为直线x=2,下列结论①abc>0;②4a+b=0;③9a+c>3b;④当x>﹣1时,y的值随x值的增大而增大,其中正确的结论有( )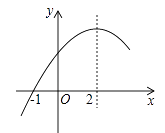 A、1个 B、2个 C、3个 D、4个11. 如图,河流的两岸PQ,MN互相平行,河岸PQ上有一排小树,已知相邻两树CD之间的距离为50米,某人在河岸MN的A处测得∠DAN=45°,然后沿河岸走了130米到达B处,测得∠CBN=60°.则河流的宽度CE为( )
A、1个 B、2个 C、3个 D、4个11. 如图,河流的两岸PQ,MN互相平行,河岸PQ上有一排小树,已知相邻两树CD之间的距离为50米,某人在河岸MN的A处测得∠DAN=45°,然后沿河岸走了130米到达B处,测得∠CBN=60°.则河流的宽度CE为( ) A、80 B、40(3﹣ ) C、40(3+ ) D、4012. 若a使关于x的不等式组 至少有三个整数解,且关于x的分式方程 + =2有正整数解,a可能是( )A、﹣3 B、3 C、5 D、8
A、80 B、40(3﹣ ) C、40(3+ ) D、4012. 若a使关于x的不等式组 至少有三个整数解,且关于x的分式方程 + =2有正整数解,a可能是( )A、﹣3 B、3 C、5 D、8二、填空题
-
13. 因式分解:y3﹣4x2y= .14. 一个不透明的盒子中装有6个红球,3个黄球和1个绿球,这些球除了颜色外无其他差别,从中随机摸出一个小球,则摸到的不是红球的概率为
15. 定义新运算:对于任意有理数a、b都有a⊗b=a(a﹣b)+1,等式右边是通常的加法、减法及乘法运算.比如:2⊗5=2×(2﹣5)+1=2×(3)+1=6+1=5.则4⊗x=13,则x= .16. 正方形ABCD中,F是AB上一点,H是BC延长线上一点,连接FH,将△FBH沿FH翻折,使点B的对应点E落在AD上,EH与CD交于点G,连接BG交FH于点M,当GB平分∠CGE时,BM=2 ,AE=8,则ED= .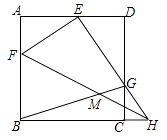
三、解答题
-
17. ( )﹣2﹣4+ +(3.14﹣x)0×cos60°.18. 先化简,再求值: ÷( +1﹣x),其中x=2.19. “共享单车,绿色出行”,现如今骑共享单车出行不但成为一种时尚,也称为共享经济的一种新形态,某校九(1)班同学在街头随机调查了一些骑共享单车出行的市民,并将他们对各种品牌单车的选择情况绘制成如下两个不完整的统计图(A:摩拜单车;B:ofo单车;C:HelloBike).请根据图中提供的信息,解答下列问题:
 (1)、求出本次参与调查的市民人数;
(1)、求出本次参与调查的市民人数;
(2)、将上面的条形图补充完整;(3)、若某区有10000名市民骑共享单车出行,根据调查数据估计该区有多少名市民选择骑摩拜单车出行?
20. 随着互联网的普及,某手机厂商采用先网络预定,然后根据订单量生产手机的方式销售,2015年该厂商将推出一款新手机,根据相关统计数据预测,定价为2200元,日预订量为20000台,若定价每减少100元,则日预订量增加10000台.
(1)、设定价减少x元,预订量为y台,写出y与x的函数关系式;
(2)、若每台手机的成本是1200元,求所获的利润w(元)与x(元)的函数关系式,并说明当定价为多少时所获利润最大;(3)、若手机加工厂每天最多加工50000台,且每批手机会有5%的故障率,通过计算说明每天最多接受的预订量为多少?按最大量接受预订时,每台售价多少元?
21. 如图.在△ABC中,BA=BC,以AB为直径的⊙O分别交AC,BC于点D、E,BC的延长线与⊙O的切线AF交于点F.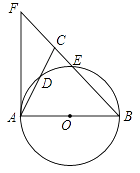 (1)、求证:∠ABC=2∠CAF;(2)、已知AC=2 ,EB=4CE,求⊙O的直径.22. 如图1,在等腰Rt△ABC中,∠BAC=90°,点E在AC上(且不与点A、C重合).在△ABC的外部作等腰Rt△CED,使∠CED=90°,连接AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF.
(1)、求证:∠ABC=2∠CAF;(2)、已知AC=2 ,EB=4CE,求⊙O的直径.22. 如图1,在等腰Rt△ABC中,∠BAC=90°,点E在AC上(且不与点A、C重合).在△ABC的外部作等腰Rt△CED,使∠CED=90°,连接AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF. (1)、求证:△AEF是等腰直角三角形;(2)、如图2,将△CED绕点C逆时针旋转,当点E在线段BC上时,连接AE,求证:AF= AE;(3)、如图3,
(1)、求证:△AEF是等腰直角三角形;(2)、如图2,将△CED绕点C逆时针旋转,当点E在线段BC上时,连接AE,求证:AF= AE;(3)、如图3,
将△CED绕点C继续逆时针旋转,当平行四边形ABFD为菱形,且△CED在△ABC的下方时,若AB=2 ,CE=2,求线段AE的长.
23. 如图1,二次函数y=ax2+bx的图象过点A(﹣1,3),顶点B的横坐标为1.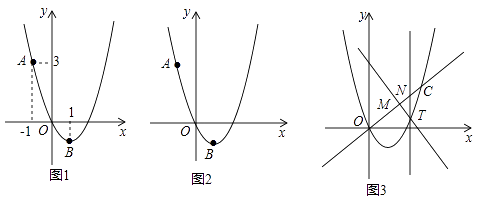 (1)、求这个二次函数的表达式;(2)、点P在该二次函数的图象上,点Q在x轴上,若以A、B、P、Q为顶点的四边形是平行四边形,求点P的坐标;(3)、如图3,一次函数y=kx(k>0)的图象与该二次函数的图象交于O、C两点,点T为该二次函数图象上位于直线OC下方的动点,过点T作直线TM⊥OC,垂足为点M,且M在线段OC上(不与O、C重合),过点T作直线TN∥y轴交OC于点N.若在点T运动的过程中, 为常数,试确定k的值.
(1)、求这个二次函数的表达式;(2)、点P在该二次函数的图象上,点Q在x轴上,若以A、B、P、Q为顶点的四边形是平行四边形,求点P的坐标;(3)、如图3,一次函数y=kx(k>0)的图象与该二次函数的图象交于O、C两点,点T为该二次函数图象上位于直线OC下方的动点,过点T作直线TM⊥OC,垂足为点M,且M在线段OC上(不与O、C重合),过点T作直线TN∥y轴交OC于点N.若在点T运动的过程中, 为常数,试确定k的值.