浙江省嘉兴市秀洲2018届数学初中毕业生学业考试适应性试卷(二)
试卷更新日期:2018-06-07 类型:中考模拟
一、选择题
-
1. 2018的相反数是( )
A、 B、 C、2018 D、-20182. 下列是手机中部分软件的图标,其中属于轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 3. 根据嘉兴市统计局的人口统计,截至2017年末,嘉兴全市常住人口约为4656000人,“4656000用科学记数法可表示为( )
3. 根据嘉兴市统计局的人口统计,截至2017年末,嘉兴全市常住人口约为4656000人,“4656000用科学记数法可表示为( )
A、4.656×105 B、46.56×105 C、4.656×106 D、0.4656×1074. 某个不等式的解集在数轴上如图所示,这个不等式可以是( ) A、2x-1≤3 B、2x-1<3 C、2x-1≥3 D、2x-1>35. 在学校开展的“美德少年”评选活动中,编号1,2,3,4,5的五位同学的最终成绩
A、2x-1≤3 B、2x-1<3 C、2x-1≥3 D、2x-1>35. 在学校开展的“美德少年”评选活动中,编号1,2,3,4,5的五位同学的最终成绩如下表所示:
参赛者编号
1
2
3
4
5
成绩/分
93
88
90
91
90
这五位同学最终成绩的众数和中位数依次是( )
A、88,90 B、90,90 C、91,90 D、90,916. 下列命题是假命题的是( )A、三角形的内心到这个三角形三边的距离相等 B、有一个内角为60°的等腰三角形是等边三角形 C、直角坐标系中,点(a,b)关于原点成中心对称的点的坐标为(-b,-a) D、有三个角是直角且一组邻边相等的四边形是正方形7. 在《九章算术》“勾股”章里有求方程x2+34x-71000=0的正根才能解答的题目。下面方程用配方法变形正确的是( )
A、(x+17)2=70711 B、(x+17)2=71289 C、(x-17)2=70711 D、(x-17)2=712898. 某品牌婴儿罐装奶粉圆形桶口如图所示,它的内直径(⊙O直径)为10cm,弧AB的度数约为90°,则弓形铁片ACB(阴影部分)的面积约为( )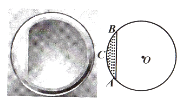 A、 B、 C、 D、9. 如图,△ABC中,D,E分别为AB,AC的中点,CD⊥BE于点F.当AB=8,AC=6时,BC的长度为( )
A、 B、 C、 D、9. 如图,△ABC中,D,E分别为AB,AC的中点,CD⊥BE于点F.当AB=8,AC=6时,BC的长度为( )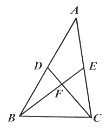 A、4 B、 C、 D、510. 如图,平面直角坐标系中,抛物线 交x轴于点B,C,交y轴于点A,点P(x,y)是抛物线上的一个动点,连接PA,AC,PC,记△ACP面积为S.当y≤3时,S随x变化的图象大致是( )
A、4 B、 C、 D、510. 如图,平面直角坐标系中,抛物线 交x轴于点B,C,交y轴于点A,点P(x,y)是抛物线上的一个动点,连接PA,AC,PC,记△ACP面积为S.当y≤3时,S随x变化的图象大致是( )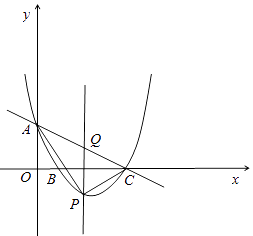 A、
A、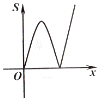 B、
B、 C、
C、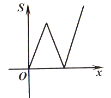 D、
D、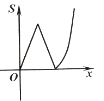
二、填空题
-
11. 9的算术平方根为 .12. 分解因式:a3-4a= .
13. 在长度为3,6,8,10的四条线段中,任意选择一条线段,使它与已知线段4和7能组成三角形的概率为 .
14. 平面直角坐标系中,菱形AOBC的位置如图所示,点A在x轴负半轴上,B(1, ),反比例函数 在第二象限的图像经过点C,则k=。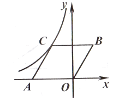 15. 农贸市场拟建两间长方形储藏室,储藏室的一面靠墙(墙长30m),中间用一面墙隔开,如图所示,已知建筑材料可建墙的长度为42m,则这两间长方形储藏室的总占地面积的最大值为m2 .
15. 农贸市场拟建两间长方形储藏室,储藏室的一面靠墙(墙长30m),中间用一面墙隔开,如图所示,已知建筑材料可建墙的长度为42m,则这两间长方形储藏室的总占地面积的最大值为m2 .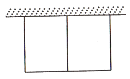 16. 如图,AB为半圆O的直径,AB=2,C,D为半圆上两个动点(D在C右侧),且满足∠COD=60°,连结AD,BC相交于点P若点C从A出发按顺时针方向运动,当点D与B重合时运动停止,则点P所经过的路径长为 .
16. 如图,AB为半圆O的直径,AB=2,C,D为半圆上两个动点(D在C右侧),且满足∠COD=60°,连结AD,BC相交于点P若点C从A出发按顺时针方向运动,当点D与B重合时运动停止,则点P所经过的路径长为 .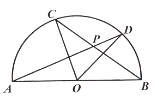
三、解答题
-
17.
(1)、计算:(2)、化简:m(m+4)+(m-2)218. 解方程:小嘉同学的解题过程如下:
将方程两边同乘以(x+1),
得:x=1+1-x
所以,x=1.
判断小嘉同学的解题过程是否正确,若不正确,请给出正确的解题过程。
19. 已知:如图,Rt△ABC中,∠ACB=90° (1)、用直尺和圆规作∠ABC的平分线,交AC于点O;(2)、在(1)的条件下,若BC=3,AC=4,求点O到AB的距离。20. 为深化课改,落实立德树人目标,某学校设置了以下四门拓展性课程:A.数学思维,B.文学鉴赏,C.红船课程,D.3D打印,规定每位学生选报一门.为了解学生的报名情况,随机抽取了部分学生进行调查,并制作成如下两幅不完整的统计图,请回答下列问题:
(1)、用直尺和圆规作∠ABC的平分线,交AC于点O;(2)、在(1)的条件下,若BC=3,AC=4,求点O到AB的距离。20. 为深化课改,落实立德树人目标,某学校设置了以下四门拓展性课程:A.数学思维,B.文学鉴赏,C.红船课程,D.3D打印,规定每位学生选报一门.为了解学生的报名情况,随机抽取了部分学生进行调查,并制作成如下两幅不完整的统计图,请回答下列问题: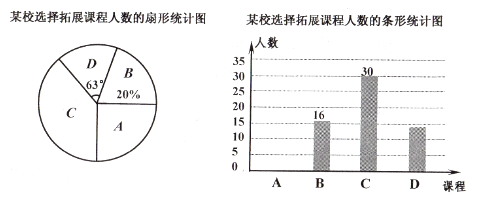 (1)、求这次被调查的学生人数;(2)、请将条形统计图补充完整;(3)、假如全校有学生1000人,请估计选报“红船课程”的学生人数。21. 为营造“安全出行”的良好交通氛围,实时监控道路交迸,某市交管部门在路口安装的高清摄像头如图所示,立杆MA与地面AB垂直,斜拉杆CD与AM交于点C,横杆DE∥AB,摄像头EF⊥DE于点E,AC=55米,CD=3米,EF=0.4米,∠CDE=162°。
(1)、求这次被调查的学生人数;(2)、请将条形统计图补充完整;(3)、假如全校有学生1000人,请估计选报“红船课程”的学生人数。21. 为营造“安全出行”的良好交通氛围,实时监控道路交迸,某市交管部门在路口安装的高清摄像头如图所示,立杆MA与地面AB垂直,斜拉杆CD与AM交于点C,横杆DE∥AB,摄像头EF⊥DE于点E,AC=55米,CD=3米,EF=0.4米,∠CDE=162°。 (1)、求∠MCD的度数;(2)、求摄像头下端点F到地面AB的距离。(精确到百分位)
(1)、求∠MCD的度数;(2)、求摄像头下端点F到地面AB的距离。(精确到百分位)(参考数据:sin72°=0.95,cos72°≈0.31,tan72°=3.08,sin18°≈0.31,cos18°≈0.95,tan18°≈0.32)
22. 购物广场内甲、乙两家商店对A,B两种商品均有优惠促销活动;甲商店的促销方案是:A商品打八折,B商品打七五折;
乙商店的促销方案是:购买一件A商品,赠送一件B商品,多买多送。
请你结合小明和小华的对话,解答下列问题:
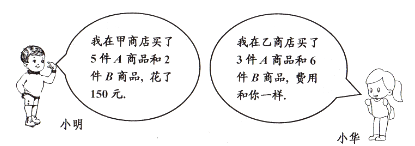 (1)、求A,B两种商品促销前的单价;(2)、假设在同一家商店购买A,B两种商品共100件,且A不超过50件,请说明选择哪家商店购买更合算。23. 我们把有两条边和其中一边的对角对应相等的两个三角形叫做友好三角形。如图,在△ABC和△ABD中,AB=AB,AD=AC,∠ABC=∠ABD,则△ABC和△ABD是友好三角形。
(1)、求A,B两种商品促销前的单价;(2)、假设在同一家商店购买A,B两种商品共100件,且A不超过50件,请说明选择哪家商店购买更合算。23. 我们把有两条边和其中一边的对角对应相等的两个三角形叫做友好三角形。如图,在△ABC和△ABD中,AB=AB,AD=AC,∠ABC=∠ABD,则△ABC和△ABD是友好三角形。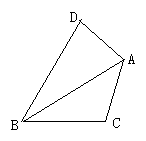
(1)、如图1,已知AD=AC,请写出图中的友好三角形;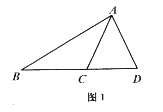
(2)、如图2,在△ABC和△ABD中,AD=AC,∠BDA=∠BCA,且∠BDA>90°,求证:△ABC≌△ABD;
(3)、如图3,△ABC内接于圆,∠ABC=30°,∠BAC=45°,BC=4。D是圆上一点,若△ABD和△ABC是友好三角形,且BD<AD,求AD的长。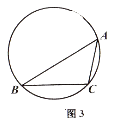
24. 如图,平面直角坐标系xOy中,抛物线y=a(x+1)(x-9)经过A,B两点,四边形OABC矩形,已知点A坐标为(0,6)。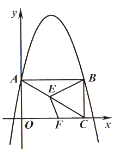 (1)、求抛物线解析式;(2)、点E在线段AC上移动(不与C重合),过点E作EF⊥BE,交x轴于点F.请判断 的值是否变化;若不变,求出它的值;若变化,请说明理由。(3)、在(2)的条件下,若E在直线AC上移动,当点E关于直线BF的对称点E在抛物线对称轴上时,请求出BE的长度。
(1)、求抛物线解析式;(2)、点E在线段AC上移动(不与C重合),过点E作EF⊥BE,交x轴于点F.请判断 的值是否变化;若不变,求出它的值;若变化,请说明理由。(3)、在(2)的条件下,若E在直线AC上移动,当点E关于直线BF的对称点E在抛物线对称轴上时,请求出BE的长度。