浙江省嘉兴市2018届数学初中毕业生学业考试适应性试卷(二)
试卷更新日期:2018-06-07 类型:中考模拟
一、选择题
-
1. 3的相反数是( )A、 B、 C、 D、32. 下列电视台图标中,属于中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 资料显示,2018届全国普通高校毕业生预计820万人,用科学记数法表示820万。这个数为( )
3. 资料显示,2018届全国普通高校毕业生预计820万人,用科学记数法表示820万。这个数为( )
A、82.0×105 B、8.2×105 C、8.2×106 D、8.2×1074. 如图是由五个相同的小正方体搭成的几何体,它的俯视图是( )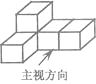 A、
A、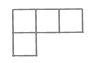 B、
B、 C、
C、 D、
D、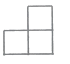 5. 著名篮球运动员科比·布莱恩特通过不断练习罚球以提高其罚球命中率,下表是科比某次训练时的进球情况.其中说法正确的是( )
5. 著名篮球运动员科比·布莱恩特通过不断练习罚球以提高其罚球命中率,下表是科比某次训练时的进球情况.其中说法正确的是( )罚篮数/次
100
200
500
800
进球数/次
90
178
453
721
A、科比每罚10个球,一定有9个球进 B、科比罚球前9个进,第10个一定不进 C、科比某场比赛中的罚球命中率一定为90% D、科比某场比赛中罚球命中率可能为100%6. 若x>y,则下列式子中错误的是( )
A、x-3>y-3 B、x+3>y+3 C、-3x>-3y D、 >7. 如图,直线 ∥ ,以直线 上的点A为圆心.适当长为半径画弧,分别交直线 , 于点B,C,连接AB,BC.那么∠1=40°,则∠ABC=( )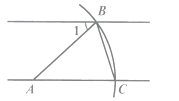 A、40° B、50° C、70° D、80°8. 一元二次方程 根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、没有实数根9. 如图,在正方形ABCD中,AD=6,点E是边CD上的动点(点E不与端点C,D重合),AE的垂直平分线FG分别交AD,AE,BC于点F,H,G.当 时,DE的长为( )
A、40° B、50° C、70° D、80°8. 一元二次方程 根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、没有实数根9. 如图,在正方形ABCD中,AD=6,点E是边CD上的动点(点E不与端点C,D重合),AE的垂直平分线FG分别交AD,AE,BC于点F,H,G.当 时,DE的长为( )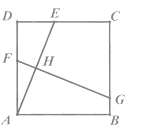 A、2 B、 C、 D、410. 对某个函数给定如下定义:若存在实数M>0,对于任意的函数值y,都满足|y|≤M,则称这个函数是有界函数.在所有满足条件的M中,其中最小值称为这个函数的边界值.现将有界函数 (0 x m,1≤m≤2)的图象向下平移m个单位,得到的函数边界值是t,且 ≤t≤2,则m的取值范围是( )A、1≤m≤ B、 ≤m≤ C、 ≤m≤ D、 ≤m≤2
A、2 B、 C、 D、410. 对某个函数给定如下定义:若存在实数M>0,对于任意的函数值y,都满足|y|≤M,则称这个函数是有界函数.在所有满足条件的M中,其中最小值称为这个函数的边界值.现将有界函数 (0 x m,1≤m≤2)的图象向下平移m个单位,得到的函数边界值是t,且 ≤t≤2,则m的取值范围是( )A、1≤m≤ B、 ≤m≤ C、 ≤m≤ D、 ≤m≤2二、填空题
-
11. 因式分解: = .12. 二次根式 中,字母 的取值范围是 .13. 把抛物线 先向左平移1个单位,再向下平移2个单位,平移后抛物线的表达式是 .
14. 如图是23名射击运动员的一次测试成绩的频数分布折线图,则射击成绩的中位数。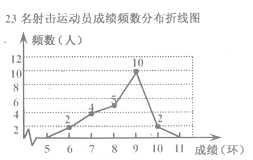 15. 如图,已知点A(2,2)关于直线 (k>0)的对称点恰好落在x轴的正半轴上,则k的值是 .
15. 如图,已知点A(2,2)关于直线 (k>0)的对称点恰好落在x轴的正半轴上,则k的值是 .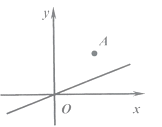 16. 如图,菱形ABCD,∠A=60°,AB=6,点E,F分别是AB,BC边上沿某一方向运动的点,且DE=DF,当点E从A运动到B时,线段EF的中点O运动的路程为 .
16. 如图,菱形ABCD,∠A=60°,AB=6,点E,F分别是AB,BC边上沿某一方向运动的点,且DE=DF,当点E从A运动到B时,线段EF的中点O运动的路程为 .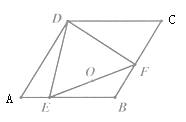
三、解答题
-
17.
(1)、计算: ;(2)、化简:(a+2)(a-2)-a(a-1).18. 解方程: - =0.19. 每年农历五月初五是我国的传统佳节“端午节”,民间历来有吃“粽子”的习俗,我市某食品厂为了解市民对去年销售量较好的栗子粽、豆沙粽、红枣粽、蛋黄粽、大肉粽(以下分别用A,B,C,D,E表示)这五种不同口味粽子的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查结果绘制成如下两幅不完整统计图.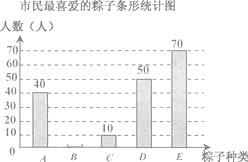

根据以上统计图解答问题:
(1)、本次被调查的市民有多少人,请补全条形统计图;
(2)、扇形统计图中大肉粽对应的圆心角是度;
(3)、若该市有居民约200万人,估计其中喜爱大肉粽的有多少人.
20. 如图,直线 与双曲线y= (k≠0,且 >o)交点A,点A的横坐标为2.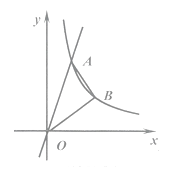 (1)、求点A的坐标及双曲线的解析式;(2)、点B是双曲线上的点,且点B的纵坐标是6,连接OB,AB.求三角形 AOB的面积.21. 如图,是井用手摇抽水机的示意图,支点A的左端是一手柄,右端是一弯钩,点F,A,B始终在同一直线上,支点A距离地面100cm,与手柄端点F之间的距离AF=50cm,与弯钩端点B之间的距离AB=10cm.KT为进水管.
(1)、求点A的坐标及双曲线的解析式;(2)、点B是双曲线上的点,且点B的纵坐标是6,连接OB,AB.求三角形 AOB的面积.21. 如图,是井用手摇抽水机的示意图,支点A的左端是一手柄,右端是一弯钩,点F,A,B始终在同一直线上,支点A距离地面100cm,与手柄端点F之间的距离AF=50cm,与弯钩端点B之间的距离AB=10cm.KT为进水管.
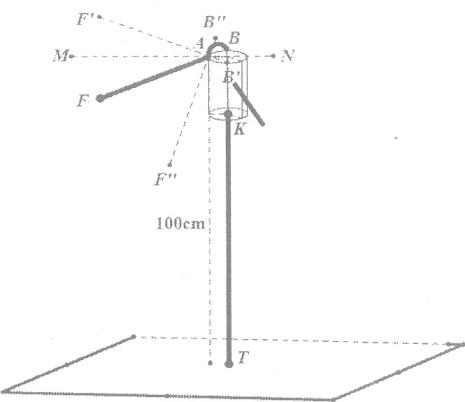 (1)、在一次取水过程中,将手柄AF绕支点A旋转到AF',且与水平线MN的夹角为20°,且此时点B',K,T在一条线上,求点F'离地面的高度.(2)、当不取水时,将手柄绕支点A逆时针旋转90°至点F''位置,求端点F''与进水管KT之间的距离.(忽略进水管的粗细)(参考数据: ≈0.34, ≈0.94, ≈0.36)22. 如图,直线PC交⊙O于A,C两点,AB是⊙O的直径,AD平分∠PAB交⊙O于点D,过D作DE垂直PA,垂足为E.
(1)、在一次取水过程中,将手柄AF绕支点A旋转到AF',且与水平线MN的夹角为20°,且此时点B',K,T在一条线上,求点F'离地面的高度.(2)、当不取水时,将手柄绕支点A逆时针旋转90°至点F''位置,求端点F''与进水管KT之间的距离.(忽略进水管的粗细)(参考数据: ≈0.34, ≈0.94, ≈0.36)22. 如图,直线PC交⊙O于A,C两点,AB是⊙O的直径,AD平分∠PAB交⊙O于点D,过D作DE垂直PA,垂足为E. (1)、求证:DE是⊙O的切线;
(1)、求证:DE是⊙O的切线;
(2)、若AE=1,AC=4,求直径AB的长.
23. 某批发部某一玩具价格如图所示,现有甲、乙两个商店,计划在“六一”儿童节前到该批发部购买此类玩具.两商店所需玩具总数为120个,乙商店所需数量不超过50个,设甲商店购买 个.如果甲、乙两商店分别购买玩具,两商店需付款总和为y元.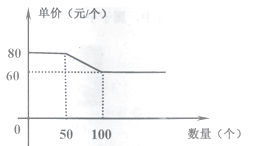 (1)、求y关于 的函数关系式,并写出自变量 的取值范围;(2)、若甲商店购买不超过100个,请说明甲、乙两商店联合购买比分别购买最多可节约多少钱;(3)、“六一”儿童节之后,该批发部对此玩具价格作了如下调整:数量不超过100个时,价格不变;数量超过100个时,每个玩具降价a元.在(2)的条件下,若甲、乙两商店“六一”儿童节之后去批发玩具,最多可节约2800元,求a的值.24. 如图1,两块直角三角纸板(Rt ABC和Rt BDE)按图所示的方式摆放(重合点为B),其中∠BDE=∠ACB= ,∠ABC= ,BD=DE=AC=2.将 BDE绕着点B顺时针旋转.
(1)、求y关于 的函数关系式,并写出自变量 的取值范围;(2)、若甲商店购买不超过100个,请说明甲、乙两商店联合购买比分别购买最多可节约多少钱;(3)、“六一”儿童节之后,该批发部对此玩具价格作了如下调整:数量不超过100个时,价格不变;数量超过100个时,每个玩具降价a元.在(2)的条件下,若甲、乙两商店“六一”儿童节之后去批发玩具,最多可节约2800元,求a的值.24. 如图1,两块直角三角纸板(Rt ABC和Rt BDE)按图所示的方式摆放(重合点为B),其中∠BDE=∠ACB= ,∠ABC= ,BD=DE=AC=2.将 BDE绕着点B顺时针旋转.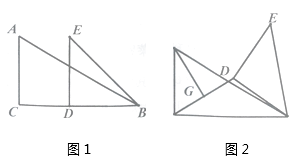 (1)、当点D在BC上时,求CD的长;(2)、当 BDE旋转到A,D,E三点共线时,求 CDE的面积;(3)、如图2,连接CD,点G是CD的中点,连接AG,求AG的最大值和最小值.
(1)、当点D在BC上时,求CD的长;(2)、当 BDE旋转到A,D,E三点共线时,求 CDE的面积;(3)、如图2,连接CD,点G是CD的中点,连接AG,求AG的最大值和最小值.