2017-2018学年北师大版七年级下数学期末模拟试卷(1)
试卷更新日期:2018-06-06 类型:期末考试
一、选择题
-
1. 下列计算的结果是x5的为( )A、x10÷x2 B、x6﹣x C、x2•x3 D、(x2)32. 计算(a﹣1)2正确的是( )A、a2﹣a+1 B、a2﹣2a+1 C、a2﹣2a﹣1 D、a2﹣13. 如图,下列条件中不能判定AB∥CD的是( )
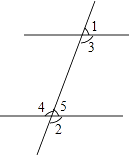 A、∠3=∠4 B、∠1=∠5 C、∠1+∠4=180° D、∠3=∠54.
A、∠3=∠4 B、∠1=∠5 C、∠1+∠4=180° D、∠3=∠54.如图,下列说法中,错误的是( )
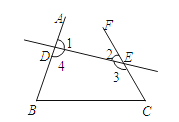 A、∠4与∠B是同位角 B、∠B与∠C是同旁内角 C、∠2与∠C是同位角 D、∠1与∠3是内错角5.
A、∠4与∠B是同位角 B、∠B与∠C是同旁内角 C、∠2与∠C是同位角 D、∠1与∠3是内错角5.梅梅以每件6元的价格购进某商品若干件到市场去销售,销售金额y(元)与销售量x(件)的函数关系图象如图所示,则降价后每件商品的销售利润为( )
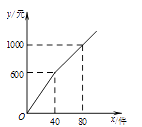 A、4元 B、5元 C、10元 D、15元6. 如图,能判定EB∥AC的条件是( )
A、4元 B、5元 C、10元 D、15元6. 如图,能判定EB∥AC的条件是( ) A、∠A=∠ABE B、∠A=∠EBD C、∠C=∠ABC D、∠C=∠ABE7. 如图,
A、∠A=∠ABE B、∠A=∠EBD C、∠C=∠ABC D、∠C=∠ABE7. 如图,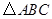 与
与 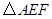 中,
中, 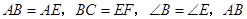 交
交  于
于  .给出下列结论:
.给出下列结论: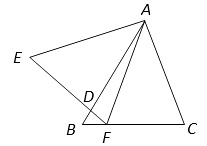
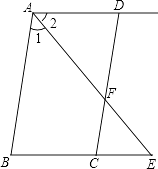
①∠C=∠E;②△ADE∽△FDB;③∠AFE=∠AFC;④FD=FB.其中正确的结论是( ).
A、①③ B、②③ C、①④ D、②④8. 如图,在矩形纸片ABCD中,AB=3,点E在边BC上,将△ABE沿直线AE折叠,点B恰好落在对角线AC上的点F处,若∠EAC=∠ECA,则AC的长是( ) A、 B、6 C、4 D、59. 将一副直角三角板如图放置,使含30°角的三角板的一条直角边和45°角的三角板的一条直角边重叠,则∠1的度数为( )
A、 B、6 C、4 D、59. 将一副直角三角板如图放置,使含30°角的三角板的一条直角边和45°角的三角板的一条直角边重叠,则∠1的度数为( )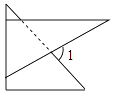 A、45° B、60° C、75° D、85°10. 某学习小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如下的表格,则符合这一结果的实验最有可能的是( )
A、45° B、60° C、75° D、85°10. 某学习小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如下的表格,则符合这一结果的实验最有可能的是( )实验次数
100
200
300
500
800
1000
2000
频率
0.365
0.328
0.330
0.334
0.336
0.332
0.333
A、一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃 B、在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀” C、抛一个质地均匀的正六面体骰子,向上的面点数是5 D、抛一枚硬币,出现反面的概率11. 在一个不透明的袋子里装有3个黑球和若干白球,它们除颜色外都相同.在不允许将球倒出来数的前提下,小明为估计其中白球数,采用如下办法:随机从中摸出一球,记下颜色后放回袋中,充分摇匀后,再随机摸出一球,记下颜色,…不断重复上述过程.小明共摸100次,其中20次摸到黑球.根据上述数据,小明估计口袋中白球大约有()A、10个 B、12 个 C、15 个 D、18个12. 求1+2+22+23…+22012的值,可令S=1+2+22+23+…+22012 , 则2S=2+22+23+24+…+22013 , 因此2S﹣S=22013﹣1,仿照以上推理,计算出1+5+52+53+…+52017的值为( )A、52017﹣1 B、52018﹣1 C、 D、二、填空题
-
13. 袋子中装有除颜色外完全相同的n个黄色乒乓球和3个白色乒乓球,从中随机抽取1个,若选中白色乒乓球的概率是 ,则n的值是 .14. 如果 , ,那么 .15. 如图,AB∥CD,直线EF分别交AB、CD于E、F两点,∠BEF的平分线交CD于点G,若∠EFG=52°,则∠EGF= .
 16. 在△ABC中,∠A=30°,D是AC边上的点;先将△ABC沿着BD翻折,翻折后△ABD的边AB交AC于点E;又将△BCE沿着BE翻折,C点恰好落在BD上,此时∠BEC=78°,则原三角形的∠ABC=度.
16. 在△ABC中,∠A=30°,D是AC边上的点;先将△ABC沿着BD翻折,翻折后△ABD的边AB交AC于点E;又将△BCE沿着BE翻折,C点恰好落在BD上,此时∠BEC=78°,则原三角形的∠ABC=度.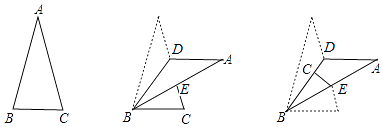
三、解答题
-
17. 计算:(1)、8a2•a4÷a3﹣6a3(2)、(﹣2a﹣3b)(2a﹣3b)18. 先化简,再求值:(2x2+x)﹣[4x2﹣(3x2﹣x)],其中x=﹣ .19.
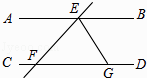
如图所示,已知AB∥DC,AE平分∠BAD,CD与AE相交于点F,∠CFE=∠E.试说明AD∥BC.完成推理过程:
∵AB∥DC(已知)
∴∠1=∠CFE()
∵AE平分∠BAD(已知)
∴∠1=∠2 (角平分线的定义)
∵∠CFE=∠E(已知)
∴∠2=(等量代换)
∴AD∥BC ()
20. 公路上依次有A,B,C三个汽车站,上午8时,小明骑自行车从A,B两站之间距离A站8km处出发,向C站匀速前进,他骑车的速度是每小时16.5km,若A,B两站间的路程是26km,B,C两站的路程是15km.(1)、在小明所走的路程与骑车用去的时间这两个变量中,哪个是自变量?哪个是因变量?(2)、设小明出发x小时后,离A站的路程为y km,请写出y与x之间的关系式.(3)、小明在上午9时是否已经经过了B站?(4)、小明大约在什么时刻能够到达C站?21.如图是一大一小的两个可以自由转动的转盘,甲盘被平均分成6等份,乙盘被平均分成4等份,每个转盘均被涂上红、黄、蓝三种颜色.转动转盘,当转盘停止后,指针指向的颜色即为转出的颜色.小明与小颖参与游戏:小明转动甲盘,小颖转动乙盘.
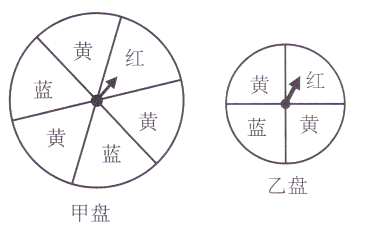 (1)、小明转出的颜色为红色的概率为;(2)、小明转出的颜色为黄色的概率为;(3)、小颖转出的颜色为黄色的概率为;(4)、两人均转动转盘,如果转出的颜色为红,则胜出.你认为该游戏公平吗?为什么?22. 等边△ABC中,点E在AB上,点D在CA的延长线上,且ED=EC.试探索以下问题:
(1)、小明转出的颜色为红色的概率为;(2)、小明转出的颜色为黄色的概率为;(3)、小颖转出的颜色为黄色的概率为;(4)、两人均转动转盘,如果转出的颜色为红,则胜出.你认为该游戏公平吗?为什么?22. 等边△ABC中,点E在AB上,点D在CA的延长线上,且ED=EC.试探索以下问题: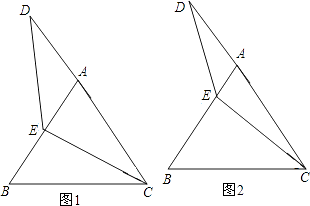 (1)、如图1,当E为AB中点时,试确定线段AD与BE的大小关系,请你直接写出结论:(2)、如图2,若点E为线段AB上任意一点,(1)中结论是否成立,若成立,请证明结论,若不成立,请说明理由。23. 如图1,点P、Q分别是等边△ABC边AB、BC上的动点(端点除外),点P从顶点A、点Q从顶点B同时出发,且它们的运动速度相同,连接AQ、CP交于点M.
(1)、如图1,当E为AB中点时,试确定线段AD与BE的大小关系,请你直接写出结论:(2)、如图2,若点E为线段AB上任意一点,(1)中结论是否成立,若成立,请证明结论,若不成立,请说明理由。23. 如图1,点P、Q分别是等边△ABC边AB、BC上的动点(端点除外),点P从顶点A、点Q从顶点B同时出发,且它们的运动速度相同,连接AQ、CP交于点M.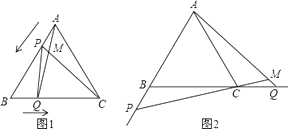 (1)、△ABQ与△CAP全等吗?请说明理由;
(1)、△ABQ与△CAP全等吗?请说明理由;
(2)、当点P、Q分别在AB、BC边上运动时,∠QMC变化吗?若变化,请说明理由;若不变,求出它的度数.(3)、如图2,若点P、Q在运动到终点后继续在AB、BC的延长线上运动,直线AQ、CP交点为M,则∠QMC变化吗?若变化,请说明理由;若不变,则求出它的度数.