广东省佛山市普通高中2018届高三文数教学质量检测试卷(二)
试卷更新日期:2018-06-05 类型:高考模拟
一、单选题
-
1. 已知全集 ,若 , ,则 ( )
A、 B、 C、 D、2. 若复数 满足 ,则 ( )
A、1 B、 C、2 D、33. 已知函数 ,则“ ”是“ ”的( )
A、充分不必要条件 B、必要不充分条件 C、充分必要条件 D、既不充分也不必要条件4. 设 满足约束条件 ,则 的最小值为( )
A、4 B、0 C、2 D、-45. 若抛物线 的焦点在直线 上,则 等于( )A、4 B、0 C、-4 D、-66. 某同学用收集到的 6 组数据对 制作成如图所示的散点图(点旁的数据为该点坐标),并由最小二乘法计算得到回归直线 的方程为 ,相关系数为 .
现给出以下3个结论:
① ; ②直线 恰好过点 ; ③ ;其中正确结论是( )
A、①② B、①③ C、②③ D、①②③7. 执行如图所示的程序框图,当输出的 时,则输入的 的值为( ) A、-2 B、-1 C、 D、8. 如图是一种螺栓的简易三视图,其螺帽俯视图是一个正六边形,则由三视图尺寸,该螺栓的表面积为( )
A、-2 B、-1 C、 D、8. 如图是一种螺栓的简易三视图,其螺帽俯视图是一个正六边形,则由三视图尺寸,该螺栓的表面积为( ) A、 B、 C、 D、9. 甲乙丙丁四个人背后各有 1个号码,赵同学说:甲是2号,乙是3号;钱同学说:丙是2号,乙是4号;孙同学说:丁是2号,丙是3号;李同学说:丁是1号,乙是3号.他们每人都说对了一半,则丙是( )
A、 B、 C、 D、9. 甲乙丙丁四个人背后各有 1个号码,赵同学说:甲是2号,乙是3号;钱同学说:丙是2号,乙是4号;孙同学说:丁是2号,丙是3号;李同学说:丁是1号,乙是3号.他们每人都说对了一半,则丙是( )
A、1号 B、2号 C、3号 D、4号10. 已知双曲线 的左焦点为 ,右顶点为 ,虚轴的一个端点为 ,若 为等腰三角形,则该双曲线的离心率为( )A、 B、 C、 D、11. 已知函数 的图象在区间 上不单调,则 的取值范围为( )A、 B、 C、 D、12. 已知函数 ,曲线 关于直线 对称,现给出如结论:①若 ,则存在 ,使 ;②若 ,则不等式 的解集为 ;③若 ,且 是曲线 的一条切线,则 的取值范围是 .其中正确结论的个数为( )
A、0 B、1 C、2 D、3二、填空题
-
13. 曲线 在点 处的切线方程为 .
14. 若 ,则 .
15. 直角 中, 为 中点, 在斜边 上,若 ,则 .
16. 数列 满足 .则 .
三、解答题
-
17. 如图,在平面四边形 中, .
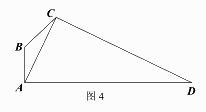
(Ⅰ)若 ,求 ;
(Ⅱ)若 ,求 .
18. 如图,在多面体 中,四边形 是梯形, , 平面 ,平面 ⊥平面 .
(Ⅰ)求证: 平面 ;
(Ⅱ)若 是等边三角形, ,求多面体 的体积.
19. 从某企业生产的产品的生产线上随机抽取 件产品,测量这批产品的一项质量指标值,由测量结果得如图所示的频率分布直方图:
(Ⅰ) 估计这批产品质量指标值的样本平均数 和样本方差 (同一组中的数据用该组区间的中点值作代表);
(Ⅱ) 若该种产品的等级及相应等级产品的利润(每件)参照以下规则(其中 为产品质量指标值):
当 , 该产品定为一等品,企业可获利 200 元;
当 且 ,该产品定为二等品,企业可获利 100 元;
当 且 ,该产品定为三等品,企业将损失 500 元;
否则该产品定为不合格品,企业将损失 1000 元.
(ⅰ)若测得一箱产品(5 件)的质量指标数据分别为:76、85、93、105、112,求该箱产品的利润;
(ⅱ)设事件 ;事件 ;事件 . 根据经验,对于该生产线上的产品,事件 发生的概率分别为0.6826、0.9544、0.9974.根据以上信息,若产品预计年产量为10000件,试估计该产品年获利情况.(参考数据: )
20. 已知直线 过点 ,且与抛物线 相交于 两点,与 轴交于点 ,其中点 在第四象限, 为坐标原点.(Ⅰ)当 是 中点时,求直线 的方程;
(Ⅱ)以 为直径的圆交直线 于点 ,求 的值.
21. 已知 ,函数 .(Ⅰ)若 有极小值且极小值为0 ,求 的值;
(Ⅱ)当 时, , 求 的取值范围.