2015-2016学年浙江省嘉兴市高二上学期期末数学试卷

试卷更新日期：2017-01-04 类型：期末考试

进入出卷网下载

一、选择题

1. 不等式x²+2x﹣3＞0的解集是（）

A、{x|x＜﹣3或x＞1} B、{x|x＜﹣1或x＞3} C、{x|﹣1＜x＜3} D、{x|﹣3＜x＜1}

查看试题解析
2. 命题“若x＜3，则x²≤9”的逆否命题是（）

A、若x≥3，则x²＞9 B、若x²≤9，则x＜3 C、若x²＞9，则x≥3 D、若x²≥9，则x＞3

查看试题解析
3. 若a，b是任意的实数，且a＞b，则（）

A、|a|＞|b| B、 $\frac{b}{a} < 1$ C、lga＜lgb D、 ${(\frac{1}{2})}^{a} < {(\frac{1}{2})}^{b}$

查看试题解析
4. 已知点A（0，0，0），B（1，0，1），C（0，1，1），则平面ABC的一个法向量 $\vec{m}$ 是（）

A、（1，1，1） B、（1，1，﹣1） C、（﹣1，1，1） D、（1，﹣1，1）

查看试题解析
5. 已知a，b，c是实数，则“a≥b”是“ac²≥bc²”的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
6. 如图，记正方形ABCD四条边的中点为S，M，N，T，连接四个中点得小正方形SMNT．将正方形ABCD，正方形SMNT绕对角线AC旋转一周得到的两个旋转体的体积依次记为V₁ ， V₂ ，则V₁：V₂=（）

A、8：1 B、2：1 C、4：3 D、8：3

查看试题解析
7. 设a，b，c是三条不同的直线，α，β，γ是三个不同的平面，已知α∩β=a，α∩γ=b，β∩γ=c，下列四个命题中不一定成立的是（）

A、若a、b相交，则a、b、c三线共点 B、若a、b平行，则a、b、c两两平行 C、若a、b垂直，则a、b、c两两垂直 D、若α⊥γ，β⊥γ，则a⊥γ

查看试题解析
8. 如图，在四棱锥A﹣BCD中，△ABD，△BCD均为正三角形，且平面ABD⊥平面BCD，点O，M分别为棱BD，AC的中点，则异面直线AB与OM所成角的余弦值为（）

A、 $\frac{\sqrt{6}}{4}$ B、 $\frac{\sqrt{3}}{2}$ C、 $\frac{\sqrt{3}}{3}$ D、 $\frac{\sqrt{2} + \sqrt{6}}{4}$

查看试题解析
9. 若实数x、y满足xy＞0，则 $\frac{x}{x + y}$ + $\frac{2 y}{x + 2 y}$ 的最大值为（）

A、2﹣ $\sqrt{2}$ B、2+ $\sqrt{2}$ C、4-2 $\sqrt{2}$ D、4+2 $\sqrt{2}$

查看试题解析
10. 如图，底面为正方形且各侧棱长均相等的四棱锥V﹣ABCD可绕着棱AB任意旋转，若AB⊂平面α，M，N分别是AB，CD的中点，AB=2，VA= $\sqrt{5}$ ，点V在平面α上的射影为点O，则当ON的最大时，二面角C﹣AB﹣O的大小是（）

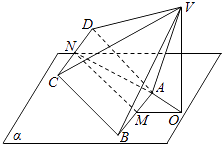A、90° B、105° C、120° D、135°

查看试题解析

二、填空题

11. 已知 $\vec{a} = (1 ， 0 ， 1)$ ， $\vec{b} = (t ， 1 ， 1)$ ， $\vec{a} ⊥ \vec{b}$ ，则t= ．

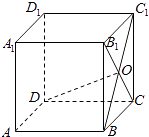
查看试题解析
12. 已知圆锥的侧面展开图是一个半径为2的半圆，则这个圆锥的高是．

查看试题解析
13. 已知集合A={x|（ax﹣1）（3x+1）＞0}= ${x | - \frac{1}{3} < x < \frac{1}{a}}$ ，则a的取值范围是．

查看试题解析
14. 如图，在正方体ABCD﹣A₁B₁C₁D₁中，B₁C和BC₁相交于点O，若 $\vec{D O} = x \vec{D A} + y \vec{D C} + z \vec{D D_{1}}$ ，则 $\frac{x}{y}$ =

查看试题解析
15. 某几何体的三视图如图所示，则此几何体的表面积是．

查看试题解析
16. 已知 $i ， j ， k$ 为两两垂直的单位向量， $\vec{A B} = 2 i + 4 j - k$ ， $\vec{A C} = 2 i + j + k$ ，则 $\vec{A B}$ 与 $\vec{A C}$ 夹角的余弦值为．

查看试题解析
17. 已知实数x，y满足x²+4y²﹣2xy=4，则x+2y的最大值是．

查看试题解析
18. 如图，在三棱柱A₁B₁C₁﹣A₂B₂C₂中，各侧棱均垂直于底面，∠A₁B₁C₁=90°，A₁B₁=B₁C₁=3，C₁M=2B₁N=2，则直线B₁C₁与平面A₁MN所成角的正弦值为．

查看试题解析

三、解答题

19. 解下列不等式：

(1)、|2x﹣1|＜x；

(2)、|2x﹣3|+|x﹣1|≥5．

查看试题解析
20. 已知m＞0，n＞0，x=m+n，y= $\frac{1}{m} + \frac{16}{n}$ ．

(1)、求xy的最小值；

(2)、若2x+y=15，求x的取值范围．

查看试题解析
21. 已知四棱锥P﹣ABCD的底面是菱形，PA⊥面ABCD，PA=AD=2，∠ABC=60°，E为PD中点．

(1)、求证：PB∥平面ACE；

(2)、求二面角E﹣AC﹣D的正切值．

查看试题解析
22. 在梯形ABCD中，AD∥BC，∠ABC=90°，点M、N分别在边AB、BC上，沿直线MD、DN、NM，分别将△AMD、△CDN、△BNM折起，点A，B，C重合于一点P．

(1)、证明：平面PMD⊥平面PND；

(2)、若cos∠DNP= $\frac{3}{5}$ ，PD=5，求直线PD与平面DMN所成角的正弦值．

查看试题解析