2015-2016学年浙江省温州市平阳县七年级上学期期末数学试卷

试卷更新日期：2017-01-03 类型：期末考试

进入出卷网下载

一、选择题

1. 给出四个数0， $\sqrt{2}$ ， $\frac{1}{3}$ ，﹣1，其中最小的数是（）

A、0 B、 $\sqrt{2}$ C、 $\frac{1}{3}$ D、﹣1

查看试题解析
2. 如图，把原来弯曲的河道改直，A，B两地间的河道长度变短，这样做的道理是（　　）

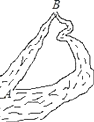A、两点确定一条直线 B、两点之间线段最短 C、两点之间直线最短 D、垂线段最短

查看试题解析
3. 下列各数0， $- \sqrt[3]{9}$ ， $\frac{\sqrt{3}}{5}$ ， $\sqrt{4}$ ， $\frac{5}{7}$ ，﹣3.14，2π中，是无理数的有（）

A、5个 B、4个 C、个 D、2个

查看试题解析
4. 下列计算正确的是（　　）

A、3a+4b=7ab B、7a﹣3a=4 C、3a+a=3a² D、3a²b﹣4a²b=﹣a²b

查看试题解析
5. 有长为l的篱笆，利用他和房屋的一面墙围成如图形状的长方形园子，园子的宽为t，则所围成的园子面积为（）

A、（1﹣2t）t B、（1﹣t）t C、（ $\frac{1}{2}$ ﹣t）t D、（1﹣ $\frac{t}{2}$ ）t

查看试题解析
6. 下列说法正确的是（）

A、若AB=2AC，则点C是线段AB的中点 B、一条射线把一个角分成两个角，这条射线是这个角的平分线 C、点到直线的距离是指从直线外一点到这条直线的垂线的长度 D、在同一平面内，过一点有一条而且仅有一条直线垂直于已知直线

查看试题解析
7. x、y、z在数轴上的位置如图所示，则化简|x﹣y|+|z﹣y|的结果是（）

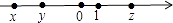A、x+z﹣2y B、2y﹣x﹣z C、z﹣x D、x﹣z

查看试题解析
8. 将正整数按如图所示的位置顺序排列：
根据排列规律，则2015应在（　　）

A、A处 B、B处 C、C处 D、D处

查看试题解析

二、填空题

9. ﹣ $\frac{1}{3}$ 的相反数是

查看试题解析
10. 化简： $\sqrt{9}$ = ．

查看试题解析
11. 一台电视机的原价是2000元，若按原价的八折出售，则购买a台这样的电视机需要元．

查看试题解析
12. 已知x=﹣2是关于x的方程3+ax=x的解，则a的值为

查看试题解析
13. 已知∠α=47°30′，则∠α的余角的度数为°．

查看试题解析
14. 已知|3m﹣12|+ ${(\frac{n}{2} + 1)}^{2}$ =0，则2m﹣n= ．

查看试题解析
15. 如图，将三角形ABC纸片沿MN折叠，使点A落在点A′处，若∠A′MB=55°，则∠AMN=°．

查看试题解析
16. 已知x﹣3y=2，则代数式5﹣3x+9y的值为

查看试题解析
17. 已知关于x的方程kx=5﹣x，有正整数解，则整数k的值为．

查看试题解析
18. 小明和小慧两位同学在数学活动课中，把长为30cm，宽为10cm的长方形白纸条粘合起来，小明按如图甲所示的方法粘合起来得到长方形ABCD，粘合部分的长度为6cm，小慧按如图乙所示的方法粘合起来得到长方形A₁B₁C₁D₁ ，黏合部分的长度为4cm．若长为30cm，宽为10cm的长方形白纸条共有100张，则小明应分配到张长方形白纸条，才能使小明和小慧按各自要求黏合起来的长方形面积相等（要求100张长方形白纸条全部用完）．

查看试题解析

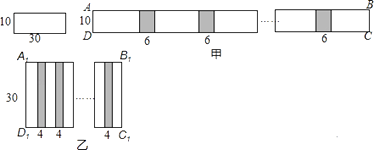
三、解答题

19. 计算：

(1)、﹣47×（﹣ $\frac{1}{4}$ ）+53× $\frac{1}{4}$

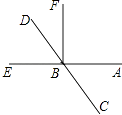
(2)、2²+|﹣6|+ $\sqrt[3]{- \frac{27}{8}}$ ﹣（﹣1）²⁰¹⁵ ．

查看试题解析
20. 解方程：

(1)、2x﹣（x+10）=6x

(2)、1﹣ $\frac{3 x - 5}{2} = \frac{1 + 5 x}{3}$ ．

查看试题解析
21. 先化简，再求值：2（a²+3ab﹣4.5）﹣（a²﹣6ab﹣9），其中a=﹣5，b= $\frac{3}{4}$ ．

查看试题解析
22. 如图，直线AE与CD相交于点B，∠DBE=50°，BF⊥AE，求∠CBF和∠DBF的度数．

查看试题解析
23. 为给同学们创造更好的读书条件，学校准备新建一个长度为L的度数长廊，并准备用若干块带有花纹和没有花纹的两种规格、大小相同的正方形地面砖搭配在一起，按如图所示的规律拼成图案铺满长廊，已知每个小正方形地面砖的边长均为0.6m．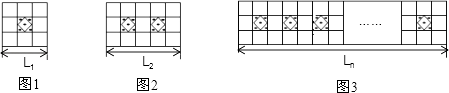

(1)、按图示规律，第一图案的长度L₁=m；第二个图案的长度L₂=m．

(2)、请用代数式表示带有花纹的地面砖块数n与走廊的长度L_n之间的关系．

(3)、当走廊的长度L为36.6m时，请计算出所需带有花纹图案的瓷砖的块数．

查看试题解析
24. 如图，直线l上有A、B两点，AB=24cm，点O是线段AB上的一点，OA=2OB．

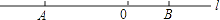(1)、OA=cm，OB=cm．

(2)、若点C是线段AO上一点，且满足AC=CO+CB，求CO的长．

(3)、若动点P、Q分别从A、B同时出发，向右运动，点P的速度为2cm/s，点Q的速度为1cm/s，设运动时间为t（s），当点P与点Q重合时，P、Q两点停止运动．
①当t为何值时，2OP﹣OQ=8．
②当点P经过点O时，动点M从点O出发，以3cm/s的速度也向右运动．当点M追上点Q后立即返回，以同样的速度向点P运动，遇到点P后立即返回，又以同样的速度向点Q运动，如此往返，直到点P、Q停止时，点M也停止运动．在此过程中，点M行驶的总路程为 cm．

查看试题解析